Lý thuyết, bài tập Góc tạo bởi tiếp tuyến và dây cung đầy đủ có lời giải

Tài liệu Bài tập Góc tạo bởi tiếp tuyến và dây cung gồm các nội dung chính sau:

I. Phương pháp giải

– tóm tắt lý thuyết ngắn gọn.

II. Bài tập

– gồm 10 bài tập vận dụng có đáp án và lời giải chi tiết giúp học sinh tự rèn luyện cách giải các dạng Bài tập Góc tạo bởi tiếp tuyến và dây cung.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

Bài tập Góc tạo bởi tiếp tuyến và dây cung (ảnh 1)

BÀI TẬP GÓC TẠO BỞI TIẾP TUYẾN VÀ DÂY CUNG

I. Phương pháp giải

1.Khái niệm góc tạo bởi tia tiếp tuyến

và dây cung

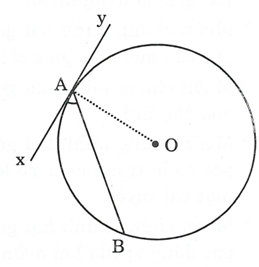Bài tập Góc tạo bởi tiếp tuyến và dây cung (ảnh 2) Hình bên , xy là tiếp tuyến của đường tròn

(O) tại A, tiếp tuyến A là gốc chung của

hai tia đối nhau. Mỗi tia đó là một tia tiếp tuyến.

Góc BAx có đỉnh A nằm trên đường tròn,

cạnh Ax là một tia tiếp tuyến còn cạnh kia

chứa dây cung AB

Ta gọi góc BAx là góc tạo bởi một tia tiếp tuyến và dây cung

2.Định lí

Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn

3.Hệ quả

Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau

II. Bài tập

Bài 1: (27/79/SGK T2)

Cho đường tròn (O), đường kính AB, lấy điểm P khác A và B trên đường tròn. Gọi T là giao điểm của AP với tiếp tuyến tại B của đường tròn.

Chứng minh $\hat{A P O} = \hat{P B T}$

Giải

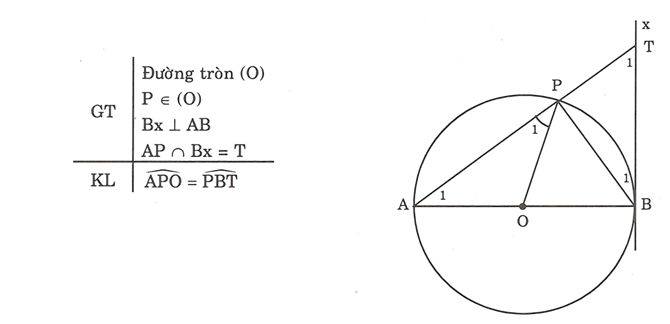
Chứng minh

Bài này thuộc thể loại toán chứng minh hai góc bằng nhau

Muốn chứng minh hai góc bằng nhau có nhiều cách

*Muốn chứng minh hai góc bằng nhau ta chứng minh hai tam giác chứa hai góc đó bằng nhau

*Muốn chứng minh hai góc bằng nhau ta chứng minh hai góc đó là hai góc của một tam giác cân

*Muốn chứng minh hai góc bằng nhau ta chứng minh hai góc đó là hai góc đối đỉnh

*Muốn chứng minh hai góc bằng nhau ta chứng minh hai góc đó là hai góc so le trong hoặc so le ngoài tạo bởi hai đường thẳng song song với một cát tuyến

*Muốn chứng minh hai góc bằng nhau ta chứng minh hai góc đó là hai góc đồng vị của hai đường thẳng song song với một cát tuyến

* Muốn chứng minh hai góc bằng nhau ta chứng minh hai góc đó cùng bù (hoặc cùng phụ) với một góc thứ ba

* Muốn chứng minh hai góc bằng nhau ta chứng minh hai góc đó là hai góc đối đỉnh của một hình bình hành

Muốn chứng minh hai góc bằng nhau ta chứng minh hai góc đó là hai góc nội tiếp cùng chắn một cung (hoặc chắn hai cung bằng nhau) của một đường tròn v.v…với giả thiết “tiếp tuyến” “đường kính” ta chứng minh thông qua góc cùng phụ

Do $B x ⊥ A B$ (vì Bx là tiếp tuyến của (O) tại B) $\Rightarrow Δ A B T$ vuông tại $B \Rightarrow \hat{A_{1}} + \hat{T_{1}} = 90 °$ (theo định lí: Trong một tam giác vuông hai góc nhọn phụ nhau) (1)

Do AB là đường kính $\hat{A P B} = 90 °$ (góc nội tiếp chắn nửa đường tròn) $\Rightarrow \hat{B P T} = 90 °$ (kề bù với ) $\hat{A P B} = 90 °$ $\Rightarrow Δ B P T$ vuông tại P

$\Rightarrow \hat{B_{1}} + \hat{T_{1}} = 90 °$ (2)

Từ (1) và (2) có $\hat{B_{1}} = \hat{T_{1}}$ (3)

$Δ A O P$ có $O A = O P$ (hai bán kính của một đường tròn) $\Rightarrow Δ A O P$ cân tại O (tam giác có hai cạnh bằng nhau là tam giác cân)

$\Rightarrow \hat{A_{1}} = \hat{P_{1}}$ (4)

Từ (1) và (4) ta có $\hat{P_{1}} + \hat{T_{1}} = 90 °$ (5)

Từ (2) và (5) ta có $\hat{P_{1}} = \hat{B_{1}}$ (cùng phụ với $\hat{T_{1}}$ )

Vậy $\hat{A P O} = \hat{P B T}$

Xem thêm

Bài liên quan:

Leave a Comment Hủy