SBT Toán 9 Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp | Giải SBT Toán lớp 9

Giải SBT Toán 9 Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp

Bài 44 trang 107 SBT Toán 9 tập 2: Vẽ hình vuông $A B C D$ tâm $O$ rồi vẽ tam giác đều có một đỉnh là $A$ và nhận $O$ làm tâm. Nêu cách vẽ.
Phương pháp giải:

Ta sử dụng kiến thức:

+) Hình vuông là có hai đường chéo bằng nhau, cắt nhau tại trung điểm mỗi đường, và hai đường chéo vuông góc với nhau.

+) Tam giác đều có các cạnh, các góc bằng nhau bằng $60^{\circ} .$

+) Bất kì đa giác nào cũng có một và chỉ một đường tròn ngoại tiếp.

Lời giải:

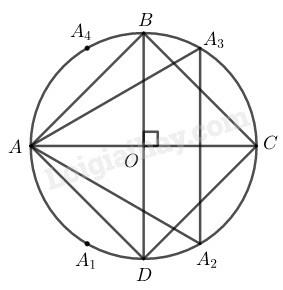
SBT Toán 9 Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp | Giải SBT Toán lớp 9 (ảnh 1)

Cách vẽ:

− Vẽ đường tròn $(O; R)$

− Kẻ $2$ đường kính $A C ⊥ B D$

− Nối $A B, B C, C D, D A$ ta được tứ giác $A B C D$ là hình vuông nội tiếp trong đường tròn $(O; R)$

− Từ $A$ đặt liên tiếp các cung bằng nhau có dây tương ứng bằng bán kính $R$ là:

$\overset{⏜}{A A_{1}},$ $\overset{⏜}{A_{1} A_{2}},$ $\overset{⏜}{A_{2} C},$ $\overset{⏜}{C A_{3}},$ $\overset{⏜}{A_{3} A_{4}}$

Nối $A A_{2},$ $A_{2} A_{3},$ $A_{3} A,$ ta có $∆ A A_{2} A_{3},$ là tam giác đều nhận $O$ làm tâm.

Chứng minh:

Vì các cung $\overset{⏜}{A A_{1}},$ $\overset{⏜}{A_{1} A_{2}},$ $\overset{⏜}{A_{2} C},$ $\overset{⏜}{C A_{3}},$ $\overset{⏜}{A_{3} A_{4}}$ bằng nhau nên ta có:

$\overset{⏜}{A A_{2}}$ $= \overset{⏜}{A_{2} A_{3}}$ $= \overset{⏜}{A_{3} A}$

Suy ra $A A_{2} = A_{2} A_{3} = A_{3} A$ nên tam giác $A A_{2} A_{3}$ là tam giác đều

Theo cách vẽ ta có $O$ là tâm đường tròn ngoại tiếp tam giác $A A_{2} A_{3}$

Vậy tam giác $A A_{2} A_{3}$ thỏa mãn đề bài.

Bài 45 trang 107 SBT Toán 9 tập 2: Vẽ đường tròn tâm $O$ bán kính $R = 2 c m$ rồi vẽ hình tám cạnh đều nội tiếp đường tròn $(O; 2 c m) .$ Nêu cách vẽ.
Phương pháp giải:

Ta sử dụng kiến thức:

+) Tất cả các đỉnh của đa giác đều đều nằm trên một đường tròn. Tất cả các đa giác đều đều có một đường tròn ngoại tiếp.

Lời giải:

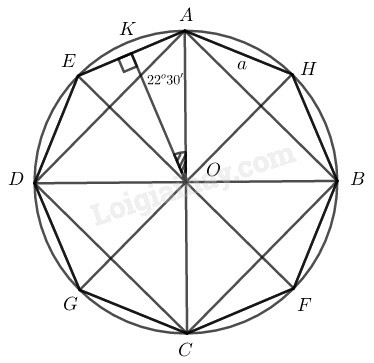
SBT Toán 9 Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp | Giải SBT Toán lớp 9 (ảnh 2)

Cách vẽ:

− Vẽ đường tròn $(0; 2 c m)$

− Vẽ đường kính $A C ⊥ B D$

− Nối $A B, B C, C D, D A$ ta có hình vuông $A B C D$ nội tiếp đường tròn $(0; 2 c m)$

− Kẻ đường kính $E F ⊥ A D;$ đường kính $G H ⊥ A B$

Nối $A E, E D, D G, G C, C F,$ $F B,$ $B H,$ $H A$ ta có đa giác $A E D G C F B H$ là đa giác đều $8$ cạnh nội tiếp trong đường tròn $(0; 2 c m) .$

Bài 46 trang 107 SBT Toán 9 tập 2: Cho một đa giác đều $n$ cạnh có độ dài mỗi cạnh là $a .$ Hãy tính bán kính $R$ của đường tròn ngoại tiếp và bán kính $r$ của đường tròn nội tiếp đa giác đều đó.

Hướng dẫn:

Tính $\hat{C O B}$ rồi tính $\sin \hat{C O B}$ và $\tan \hat{C O B},$ từ đây tính được $R$ và $r$ $(h .4) .$

Phương pháp giải:

Ta sử dụng kiến thức:

+) Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác.

+) Đường tròn tiếp xúc với tất cả các cạnh của đa giác được gọi là đường tròn nội tiếp đa giác.

+) Số đo góc ở tâm chắn mỗi cạnh của đa giác đều $n$ cạnh bằng $\frac{360^{\circ}}{n} .$

Lời giải:

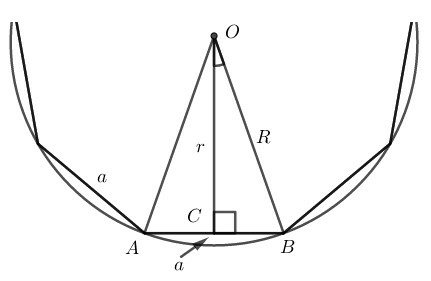
SBT Toán 9 Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp | Giải SBT Toán lớp 9 (ảnh 3)

Giả sử một đa giác đều $n$ cạnh có độ dài một cạnh là $a .$ Gọi $R$ là bán kính đường tròn ngoại tiếp, $r$ bán kính đường tròn nội tiếp.

$\Rightarrow O B = R; O C = r$

$\hat{A O B} = \frac{360^{\circ}}{n}$

$\Rightarrow \hat{C O B} = \frac{360^{\circ}}{n} : 2 = \frac{180^{\circ}}{n}$

Trong $∆ O C B$ ta có: $\hat{O C B} = 90^{\circ}$

Nên $\sin \hat{C O B} = \frac{C B}{O B} = \frac{\frac{a}{2}}{R} = \frac{a}{2 R}$

$\Rightarrow 2 R = \frac{a}{\sin \frac{180^{\circ}}{n}}$

$\Rightarrow R = \frac{a}{2 \sin \frac{180^{\circ}}{n}}$

Xét tam giác $O C B$ vuông tại $C$ , ta có:

$\tan \hat{C O B} = \frac{C B}{O C} = \frac{\frac{a}{2}}{r} = \frac{a}{2 r}$

$\Rightarrow 2 r = \frac{a}{\tan \frac{180^{\circ}}{n}}$

$\Rightarrow r = \frac{a}{2 \tan \frac{180^{\circ}}{n}}$

Bài 47 trang 108 SBT Toán 9 tập 2:

$a)$ Vẽ một lục giác đều $A B C D E G$ nội tiếp đường tròn bán kính $2 c m$ rồi vẽ hình $12$ cạnh đều $A I B J C K D L E M G N$ nội tiếp đường tròn đó. Nêu cách vẽ.

$b)$ Tính độ dài cạnh $A I .$

$c)$ Tính bán kính $r$ của đường tròn nội tiếp hình $A I B J C K D L E M G N .$

Hướng dẫn. Áp dụng các công thức ở bài $46.$

Phương pháp giải:

Ta sử dụng kiến thức:

+) Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác.

+) Đường tròn tiếp xúc với tất cả các cạnh của đa giác được gọi là đường tròn nội tiếp đa giác.

+) Số đo góc ở tâm chắn mỗi cạnh của đa giác đều $n$ cạnh bằng $\frac{360^{\circ}}{n} .$

Lời giải:

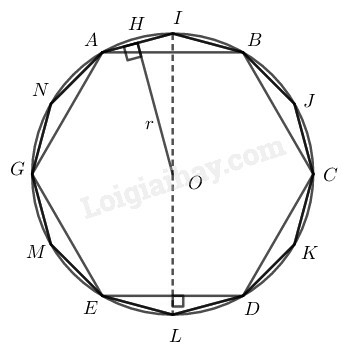
SBT Toán 9 Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp | Giải SBT Toán lớp 9 (ảnh 4)

$a)$ Cách vẽ:

− Vẽ đường tròn $(0; 2 c m)$

− Từ điểm $A$ trên đường tròn $(0; 2 c m)$ đặt liên tiếp các cung bằng nhau có dây căng cung $2 c m .$

$\overset{⏜}{A B}$ $= \overset{⏜}{B C}$ $= \overset{⏜}{C D}$ $= \overset{⏜}{D E}$ $= \overset{⏜}{E G}$

Nối $A B, B C, C D, D E, E G, G A$ ta có lục giác đều $A B C D E G$ nội tiếp trong đường tròn $(0; 2 c m) .$

− Kẻ đường kính vuông góc với $A B$ và $D E$ cắt đường tròn tại $I$ và $L .$

Ta có: $\overset{⏜}{A I} = \overset{⏜}{I B};$ $\overset{⏜}{L D} = \overset{⏜}{L E}$

− Kẻ đường kính vuông góc với $B C$ và $E G$ cắt đường tròn tại $J$ và $M .$

$\overset{⏜}{B J} = \overset{⏜}{J C}$ ; $\overset{⏜}{M E} = \overset{⏜}{M G}$

− Kẻ đường kính vuông góc với $C D$ và $A G$ cắt đường tròn tại $N$ và $K .$

$\overset{⏜}{K C} = \overset{⏜}{K D};$ $\overset{⏜}{N A} = \overset{⏜}{N G}$

Nối $A I, I B, B J, J C, C K, K D, D L,$ $L E,$ $E M,$ $M G,$ $G N,$ $N A$

Ta có đa giác đều $12$ cạnh $A I B J C K D L E M G N .$

$b)$ $A I$ là cạnh của đa giác đều $12$ cạnh.

Kẻ $O H ⊥ A I$

$\hat{I O H} = \frac{180^{\circ}}{12} = 15^{\circ}$

Xét tam giác vuông $I O H$ có: $O I = \frac{H I}{\sin \hat{I O H}}$

$\Rightarrow O I = \frac{A I}{2 \sin \hat{I O H}}$

$\Rightarrow A I = O I .2 \sin \hat{I O H}$

$A I = 2. 2 s i n 15^{\circ} \approx$ $1, 04 (c m)$

$c)$ $O H = r$ bán kính đường tròn nội tiếp đa giác đều $12$ cạnh.

Trong tam giác vuông $O H I$ ta có $O H = O I . c o s \hat{H O I} = 2. c {o s 15}^{\circ} \approx 1, 93 (c m)$

Bài 48 trang 108 SBT Toán 9 tập 2:

$a)$ Tính cạnh của một ngũ giác đều nội tiếp đường tròn bán kính $3 c m .$

$b)$ Tính cạnh của một ngũ giác đều ngoại tiếp đường tròn bán kính $3 c m .$

Phương pháp giải:

Ta sử dụng kiến thức:

+) Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác.

+) Đường tròn tiếp xúc với tất cả các cạnh của đa giác được gọi là đường tròn nội tiếp đa giác.

+) Số đo góc ở tâm chắn mỗi cạnh của đa giác đều $n$ cạnh bằng $\frac{360^{\circ}}{n} .$

Lời giải:

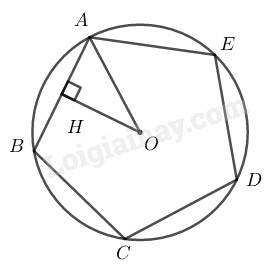
SBT Toán 9 Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp | Giải SBT Toán lớp 9 (ảnh 5)

$a)$ Kẻ $O H ⊥ A B,$ ta có: $H A = H B = \frac{1}{2} A B, O A = R = 3 c m$

Vì $A B C D E$ là ngũ giác đều nên: $\hat{B O A} = \frac{360^{\circ}}{5} = 72^{\circ}$

Suy ra $\hat{H O A} = \frac{\hat{B O A}}{2}$ $= \frac{72^{\circ}}{5} = 36^{\circ}$

Trong tam giác vuông $O H A$ vuông tại $H$ ta có:

$A H = O A . \sin \hat{H O A}$

$\Rightarrow A B = 2. A H = 2 O A . \sin \hat{H O A}$ $= 2.3. \sin 36^{\circ} \approx 3, 522$ $(c m)$

$b)$ Từ giả thiết suy ra $O H = r = 3 c m$

Trong tam giác vuông $O H A$ vuông tại $H$ ta có:

$A H = O H . \tan \hat{H O A}$ $\Rightarrow A B = 2. A H = 2. O H . \tan \hat{H O A}$ $= 2.3. \tan 36^{\circ} \approx 4, 356$ $(c m)$

Bài 49 trang 108 SBT Toán 9 tập 2: Tính cạnh của hình tám cạnh đều theo bán kính $R$ của đường tròn ngoại tiếp.

Hướng dẫn:

Cách $1 :$ áp dụng công thức $a = 2 R \sin \frac{180^{\circ}}{n}$

Cách $2 :$ tính trực tiếp.

Vẽ dây $A B$ là cạnh của một hình vuông nội tiếp đường tròn $(O),$ gọi $C$ là điểm chính giữa của cung nhỏ $A B .$ Khi đó $C A$ là cạnh của hình tám cạnh đều nội tiếp. Hãy tính $C A$ trong tam giác vuông $C A C^{'} .$

Phương pháp giải:

Ta sử dụng kiến thức:

+) Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác.

+) Đường tròn tiếp xúc với tất cả các cạnh của đa giác được gọi là đường tròn nội tiếp đa giác.

+) Trong tam giác vuông, bình phương cạnh góc vuông bằng tích cạnh huyền với hình chiếu của cạnh góc vuông đó trên cạnh huyền.

Lời giải:

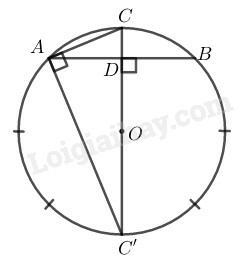
SBT Toán 9 Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp | Giải SBT Toán lớp 9 (ảnh 6)

Cách $1 :$ Áp dụng công thức $a = 2 R \sin \frac{180^{\circ}}{n},$ ta có:

$a = 2 R \sin 22^{\circ} 30^{'}$ $\approx 0, 765 R$

Cách $2 :$

$A C$ là cạnh của đa giác đều $8$ cạnh.

Nên $s đ \overset{⏜}{A C} = \frac{1}{8} {.360}^{0} = 45^{0}$

Do đó $\hat{A C^{'} C} = \frac{s đ \overset{⏜}{A C}}{2} = 22^{0} 30^{'}$ (tính chất góc nội tiếp)

Trong tam giác vuông $C A C^{'},$ ta có:

$\sin \hat{A C^{'} C} = \frac{A C}{C C^{'}}$

$\Rightarrow A C = C C^{'} . \sin \hat{A C^{'} C}$ $= 2 R . \sin 22^{0} 30^{'} \approx 0, 765 R$

Bài 50 trang 108 SBT Toán 9 tập 2: Trong đường tròn $(O; R)$ cho một dây $A B$ bằng cạnh hình vuông nội tiếp và dây $B C$ bằng cạnh tam giác đều nội tiếp (điểm $C$ và điểm $A$ ở cùng một phía đối với $B O$ ). Tính các cạnh của tam giác $A B C$ và đường cao $A H$ của nó theo $R .$
Phương pháp giải:

Ta sử dụng kiến thức:

+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.

+) Nếu $C$ là một điểm trên cung $A B$ thì: $s đ \overset{⏜}{A B} = s đ \overset{⏜}{A C} + s đ \overset{⏜}{C B} .$

Lời giải:

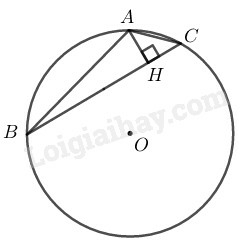
SBT Toán 9 Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp | Giải SBT Toán lớp 9 (ảnh 7)

Dây $A B$ bằng cạnh hình vuông nội tiếp đường tròn $(O; R)$ nên $A B = R \sqrt{2}$ và cung $\overset{⏜}{A B}$ nhỏ có $s đ \overset{⏜}{A B} = 360^{0} : 4 = 90^{\circ}$ .

Dây $B C$ bằng cạnh hình tam giác đều nội tiếp đường tròn $(O; R)$ nên $B C = R \sqrt{3}$ và cung nhỏ $\overset{⏜}{B C}$ có $s đ \overset{⏜}{B C} = 360^{0} : 3 = 120^{\circ}$ .

$\Rightarrow s đ \overset{⏜}{A C} = s đ \overset{⏜}{B C} - s đ \overset{⏜}{A B}$ $= 120^{\circ} - 90^{\circ} = 30^{\circ}$

$\Rightarrow \hat{A B C} = \frac{1}{2} s đ \overset{⏜}{A C} = 15^{\circ}$ (tính chất góc nội tiếp)

Trong $∆ A H B$ có $\hat{A H B} = 90^{\circ}$

$\Rightarrow A H = A B . \sin \hat{A B H}$ $= R \sqrt{2} . \sin 15^{\circ} \approx 0, 36 R$

Trong $∆ A H C$ có $\hat{A H C} = 90^{\circ}$

$\hat{A C B} = \frac{1}{2}$ sđ $\overset{⏜}{A B} = 45^{\circ}$ (tính chất góc nội tiếp)

$A C = \frac{A H}{\sin \hat{A C H}}$ $= \frac{A H}{\sin 45^{\circ}} \approx \frac{0, 36 R}{\sin 45^{\circ}} \approx 0, 51 R$

Bài 51 trang 108 SBT Toán 9 tập 2: Cho ngũ giác đều $A B C D E .$ Gọi $I$ là giao điểm của $A D$ và $B E .$ Chứng minh $D I^{2} = A I . A D$
Phương pháp giải:

Ta sử dụng kiến thức:

+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.

+) Số đo góc ở tâm chắn mỗi cạnh của đa giác đều $n$ cạnh bằng $\frac{360^{\circ}}{n} .$

+) Nếu $C$ là một điểm trên cung $A B$ thì: $s đ \overset{⏜}{A B} = s đ \overset{⏜}{A C} + s đ \overset{⏜}{C B} .$

+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.

Lời giải:

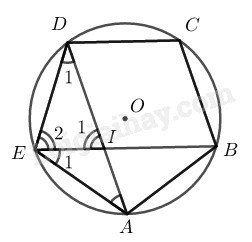
SBT Toán 9 Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp | Giải SBT Toán lớp 9 (ảnh 8)

Vẽ đường tròn ngoại tiếp ngũ giác đều $A B C D E$

$s đ \overset{⏜}{A B} = s đ \overset{⏜}{B C} = s đ \overset{⏜}{C D}$ $= s đ \overset{⏜}{D E} = s đ \overset{⏜}{A E} = \frac{360^{\circ}}{5} = 72^{\circ}$ $(1)$

$\hat{E_{1}} = \frac{1}{2} s đ \overset{⏜}{A B}$ (tính chất góc nội tiếp) $(2)$

$\hat{D_{1}} = \frac{1}{2} s đ \overset{⏜}{A E}$ (tính chất góc nội tiếp) $(3)$

Từ $(1),$ $(2)$ và $(3)$ suy ra: $\hat{E_{1}} = \hat{D_{1}}$

Xét $∆ A I E$ và $∆ A E D :$

+) $\hat{E_{1}} = \hat{D_{1}}$ (chứng minh trên)

+) $\hat{A}$ chung

Suy ra: $∆ A I E$ đồng dạng $∆ A E D (g . g)$

Do đó: $\frac{A I}{A E} = \frac{A E}{A D}$

$\Rightarrow$ $A E^{2} = A I . A D$ $(*)$

Lại có: $\hat{E_{2}} = \frac{1}{2} s đ \overset{⏜}{B C D}$ (tính chất góc nội tiếp) hay $\hat{E_{2}} = \frac{1}{2} (s đ \overset{⏜}{B C} + s đ \overset{⏜}{C D}$ ) $(4)$

$\hat{I_{1}} = \frac{1}{2} (s đ \overset{⏜}{D E} + s đ \overset{⏜}{A B}$ ) (tính chất góc có đỉnh ở trong đường tròn) $(5)$

Từ $(1),$ $(4)$ và $(5)$ suy ra: $\hat{E_{2}} = \hat{I_{1}}$

$\Rightarrow$ $∆ D E I$ cân tại $D$ $\Rightarrow D E = D I$

$D E = A E (g t)$

Suy ra: $D I = A E (* *)$

Từ $(*)$ và $(* *)$ suy ra: $D I^{2} = A I . A D$

Bài tập bổ sung (trang 109 SBT Toán 9)

Bài 8.1 trang 109 SBT Toán 9 tập 2: Mỗi câu sau đây đúng hay sai?

$a)$ Mỗi tam giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp.

$b)$ Mỗi tứ giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp.

$c)$ Giao điểm ba đường trung tuyến của một tam giác là tâm đường tròn ngoại tiếp tam giác ấy.

$d)$ Giao điểm ba đường trung trực của một tam giác là tâm đường tròn ngoại tiếp tam giác ấy.

$e)$ Giao điểm ba đường phân giác trong của một tam giác là tâm đường tròn nội tiếp tam giác ấy.

$f)$ Giao điểm ba đường cao của một tam giác là tâm đường tròn nội tiếp tam giác ấy.

$g)$ Tứ giác có tổng độ dài các cặp cạnh đối nhau bằng nhau thì ngoại tiếp được đường tròn.

$h)$ Tứ giác có tổng số đo các cặp góc (trong) đối nhau bằng nhau thì nội tiếp được đường tròn.

$i)$ Đường tròn tiếp xúc với các đường thẳng chứa các cạnh của tam giác là đường tròn nội tiếp tam giác đó.

Phương pháp giải:

Ta sử dụng kiến thức:

+) Bất kì đa giác đều nào cũng có một và chỉ một đường tròn ngoại tiếp, có một và chỉ một đường tròn nội tiếp.

+) Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác.

+) Đường tròn tiếp xúc với tất cả các cạnh của đa giác được gọi là đường tròn nội tiếp đa giác.

Lời giải:

Câu $a :$ Đúng

Câu $b :$ Sai

Câu $c :$ Sai vì giao ba đường trung trực là tâm đường tròn ngoại tiếp tam giác.

Câu $d :$ Đúng

Câu $e :$ Đúng

Câu $f :$ Sai vì giao ba đường phân giác là tâm đường tròn nội tiếp tam giác.

Câu $g :$ Đúng

Câu $h :$ Đúng

Câu $i :$ Sai vì nó còn có thể là đường tròn bàng tiếp tam giác.

Bài 8.2 trang 109 SBT Toán 9 tập 2: Cho đường tròn tâm $O$ bán kính $R$ và điểm $M$ ở ngoài đường tròn đó. Qua điểm $M$ kẻ hai tiếp tuyến $M A,$ $M B$ với đường tròn $(O) .$ Qua điểm $M$ kẻ cát tuyến $M C D$ với đường tròn $(O)$ (tức là đường thẳng đi qua điểm $M$ và cắt đường tròn tại hai điểm $C, D) .$ Gọi $I$ là trung điểm của dây $C D .$ Khi đó $M A O I B$ có là ngũ giác nội tiếp hay không $?$
Phương pháp giải:

Ta sử dụng kiến thức:

+) Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.

+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

+) Nếu các đỉnh của đa giác cùng nhìn một cạnh dưới góc vuông thì đa giác đó nội tiếp đường tròn.

Lời giải:

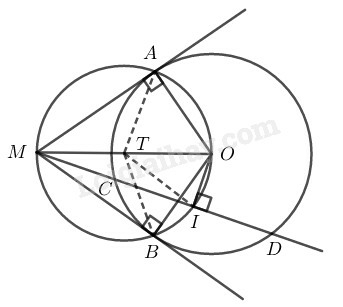
SBT Toán 9 Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp | Giải SBT Toán lớp 9 (ảnh 9)

Khi cát tuyến $M C D$ không đi qua $O .$

Xét đường tròn $(O)$ có:

$I C = I D (g t)$

$\Rightarrow$ $O I ⊥ C D$ (đường kính đi qua điểm chính giữa của dây không đi qua tâm thì vuông góc với dây đó)

$\Rightarrow \hat{M I O} = 90^{\circ}$

$M A ⊥ O A$ (tính chất tiếp tuyến)

$\Rightarrow \hat{M A O} = 90^{\circ}$

$M B ⊥ O B$ (tính chất tiếp tuyến)

$\Rightarrow \hat{M B O} = 90^{\circ}$

$A, I, B$ nhìn $M O$ dưới một góc bằng $90^{\circ}$ nên $A, I, B$ nằm trên đường tròn đường kính $M O .$

Vậy: Ngũ giác $M A O I B$ nội tiếp.

(Khi cát tuyến $M C D$ đi qua $O$ ngũ giác $M A O I B$ suy biến thành tứ giác $M A O B$ chứng minh tương tự).

Bài liên quan:

Leave a Comment Hủy