Bài tập Toán 9 Chương 4 Bài 1: Hình Trụ- Diện tích xung quanh và thể tích của hình trụ
A. Bài tập Hình trụ – Diện tích xung quanh và thể tích của hình trụ
I. Bài tập trắc nghiệm
Câu 1: Cho hình trụ có chu vi đáy là 8π và chiều cao h = 10. Tính thể tích hình trụ:
A. 80π
B. 40π
C. 160π
D. 150π
Lời giải:
Chọn đáp án C.
Câu 2: Cho hình trụ có bán kính đáy R = 4 (cm) và chiều cao h = 5 (cm). Diện tích xung quanh của hình trụ là:
A. 40π
B. 30π
C. 20π
D. 50π
Lời giải:
Diện tích xung quanh của hình trụ là:
Sxq = 2πRh = 2π.4.5 = 40π (cm2)
Chọn đáp án A.
Câu 3: Cho hình trụ có bán kính đáy R = 8cm và diện tích toàn phần 564π cm2. Tính chiều cao của hình trụ:
A. 27cm
B. 27,25cm
C. 25cm
D. 25,27cm
Lời giải:
Ta có diện tích toàn phần của hình trụ:
Chọn đáp án B.
Câu 4: Cho hình trụ có bán kính đáy R và chiều cao h. Nếu ta tăng chiều cao lên hai lần và giảm bán kính đáy đi hai lần thì:
A. Thể tích hình trụ không đổi
B. Diện tích toàn phần không đổi
C. Diện tích xung quanh không đổi
D. Chu vi đáy không đổi
Lời giải:
Chọn đáp án C.
Câu 5: Hộp sữa Ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao h = 12cm và đường kính đáy h = 8cm. Tính diện tích toàn phần của hộp sữa. Lấy π ≃ 3,14
A. 110π (cm2)
B. 128π (cm2)
C. 96π (cm2)
D. 112π (cm2)
Lời giải:
Diện tích toàn phần của hộp sữa:
Chọn đáp án D.
Câu 6: Chiều cao của 1 hình trụ bằng bán kính đường tròn đáy. Diện tích xung quanh của hình trụ là 628cm2. Tính thể tích hình trụ.
A. 1000π
B. 100π
C. 500π
D.Đáp án khác
Lời giải:
Chọn đáp án A.
Câu 7: Một hình trụ có bán kính đáy R = 2cm và diện tích xunh quanh là Sxq = 100π . Tính diện tích toàn phần của hình trụ?
A. 140π
B. 104π
C. 120π
D. 108π
Lời giải:
Chọn đáp án B.
Câu 8: Tính diện tích xung quanh của một hình trụ có chu vi đường tròn đáy là 4π và chiều cao h =2.
A. 12π
B. 4π
C. 8π
D. 16π
Lời giải:
Chọn đáp án C.
Câu 9: Cho một hình trụ có diện tích xung quanh bằng diện tích hai đáy. Khi đó:
A. r = 2h
B. h = 2r
C. h = 4r
D. r = h
Lời giải:
Vì diện tích xung quanh bằng diện tích hai đáy nên:
Chọn đáp án D.
Câu 10: Nếu tăng bán kính đáy của hình trụ lên 4 lần và giữ nguyên chiều cao thì thể tích mới của hình trụ”
A. Gấp 4 lần
B. Gấp 8 lần
C. Gấp 12 lần
D. Gấp 16 lần
Lời giải:
Chọn đáp án D.
Câu 11: Cho hình trụ có bán kính đáy R = 12 cm và diện tích toàn phần 672π cm2. Tính chiều cao của hình trụ
A. 16cm
B. 18cm
C. 8cm
D. 20cm
Lời giải:
Đáp án cần chọn là: A
Câu 12: Cho hình trụ có bán kính đáy R và chiều cao h. Nếu ta tăng chiều cao lên hai lần và giảm bán kính đáy đi hai lần thì
A. Thể tích hình trụ không đổi
B. Diện tích toàn phần không đổi
C. Diện tích xung quanh không đổi
D. Chu vi đáy không đổi
Lời giải:
Chiều cao mới của hình trụ là h’ = 2h; bán kính mới là
Hình trụ mới có:
Chu vi đáy = C nên Phương án D sai
Diện tích toàn phần nên Phương án B sai
Thể tích nên Phương án A sai
Diện tích xung quanh nên Phương án C đúng
Đáp án cần chọn là: C
Câu 13: Chọn câu đúng. Cho hình trụ có bán kính đáy R và chiều cao h. Nếu ta giảm chiều cao đi chín lần và tăng bán kính đáy lên ba lần thì
A. Thể tích hình trụ không đổi
B. Diện tích toàn phần không đổi
C. Diện tích xung quanh không đổi
D. Chu vi đáy không đổi
Lời giải:
Chiều cao mới của hình trụ là ; bán kính đáy mới là R’ = 3R
Hình trụ mới có:
Chu vi đáy 2πR’ = 2π.3R = 6πR = 3.2πR = 3C nên phương án D sai
Thể tích nên phương án A đúng
Diện tích xung quanh nên phương án C sai
Đáp án cần chọn là: A
Câu 14: Hộp sữa ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao h = 12cm và đường kính đáy là d = 8cm. Tính diện tích toàn phần của hộp sữa. Lấy π ≈ 3,14
A. 110π (cm2)
B. 128π (cm2)
C. 96π (cm2)
D. 112π (cm2)
Lời giải:
Bán kính đường tròn đáy R = = 4cm nên diện tích một đát Sd = πR2 = 16π (cm2)
Ta có diện tích xung quanh của hình trụ Sxq = 2πRh = 2π.4.12 = 96 (cm2)
Vì hộp sữa đã mất nắp nên diện tích toàn phần của hộp sữa
Stp = 96π + 16π = 112π (cm2)
Đáp án cần chọn là: D
Câu 15: Hộp sữa ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao h = 10cm và đường kính đáy là d = 6cm. Tính diện tích toàn phần của hộp sữa. Lấy π ≈ 3,14
A. 110π (cm2)
B. 129π (cm2)
C. 96π (cm2)
D. 69π (cm2)
Lời giải:
Bán kính đường tròn đáy R = = 3cm nên diện tích một đát Sd = πR2 = 9 (cm2)
Ta có diện tích xung quanh của hình trụ Sxq = 2πRh = 2π.3.10 = 60 (cm2)
Vì hộp sữa đã mất nắp nên diện tích toàn phần của hộp sữa
Stp = 9π + 60π = 69π (cm2)
Đáp án cần chọn là: D
II. Bài tập tự luận có lời giải
Câu 1: Một hình trụ có bán kính đáy bằng 1/4 đường cao. Khi cắt hình trụ này bằng một mặt phẳng đi qua trục thì mặt cắt là một hình chữ nhật có diện tích là 50cm2. Tính diện tích xung quanh và thể tích hình trụ.
Lời giải:
Theo giả thiết ta có
III. Bài tập vận dụng
Câu 1: Tính diện tích xung quanh và diện tích toàn phần của hình sau
Câu 2: Hình chữ nhật ABCD có AB = a, BC = 3a . Quay hình chữ nhật quanh cạnh AB thì được thể tích V1, quay quanh cạnh BC thì được thể tích V2. Tỉ số thể tích giữa V1 và V2 là?
B. Lý thuyết Hình trụ – Diện tích xung quanh và thể tích của hình trụ
1. Hình trụ
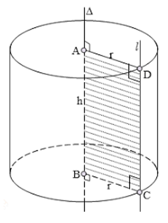
Khi quay hình chữ nhật ABCD một vòng quanh cạnh AB cố định, ta được một hình trụ.
– Hai hình tròn (A) và (B) bằng nhau và nằm trong hai mặt phẳng song song được gọi là hai đáy của hình trụ.
– Đường thẳng AB được gọi là trục của hình trụ.
– Mỗi vị trí của CD được gọi là một đường sinh. Các đường sinh vuông góc với hai mặt phẳng đáy. Độ dài của đường sinh là chiều cao của hình trụ.
Ví dụ 1. Một số vật có dạng hình trụ trong thực tế như: hộp sữa bột, cốc thủy tinh đựng nước, lon nước ngọt,…
Hình minh họa:
2. Cắt hình trụ bởi một mặt phẳng
– Khi cắt hình trụ bởi một mặt phẳng song song với đáy, thì phần mặt phẳng nằm trong hình trụ (mặt cắt – thiết diện) là một hình tròn bằng hình tròn đáy.
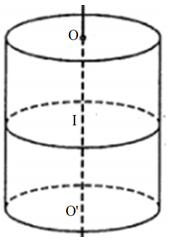
Ví dụ 2. Hình trụ bị cắt bởi mặt phẳng song song với hai đáy thì phần mặt phẳng nằm trong hình trụ (mặt cắt) là hình tròn (I) bằng hình tròn đáy (hình tròn (O) và (O’)) (như hình vẽ).
– Khi cắt hình trụ bởi một mặt phẳng song song với trục OO’ thì mặt cắt là một hình chữ nhật.
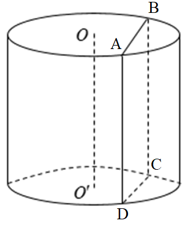
Ví dụ 3. Hình trụ bị cắt bởi mặt phẳng ABCD, mặt phẳng này song song với OO’ thì mặt cắt là hình chữ nhật ABCD (như hình vẽ).
3. Diện tích và thể tích hình trụ
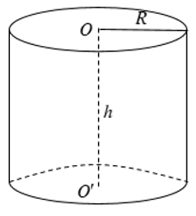
Cho hình trụ có bán kính đáy R và chiều cao h.
– Diện tích xung quanh: Sxq = 2πRh.
– Diện tích toàn phần: Stp = 2πRh + 2πR2.
– Thể tích: V = πR2h.
Ví dụ 4. Cho hình trụ có bán kính đáy R = 3 cm và chiều cao h = 6 cm. Tính diện tích xung quanh của hình trụ.
Lời giải:
Diện tích xung quanh của hình trụ là:
Sxq = 2πRh = 2π . 3 . 6 = 36 π (cm2).
Xem thêm