Giải SBT Toán 9 Phần hình học: Ôn tập cuối năm
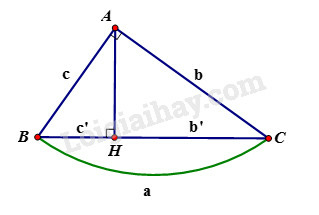
Bài 1 trang 195 SBT Toán 9 tập 2: (Xem hình 122). Tính:
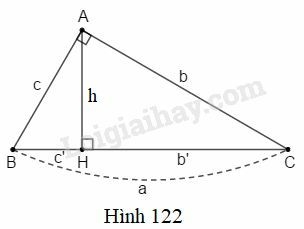
a) và biết
b) và , biết
c) và biết
d) biết
Phương pháp giải:
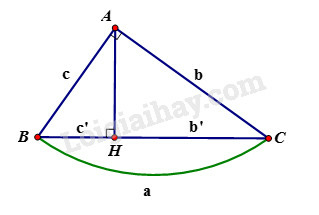
Cho tam giác vuông tại , đường cao . Khi đó ta có các hệ thức sau:
+) hay
+) hay
+) hay
+) hay
+) hay (định lý Pytago)
Lời giải:
a)
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông vào tam giác vuông tại , ta có:
b) Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông vào tam giác vuông tại , ta có:
c) Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông vào tam giác vuông tại , ta có:
d) Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông vào tam giác vuông tại , ta có:
Bài 2 trang 195 SBT Toán 9 tập 2: (Xem hình 122). Chứng minh rằng:
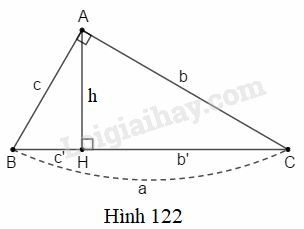
Phương pháp giải:
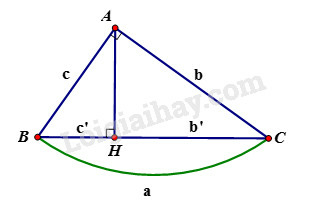
– Cho tam giác vuông tại , đường cao . Khi đó ta có các hệ thức sau:
+) hay
+) hay
– Diện tích tam giác bằng tích của chiều cao hạ từ đỉnh đến cạnh đối diện với độ dài cạnh đối diện của đỉnh đó.
Lời giải:
a) Diện tích tam giác là:
b) Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông vào tam giác vuông tại , ta có:
Từ (1) và (2) suy ra: .
Bài 3 trang 195 SBT Toán 9 tập 2: Cho tam giác có và Kẻ đường cao . Tính độ dài các đoạn thẳng và
Phương pháp giải:
Sử dụng:
– Định lí Pytago đảo: Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.
– Cho tam giác vuông tại , đường cao . Khi đó ta có các hệ thức sau:
+) hay .
+) hay .
Lời giải:
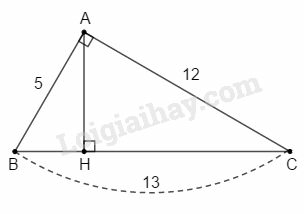
Ta có:
Theo định lí Pytago đảo thì tam giác vuông tại .
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông vào tam giác vuông tại , ta có:
Bài 4 trang 196 SBT Toán 9 tập 2: Tính sin, cos, tang của các góc và của tam giác vuông ở biết:
a)
b)
c)
d)
Phương pháp giải:
Sử dụng:
– Định lí Pytago: Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
– Trong tam giác vuông các tỉ số lượng giác của góc nhọn được định nghĩa như sau:
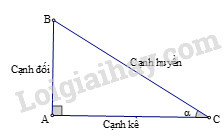
Lời giải:
a) Áp dụng định lí Pytago vào tam giác vuông tại , ta có:
Tam giác vuông tại nên và là hai góc phụ nhau, ta có:
b) Áp dụng định lí Pytago vào tam giác vuông tại , ta có:
.
Tam giác vuông tại nên và là hai góc phụ nhau, ta có:
c) Áp dụng định lí Pytago vào tam giác vuông tại , ta có:
Tam giác vuông tại nên và là hai góc phụ nhau, ta có:
d) Áp dụng định lí Pytago vào tam giác vuông tại , ta có:
Tam giác vuông tại nên và là hai góc phụ nhau, ta có:
Bài 5 trang 196 SBT Toán 9 tập 2: là đường phân giác của tam giác Chứng minh rằng
Phương pháp giải:
Sử dụng:
– Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
– Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
Lời giải:
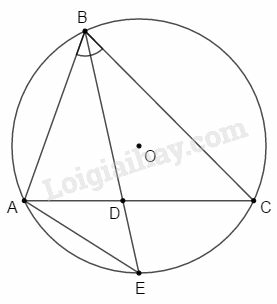
Gọi là giao điểm của tia và đường tròn ngoại tiếp .
* Xét và có:
(vì là tia phân giác )
(hai góc nội tiếp cùng chắn cung )
(g.g)
Mà nên
(1)
* Xét và có:
(hai góc đối đỉnh)
(hai góc nội tiếp cùng chắn cung )
(g.g)
(2)
Từ (1) và (2) suy ra: (điều phải chứng minh).
Bài 6 trang 196 SBT Toán 9 tập 2: Cho đường tròn . Khoảng cách từ đến dây của đường tròn bằng , . Trên dây lấy một điểm sao cho (h.123). Độ dài đoạn là:
(A) (B)
(C) (D)
Hãy chọn đáp số đúng.
Phương pháp giải:
Sử dụng: Trong tam giác cân đường cao ứng với cạnh đáy đồng thời là đường trung tuyến, đường trung trực, đường phân giác.
Lời giải:
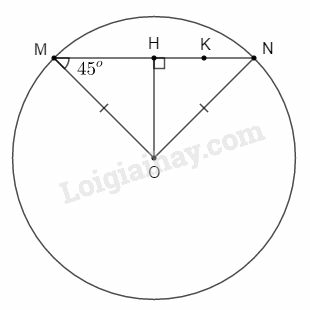
Gọi là chân đường cao hạ từ đến .
có nên vuông cân tại .
.
Lại có có bán kính nên cân tại .
Do đó vừa là đường cao đồng thời là trung tuyến của .
Ta có: .
Mà nên
Chọn A.
Bài 7 trang 196 SBT Toán 9 tập 2: Cho đường tròn và một điểm sao cho Kẻ tiếp tuyến với đường tròn là tiếp điểm (h.124). Số đo của góc là:
(A) (B)
(C) (D)
Hãy chọn đáp số đúng.
Phương pháp giải:
Sử dụng:
– Trong tam giác vuông các tỉ số lượng giác của góc nhọn được định nghĩa như sau:
Lời giải:
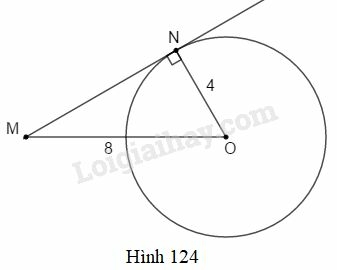
Xét vuông tại ta có:
Chọn D.
Bài 8 trang 196 SBT Toán 9 tập 2: Cho đường tròn và đường tròn có đoạn nối tâm . Đường tròn cắt tại , đường tròn cắt tại (h.125). Độ dài bằng:
(A) (B)
(C) (D)
Hãy chọn đáp số đúng.
Phương pháp giải:
Ta có: từ đó ta tính được .
Lời giải:
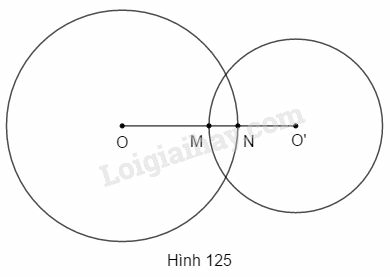
Ta có:
Chọn D.
Bài 9 trang 196 SBT Toán 9 tập 2: Trên hình 126, số đo góc nhỏ hơn số đo góc là . Tổng số đo hai góc và là:
(A) (B)
(C) (D)
Hãy chọn đáp số đúng.
Phương pháp giải:
Sử dụng: Góc nội tiếp (nhỏ hơn hoặc bằng ) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
Lời giải:
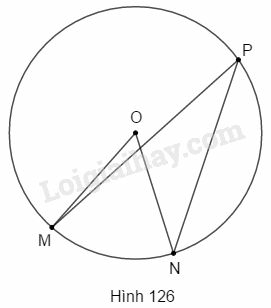
Xét đường tròn có:
(góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung).
Mặt khác:
(gt)
.
.
Vậy .
Chọn B.
Bài 10 trang 197 SBT Toán 9 tập 2: Cho hai đường tròn và tiếp xúc ngoài tại . Gọi là tiếp tuyến chung ngoài của hai đường tròn . Kẻ tiếp tuyến chung tại cắt ở .
a) Tính góc .
b) Tính độ dài .
c) Gọi là trung điểm của . Chứng minh rằng là tiếp tuyến của đường tròn tâm , bán kính .
Phương pháp giải:
Sử dụng:
* Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:
– Điểm đó cách đều hai tiếp điểm.
– Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
– Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm
* Trong tam giác vuông đường trung tuyến ứng với cạnh bằng nửa cạnh huyền.
* Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.
Lời giải:
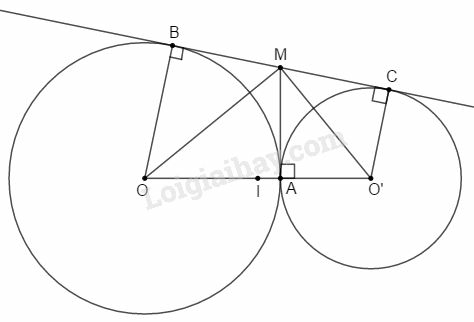
a) là tia phân giác của (tính chất hai tiếp tuyến cắt nhau).
là tia phân giác của (tính chất hai tiếp tuyến cắt nhau).
Ta có:
b) Xét vuông tại ta có:
Lại có (tính chất hai tiếp tuyến cắt nhau).
c)
Do đó tứ giác là hình thang.
Có nên là đường trung bình của hình thang . Do đó .
Mà nên .
vuông tại có là trung tuyến ứng với cạnh huyền nên .
Do đó là bán kính của đường tròn tâm lại vuông góc với tại nên là tiếp tuyến của .
Bài 11 trang 197 SBT Toán 9 tập 2: Cho tứ giác nội tiếp đường tròn có hai đường chéo và vuông góc với nhau. Chứng minh rằng .
Phương pháp giải:
Sử dụng:
– Trên một đường tròn hai dây song song chắn hai cung bằng nhau.
– Hai cung bằng nhau căng hai dây bằng nhau.
– Định lí Pytago: Trong tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của các cạnh góc vuông.
Lời giải:
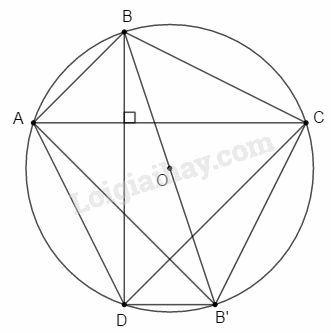
Kẻ đường kính . Nối .
(góc nội tiếp chắn nửa đường tròn).
Mặt khác (gt)
Vì nên
Mà
.
(các dây cung chắn các cung bằng nhau thì bằng nhau) (1)
Ta có (góc nội tiếp chắn nửa đường tròn).
Áp dụng định lí Pytago vào tam giác vuông có:
(2)
Từ (1) và (2) suy ra:
Hay .
Bài 12 trang 197 SBT Toán 9 tập 2: Cho tứ giác nội tiếp đường tròn . Trên đường chéo lấy điểm sao cho . Chứng minh:
a)
b)
Phương pháp giải:
Sử dụng:
– Các góc nội tiếp chắn cùng một cung hoặc chắn các cung bằng nhau thì bằng nhau.
– Hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
Lời giải:
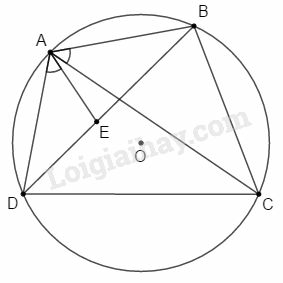
a) Xét và có:
(hai góc nội tiếp cùng chắn cung nhỏ )
(gt)
(g.g)
Ta có:
Mà (gt) nên
Xét và có:
(chứng minh trên)
(hai góc nội tiếp cùng chắn cung nhỏ )
(g.g).
b) Vì (câu a) suy ra
(1)
Vì (câu a) suy ra
(2)
Từ (1) và (2) ta có:
Vậy
Bài 13 trang 197 SBT Toán 9 tập 2: Cho nửa đường tròn đường kính và một dây . Qua vẽ đường thẳng vuông góc với , cắt tại . Các tiếp tuyến tại và của nửa đường tròn cắt đường thẳng theo thứ tự tại và . Chứng minh rằng:
a) Các tứ giác và nội tiếp được;
b) Tam giác vuông.
Phương pháp giải:
Sử dụng:
– Nếu tứ giác có tổng số đo hai góc đối diện bằng thì tứ giác đó nội tiếp được đường tròn.
– Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
– Hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
Lời giải:
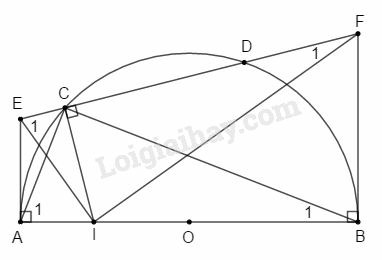
a)
Tứ giác có do đó tứ giác nội tiếp được.
Tứ giác có do đó tứ giác nội tiếp được.
b) Xét và có:
(hai góc nội tiếp cùng chắn cung của đường tròn ngoại tiếp tứ giác )
(hai góc nội tiếp cùng chắn cung của đường tròn ngoại tiếp tứ giác )
(g.g).
(hai góc tương ứng).
Ta lại có (góc nội tiếp chắn nửa đường tròn).
.
Vậy tam giác vuông tại .
Bài 14 trang 197 SBT Toán 9 tập 2: Cho tứ giác nội tiếp nửa đường tròn đường kính Hai đường chéo và cắt nhau tại Kẻ vuông góc với Gọi là trung điểm của . Chứng minh rằng:
a) Các tứ giác nội tiếp được;
b) Tia là tia phân giác của góc ;
c) Tứ giác nội tiếp được.
Phương pháp giải:
Sử dụng:
– Nếu tứ giác có tổng số đo hai góc đối diện bằng thì tứ giác đó nội tiếp được đường tròn.
– Trên một đường tròn các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
– Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới cùng một góc thì nội tiếp được.
Lời giải:
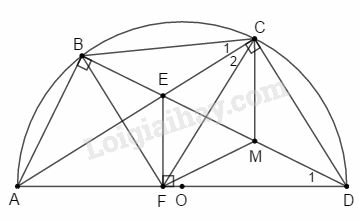
a) Ta có (góc nội tiếp chắn nửa đường tròn).
Tứ giác có nên tứ giác nội tiếp được.
Tứ giác có nên tứ giác nội tiếp được.
b) (hai góc nội tiếp cùng chắn cung nhỏ ) (1)
(hai góc nội tiếp cùng chắn cung của đường tròn ngoại tiếp tứ giác ) (2)
Từ (1) và (2) ta có .
Vậy là tia phân giác của góc .
c) vuông tại có là đường trung tuyến ứng với cạnh huyền nên .
cân tại .
(tính chất tam giác cân).
là góc ngoài tại đỉnh của nên:
(3)
Theo câu b) ta có: (4)
Từ (3) và (4) suy ra .
Vậy và cùng nhìn dưới một góc bằng nhau nên tứ giác nội tiếp được.
Bài 15 trang 197 SBT Toán 9 tập 2: Từ một điểm ở bên ngoài đường tròn ta vẽ hai tiếp tuyến với đường tròn. Trên cung nhỏ lấy một điểm Vẽ lần lượt vuông góc với . Gọi là giao điểm của và , là giao điểm của và . Chứng minh rằng:
a) Các tứ giác nội tiếp được;
b)
c) Tứ giác nội tiếp được;
d) .
Phương pháp giải:
Sử dụng:
– Nếu tứ giác có tổng số đo hai góc đối diện bằng thì tứ giác đó nội tiếp được đường tròn.
– Trên một đường tròn các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
Lời giải:
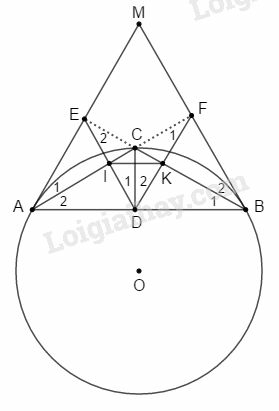
a) Ta có nên tứ giác nội tiếp được.
Ta có nên tứ giác nội tiếp được.
b) Có (hai góc nội tiếp cùng chắn cung của đường tròn ngoại tiếp tứ giác ) (1)
(góc giữa tia tiếp tuyến với một dây cung và góc nội tiếp cùng chắn cung của đường tròn tâm ) (2)
(hai góc nội tiếp cùng chắn cung của đường tròn ngoại tiếp tứ giác ) (3)
Từ (1), (2) và (3) suy ra: .
Có (hai góc nội tiếp cùng chắn cung của đường tròn ngoại tiếp tứ giác ) (4)
(góc giữa tia tiếp tuyến với một dây cung và góc nội tiếp cùng chắn cung của đường tròn tâm ) (5)
(hai góc nội tiếp cùng chắn cung của đường tròn ngoại tiếp tứ giác ) (6)
Từ (4), (5) và (6) suy ra: .
Xét và có:
(chứng minh trên)
(chứng minh trên)
(g.g).
c) Tứ giác có:
Suy ra tứ giác nội tiếp được.
d) Ta có (hai góc nội tiếp cùng chắn cung của đường tròn ngoại tiếp tứ giác ).
, mà và ở vị trí đồng vị nên .
Mặt khác (gt) nên .
Bài 16 trang 197 SBT Toán 9 tập 2: Một hình trụ có đường cao bằng đường kính đáy. Biết rằng thể tích hình trụ là . Tính diện tích xung quanh của nó.
Phương pháp giải:
Sử dụng:
– Công thức tính diện tích xung quanh hình trụ: .
– Công thức tính thể tích hình trụ: .
( là bán kính đường tròn đáy, là chiều cao, là diện tích đáy).
Lời giải:
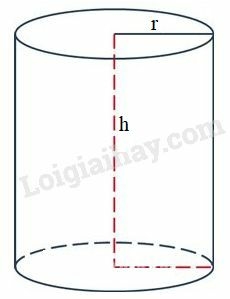
Hình trụ có đường cao bằng đường kính đáy nên .
Theo đề bài ta có:
Suy ra
Diện tích xung quanh của hình trụ là:
Bài 17 trang 198 SBT Toán 9 tập 2: Cho hình 127. Khi quay tam giác một vòng quanh cạnh cố định thì được:
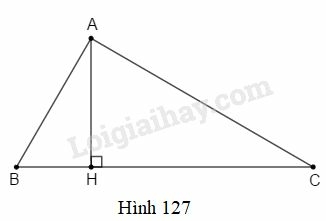
(A) một hình nón;
(B) hai hình nón;
(C) một hình trụ;
(D) một đường tròn.
Hãy chọn câu trả lời đúng.
Phương pháp giải:
Khi quay tam giác một vòng quanh cạnh cố định thì được hai hình nón có chung đáy và bán kính đáy là .
Lời giải:
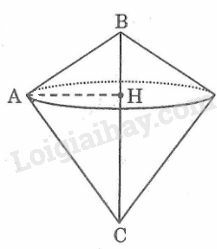
Khi quay tam giác một vòng quanh cạnh cố định thì được hai hình nón có chung đáy và bán kính đáy là .
Chọn B.
Bài 18 trang 198 SBT Toán 9 tập 2: Quay tam giác vuông một vòng quanh cạnh là được một hình nón. Tính thể tích và diện tích xung quanh của hình nón biết và
Phương pháp giải:
Áp dụng công thức:
– Diện tích xung quanh của hình nón: .
– Thể tích hình nón: .
( là bán kính đường tròn đáy, là đường sinh, là chiều cao).
Lời giải:
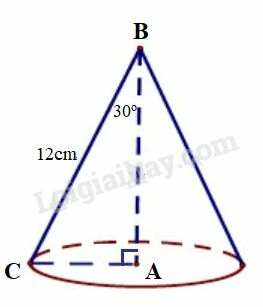
Xét vuông tại , ta có:
Quay tam giác vuông một vòng quanh cạnh ta được một hình nón có chiều cao bán kính đường tròn đáy là và đường sinh
Diện tích xung quanh của hình nón tạo thành là:
Thể tích của hình nón tạo thành là: