SBT Toán 9 Ôn tập chương 4: Hình trụ – Hình nón – Hình cầu | Giải SBT Toán lớp 9

Giải SBT Toán 9 Ôn tập chương 4: Hình trụ – Hình nón – Hình cầu

Bài 42 trang 174 SBT Toán 9 tập 2: Độ dài các cạnh của một tam giác $ABC$ vuông tại $A$, thỏa mãn các hệ thức sau:

$BC=AB+2a$  (1)

$AC=\frac{1}{2}\left(BC+AB\right)$ (2)

$a$ là một độ dài cho trước

a) Tính theo $a$, độ dài các cạnh và chiều cao $AH$ của tam giác.

b) Tam giác $ABC$ nội tiếp được trong nửa hình tròn tâm $O.$ Tính diện tích của phần thuộc nửa đường tròn nhưng ở ngoài tam giác đó.

c) Cho tam giác $ABC$ quay một vòng quanh cạnh huyền $BC.$ Tính tỉ số diện tích giữa các phần do các dây cung $AB$ và $AC$ tạo ra.

Phương pháp giải:

a) Đặt độ dài cạnh $AB=x$; điều kiện $x>0$. Suy ra $BC=x+2a$.

Theo định lí Pytago lập phương trình bậc hai ẩn $x$, từ đó giải phương trình tìm $x$.

b) Diện tích tam giác vuông có độ dài hai cạnh góc vuông lần lượt là $a;b$ là $S=\frac{1}{2}ab$.

Diện tích hình tròn bán kính $r$ là $S=\pi r^2.$

c) Diện tích xung quanh hình nón có bán kính đáy $r$, đường sinh $l$ là $S_{xq}=\pi rl$.

Lời giải:

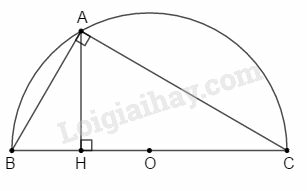
a) Đặt độ dài cạnh $AB=x$; điều kiện $x>0$.

Theo điều kiện (1) ta có: $BC=x+a$  (3)

Từ (2) và (3) $\Rightarrow AC=\frac{1}{2}\left(x+2a+x\right)=x+a$

Áp dụng định lí Pitago vào $\mathrm{\Delta }ABC$ vuông tại A, ta có:

$B{C}^2=A{B}^2+A{C}^2$

$\Rightarrow {\left(x+2a\right)}^2=x^2+{\left(x+a\right)}^2$

$\Rightarrow x^2+4ax+4a^2=x^2+x^2+2ax$$+a^2$

$\Rightarrow x^2-2ax-3a^2=0$

$\mathrm{\Delta }={\left(-2a\right)}^2-4.1\left(-3a^2\right)$$=4a^2+12a^2=16a^2>0$

$\Rightarrow \sqrt{\mathrm{\Delta }}=\sqrt{16a^2}=4a$

$x_1=\frac{2a+4a}{2.1}=\frac{6a}{2}=3a$

$x_2=\frac{2a-4a}{2.1}=-a$

Vì $x>0$ $\Rightarrow x_2=-a$  (loại)

Vậy cạnh $AB=3a;AC=3a+a=4a;$ $BC=3a+2a=5a$.

Ta có $AH.BC=AB.AC$ (hệ thức lượng trong tam giác vuông $ABC)$

$\Rightarrow AH=\frac{AB.AC}{BC}=\frac{3a.4a}{5a}$$=\frac{12a}{5}$

b) Diện tích của $\mathrm{\Delta }ABC$ là:

$S_1=\frac{1}{2}AB.AC=\frac{1}{2}.3a.4a=6a^2$ (đơn vị diện tích)

$\mathrm{\Delta }ABC$ nội tiếp trong đường tròn (O) có bán kính: $R=\frac{BC}{2}=\frac{5a}{2}$

Diện tích nửa hình tròn là: $S_2=\frac{1}{2}\pi .r^2=\frac{1}{2}\pi .{\left(\frac{5a}{2}\right)}^2$$=\frac{25\pi a^2}{8}$

Phần diện tích nửa hình tròn nằm ngoài tam giác là:

$S=S_2-S_1=\frac{25\pi a^2}{8}-6a^2$$=\frac{a^2}{8}\left(25\pi -48\right)$

 

c) Khi quay $\mathrm{\Delta }ABC$ một vòng quanh cạnh $BC$ thì $AB$ và $AC$ vạch lên hai hình nón có bán kính đáy là $AH.$

Diện tích xung quanh hình nón do dây cung $AB$ tạo ra là: 

$S_1=\pi .AH.AB=\pi .AH.3a$

Diện tích xung quanh hình nón do dây cung cung $AC$ tạo ra là:

$S_2=\pi .AH.AC=\pi AH.4a$

Tỉ số diện tích giữa các phần do các dây cung $AB$ và $AC$ tạo ra là:

$\frac{S_1}{S_2}=\frac{\pi .AH.3a}{\pi .AH.4a}=\frac{3}{4}$.

Bài 43 trang 174 SBT Toán 9 tập 2: Với một hình nón có bán kính đường tròn đáy là $r(cm)$ và chiều cao $2r(cm)$ và một hình cầu bán kính $r(cm).$ Hãy tính:

a) Diện tích mặt cầu, biết diện tích toàn phần của hình nón là $21,06\left(c{m}^2\right)$.

b) Thể tích hình nón, biết thể tích hình cầu là $15,8\left(c{m}^3\right)$.

Phương pháp giải:

Sử dụng:

– Diện tích xung quanh của hình nón: $S_{xq}=\pi rl$.

– Diện tích toàn phần của hình nón: $S_{tp}=\pi rl+\pi r^2$.

– Thể tích hình nón: $V=\frac{1}{3}\pi r^{2}h$.

($r$ là bán kính đường tròn đáy, $l$ là đường sinh, $h$ là chiều cao hình nón).

– Diện tích mặt cầu bán kính $r$ là: $S=4\pi r^2$.

– Thể tích hình cầu bán kính $r$ là: $V=\frac{4}{3}\pi r^3$.

Lời giải:

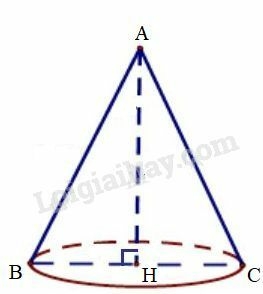
Hình nón đỉnh $A$ có bán kính đáy $HB=HC=r$ và chiều cao $AH=2r$

a) Áp dụng định lí Pytago vào tam giác vuông $AHB$, ta có:

$A{B}^2=A{H}^2+B{H}^2$$=4r^2+r^2=5r^2$

$\Rightarrow AB=r\sqrt{5}$ là đường sinh của hình nón.

Diện tích toàn phần hình nón:

$S_{TP}=S_{xq}+S_{\text{đáy}}$$=\pi .r.r\sqrt{5}+\pi r^2$$=\pi r^2\left(\sqrt{5}+1\right)$ 

$S_{TP}=21,06$

$\Rightarrow \pi r^2\left(\sqrt{5}+1\right)=21,06$

$\Rightarrow r^2=\frac{21,06}{\pi \left(\sqrt{5}+1\right)}$

Diện tích mặt cầu là:

$S=4\pi r^2$

$S=4\pi .\frac{21,06}{\pi \left(\sqrt{5}+1\right)}$$=21,06.\left(\sqrt{5}-1\right)\approx 26,03\left(c{m}^2\right)$

b) Thể tích hình cầu là: $V=\frac{4}{3}\pi r^3$

Thể tích hình cầu bằng $15,8c{m}^3$

$\Rightarrow \frac{4}{3}\pi r^3=15,8$

$\Rightarrow r^3=\frac{47,4}{4\pi }=\frac{23,7}{2\pi }$

Thể tích hình nón là: 

$V=\frac{1}{3}\pi r^2.h=\frac{1}{3}\pi r^2.2r=\frac{2}{3}\pi r^3$

$\Rightarrow V=\frac{2}{3}\pi .\frac{23,7}{2\pi }=\frac{23,7}{3}$$=7,9\left(c{m}^3\right)$.

Bài 44 trang 174 SBT Toán 9 tập 2: Một cái hộp hình trụ được làm ra sao cho một quả bóng hình cầu đặt vừa khít vào hộp đó (h.111).

Tỉ số $\frac{V_{\text{cầu}}}{V_{\text{trụ}}}$ là:

(A) $\frac{3}{4}$                                (C) $\frac{3}{2}$

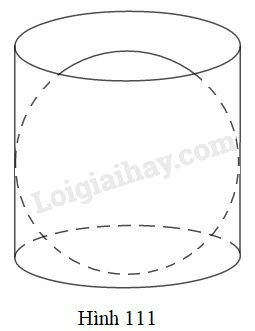
(B) $\frac{4}{3}$                                (D) $\frac{2}{3}$

Hãy chọn kết quả đúng.

Phương pháp giải:

Sử dụng:

– Thể tích hình cầu bán kính $r$ là: $V=\frac{4}{3}\pi r^3$.

– Công thức tính thể tích hình trụ là: $V=Sh=\pi r^{2}h$.

($r$ là bán kính đường tròn đáy, $h$ là chiều cao, $S$ là diện tích đáy).

Lời giải:

Hình cầu đặt khít trong hình trụ nên bán kính hình cầu bằng bán kính đáy hình trụ, chiều cao hình trụ bằng đường kính hình cầu.

Do đó, nếu gọi $r$ là bán kính đáy hình trụ thì $r$ cũng là bán kính hình cầu và chiều cao hình trụ là $2r$

Thể tích hình trụ là: $V_{\text{trụ}}=\pi .r^2.h=\pi r^2.2r=2\pi r^3$

Thể tích hình cầu là: $V_{\text{cầu}}=\frac{4}{3}\pi r^3$

$\Rightarrow \frac{V_{\text{cầu}}}{V_{\text{trụ}}}=\frac{2}{3}$

Chọn (D).

Bài 45 trang 174 SBT Toán 9 tập 2: Một hình trụ được “đặt khít” vào bên trong một hình cầu bán kính $r=12cm$ như hình 112. Hãy tính:

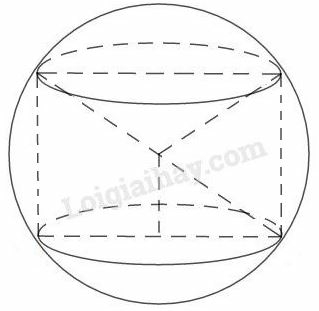
a) Diện tích xung quanh của hình trụ, biết chiều cao của hình trụ bằng đường kính đáy của nó.

b) Thể tích hình cầu.

c) Diện tích mặt cầu.

Phương pháp giải:

Sử dụng:

– Diện tích mặt cầu bán kính $r$ là: $S=4\pi r^2$.

– Thể tích hình cầu bán kính $r$ là: $V=\frac{4}{3}\pi r^3$.

– Công thức tính diện tích xung quanh hình trụ: $S_{xq}=2\pi rh$.

($r$ là bán kính đường tròn đáy, $h$ là chiều cao).

Lời giải:

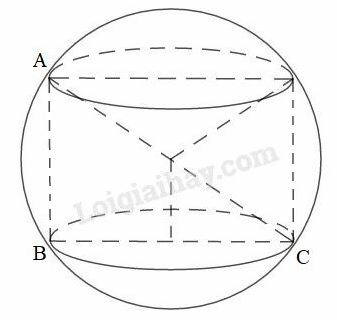
a) Đường chéo mặt cắt hình trụ đi qua trục là đường kính của hình cầu. Hình trụ có đường cao bằng đường kính đáy tức là $AB=BC$

Áp dụng định lí Pytago vào tam giác vuông $ABC$, ta có:

$\begin{array}{l}A{B}^2+B{C}^2=A{C}^2\\ \Rightarrow 2A{B}^2={\left(2.12\right)}^2={24}^2\\ \Rightarrow AB=12\sqrt{2}\left(cm\right).\end{array}$

Do đó bán kính đáy hình trụ là: $r=12\sqrt{2}:2=6\sqrt{2}\left(cm\right)$.

Diện tích xung quanh hình trụ là:

$S_{xq}=2\pi r.h$

$S_{xq}=2\pi .6\sqrt{2}.12\sqrt{2}=288\pi \left(c{m}^2\right)$

b) Thể tích hình cầu là:

$V=\frac{4}{3}\pi {.12}^3=2304\pi \left(c{m}^3\right)$

c) Diện tích mặt cầu là:

$S=4\pi {.12}^2=576\pi \left(c{m}^2\right)$.

Bài 46 trang 175 SBT Toán 9 tập 2: Cho bán kính của Trái Đất và Mặt Trăng tương ứng là $6371$ và $1738$ kilomet. Trong các số sau đây, số nào là tỉ số thể tích giữa Trái Đất và Mặt Trăng?

(A) $3,67$                             (C) $15,63$

(B) $4,93$                             (D) $49,26$.

Phương pháp giải:

Áp dụng công thức:

– Thể tích hình cầu bán kính $r$ là: $V=\frac{4}{3}\pi r^3$.

Lời giải:

Thể tích trái đất là: $V_1=\frac{4}{3}\pi {.6371}^3$

Thể tích của mặt trăng là: $V_2=\frac{4}{3}\pi {.1738}^3$

$\frac{V_1}{V_2}=\frac{{6371}^3}{{1738}^3}={\left(\frac{6371}{1738}\right)}^3\approx 49,26$

Chọn (D).

Bài 47 trang 175 SBT Toán 9 tập 2: Với nửa hình cầu bán kính $r$ và một hình trụ có bán kính đường tròn đáy và chiều cao đều bằng $h$.

a) Khi $r=12(cm)$ và thể tích hai hình bằng nhau thì giá trị $h(cm)$ làm tròn đến chữ số thập phân thứ nhất là bao nhiêu?

b) Khi $h=12(cm)$ và tổng diện tích nửa mặt cầu và diện tích “hình tròn đáy” gấp ba lần diện tích toàn phần của hình trụ thì $r(cm)$ bằng bao nhiêu?

Phương pháp giải:

Sử dụng:

– Diện tích mặt cầu bán kính $r$ là: $S=4\pi r^2$.

– Thể tích hình cầu bán kính $r$ là: $V=\frac{4}{3}\pi r^3$.

– Diện tích xung quanh hình trụ là: $S_{xq}=2\pi rh$

– Diện tích toàn phần hình trụ là: $S_{tp}=S_{xq}+2S_{đ}=2\pi rh+2\pi r^2$

– Tính thể tích hình trụ là: $V=Sh=\pi r^{2}h$.

($r$ là bán kính đường tròn đáy, $h$ là chiều cao hình trụ).

Lời giải:

a) Thể tích nửa hình cầu bán kính $12cm$ là:

$V=\frac{1}{2}.\frac{4}{3}\pi {.12}^3=1152\pi \left(c{m}^3\right)$

Bán kính đáy hình trụ là: $R=h$

Thể tích hình trụ là: $V=\pi R^2.h$$=\pi .h^2.h=\pi .h^3$

Theo đề bài ta có:

$V=\pi .h^3=1152\pi$

$\Rightarrow h^3=1152$

$\Rightarrow h=\sqrt[3]{1152}\approx 10,5\left(cm\right)$.

b) Khi $h=12(cm)$ thì bán kính đáy hình trụ là $R=12(cm)$.

Diện tích xung quanh hình trụ là:

$S_{xq}=2\pi R.h=2\pi .12.12=288\pi$ $\left(c{m}^2\right).$

Diện tích một mặt đáy của hình trụ là:

$S_{đ}=\pi R^2=\pi {.12}^2=144\pi \left(c{m}^2\right).$

Diện tích toàn phần của hình trụ là:

$S_{TP}=S_{xq}+2S_{đ}$$=288\pi +2.144\pi =576\pi \left(c{m}^2\right).$

Diện tích nửa mặt cầu là: $S_c=\frac{1}{2}.4\pi r^2=2\pi r^2\left(c{m}^2\right).$

Diện tích hình tròn đáy của nửa mặt cầu là: $S=\pi r^2\left(c{m}^2\right).$

Tổng diện tích nửa mặt cầu và diện tích “hình tròn đáy” gấp ba lần diện tích toàn phần của hình trụ nên ta có:

$\begin{array}{l}{S}_c+S=3S_{TP}\\ \Rightarrow 2\pi r^2+\pi r^2=3.576\pi \\ \Rightarrow 3\pi r^2=1728\pi \\ \Rightarrow r^2=576\\ \Rightarrow r=\sqrt{576}=24\left(cm\right).\end{array}$

Bài 48 trang 175 SBT Toán 9 tập 2: Hình bên (h.113) gồm một hình nón được đặt khít vào bên trong một cốc hình trụ, chúng có cùng đáy, cùng chiều cao. Người ta đổ vào đó một lượng nước lên đến một nửa chiều cao của hình. (Giả sử rằng nước không rò rỉ, không thẩm thấu vào bên trong hình nón)

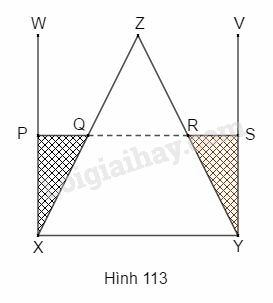
Hãy chọn đúng tỉ số giữa các đoạn thẳng $\frac{QR}{XY}$

(A) $\frac{1}{2}$;                             (B) $\frac{1}{3}$;

(C) $\frac{2}{3}$

(D) Không tính được, vì câu hỏi phụ thuộc vào bán kính đáy.

Phương pháp giải:

Sử dụng: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

Lời giải:

Vì hình trụ và hình nón có cùng chiều cao, người ta đổ nước lên đến nửa chiều cao của hình nên $Q$ là trung  điểm của $XZ$, $R$ là trung điểm của $YZ$. Do đó $RQ$ là đường trung bình của $\mathrm{\Delta }XYZ$.

Suy ra $\frac{QR}{XY}=\frac{1}{2}$ (tính chất đường trung bình của tam giác).

Chọn (A).

 

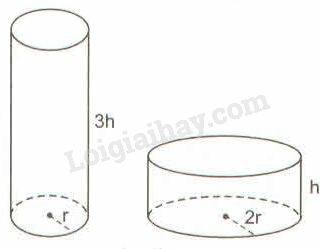
Bài 49 trang 175 SBT Toán 9 tập 2: Hai cái lọ có dạng hình trụ, các kích thước như ở hình 114. Lọ nào có dung tích lớn hơn?

Phương pháp giải:

Sử dụng:

– Công thức tính thể tích hình trụ: $V=Sh=\pi r^{2}h$.

($r$ là bán kính đường tròn đáy, $h$ là chiều cao, $S$ là diện tích đáy).

Lời giải:

Thể tích của hình trụ có bán kính đáy $r$ là:

$V_1=\pi r^2.3h=3\pi r^{2}h$ (đơn vị thể tích)

Thể tích của hình trụ có bán kính đáy $2r$ là:

$V_2=\pi {\left(2r\right)}^2.h=4\pi r^{2}h$ (đơn vị thể tích)

Dung tích hình trụ có bán kính đáy $r$ nhỏ hơn dung tích hình trụ có bán kính đáy $2r$.

Bài tập bổ sung (trang 176,177 SBT Toán 9)

Bài IV.1 trang 176 SBT Toán 9 tập 2: Một bể nước hình trụ có bán kính đáy là $0,8m$ và chiều cao là $1,2m.$ Người ta muốn làm một bể nước hình trụ mới có thể tích gấp $2$ lần bể nước cũ. Bạn An nói: Bể nước mới cần có bán kính dài gấp $2$ lần bán kính bể nước cũ. Bạn Ngọc nói: Bể nước mới cần có chiều cao gấp $2$ lần chiều cao của bể nước cũ.

Bạn Vân nói: Bể nước mới cần có cả chiều cao và bán kính đáy tương ứng gấp $2$ lần chiều cao và bán kính đáy của bể nước cũ.

Theo em, bạn nào nói đúng, tại sao?

Phương pháp giải:

Sử dụng:

– Công thức tính thể tích hình trụ: $V=Sh=\pi r^{2}h$.

($r$ là bán kính đường tròn đáy, $h$ là chiều cao, $S$ là diện tích đáy).

Lời giải:

Thể tích hình trụ có bán kính $r$ và đường cao $h$ là: $V=\pi r^2.h$

– Nếu tăng gấp đôi bán kính thì thể tích trụ là $V_1=\pi {\left(2r\right)}^{2}h=4\pi r^{2}h=4V$.

– Nếu tăng gấp đôi chiều cao thì thể tích hình trụ là: $V_2=\pi r^2.2h=2\pi r^{2}h=2V$.

– Nếu tăng gấp đôi bán kính và chiều cao thì thể tích hình trụ là:

$V_3=\pi {\left(2r\right)}^2.2h=8\pi r^{2}h=8V$.

Vậy bạn Ngọc nói đúng.

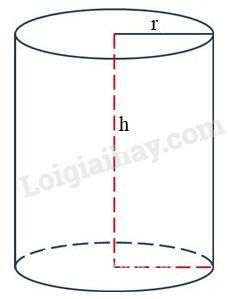
Bài IV.2 trang 176 SBT Toán 9 tập 2: Quan sát hình trụ ở hình bs.30 rồi điền số thích hợp vào ô trống trong bảng sau (lấy $\pi =3,14$)

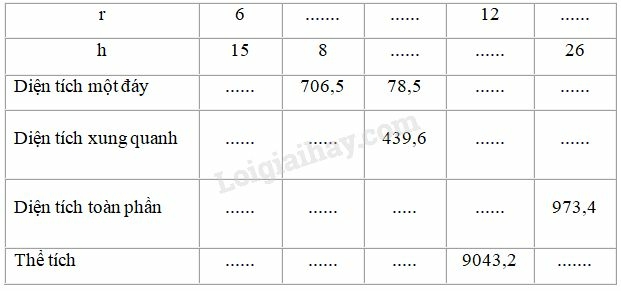
Phương pháp giải:

Sử dụng:

– Công thức tính diện tích xung quanh hình trụ: $S_{xq}=2\pi rh$.

– Công thức tính diện tích toàn phần hình trụ: $S_{tp}=S_{xq}+2S_{đ}=2\pi rh+2\pi r^2$.

– Công thức tính diện tích đáy hình trụ: $S_{đ}=\pi r^2$ .

– Công thức tính thể tích hình trụ: $V=Sh=\pi r^{2}h$.

($r$ là bán kính đường tròn đáy, $h$ là chiều cao).

Lời giải:

Ta điền vào bảng như sau:

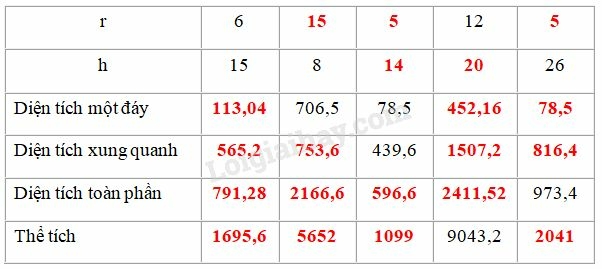
Giải thích:

* Hình trụ có $r=6;h=15$

Diện tích một đáy của hình trụ là: $S_{đ}=\pi r^2=\pi {.6}^2=113,04$

Diện tích xung quanh của hình trụ là: $S_{xq}=2\pi rh=2\pi .6.15=565,2$

Diện tích toàn phần của hình trụ là:

$S_{TP}=S_{xq}+2S_{đ}=565,2+2.113,04$$=791,28$

Thể tích của hình trụ là:

$V=\pi r^{2}h=\pi {.6}^2.15=1695,6$

* Hình trụ có $h=8;S_{đ}=706,5$

Ta có: $S_{đ}=\pi r^2$ $\Rightarrow r=\sqrt{\frac{S_{đ}}{\pi }}=\sqrt{\frac{706,5}{3,14}}=15$

$S_{xq}=2\pi rh=2\pi .15.8=753,6$

$S_{TP}=S_{xq}+2S_d=753,6+2.706,5$ $=2166,6$

$V=\pi r^{2}h=\pi {.15}^2.8=5652$

* Hình trụ có $S_{đ}=78,5;S_{xq}=439,6$

$S_{đ}=\pi r^2\Rightarrow r=\sqrt{\frac{S_{đ}}{\pi }}=\sqrt{\frac{78,5}{3,14}}=5$

$S_{xq}=2\pi rh\Rightarrow h=\frac{S_{xq}}{2\pi r}=\frac{439,6}{2.3,14.5}$$=14$

$S_{TP}=S_{xq}+2S_{đ}=439,6+2.78,5$$=596,6$

$V=\pi r^{2}h=\pi {.5}^2.14=1099$

* Hình trụ có $r=12;V=9043,2$

$V=\pi r^{2}h$ $\Rightarrow h=\frac{V}{\pi r^2}=\frac{9043,2}{3,{14.12}^2}=20$

$S_{đ}=\pi r^2=3,{14.12}^2=452,16$

$S_{xq}=2\pi rh=2.3,\mathrm{14.12.20}=1507,2$

$S_{TP}=S_{xq}+2S_d$$=1507,2+2.452,16$$=2411,52$

* Hình trụ có $h=26;S_{TP}=973,4$

$\begin{array}{l}{S}_{TP}=2\pi rh+2\pi r^2=973,4\\ \Rightarrow 2.3,14.r.26+2.3,14.r^2=973,4\\ \Rightarrow r^2+26r-155=0\\ \Rightarrow [\begin{array}{l}r=5\text{ (nhận)}\\ r=-31\text{ (loại)}\end{array}\end{array}$

$S_{đ}=\pi r^2=3,{14.5}^2=78,5$

$S_{xq}=2\pi rh=2.3,\mathrm{14.5.26}=816,4$

$V=\pi r^{2}h=3,{14.5}^2.26=2041$

Bài IV.3 trang 176 SBT Toán 9 tập 2: Thể tích của một hình nón thay đổi thế nào nếu:

a) Gấp đôi chiều cao của hình nón.

b) Gấp đôi bán kính của hình nón.

c) Gấp đôi cả chiều cao và bán kính đáy của hình nón.

Phương pháp giải:

Sử dụng:

– Công thức tính thể tích hình nón : $V=\frac{1}{3}\pi r^{2}h$.

($r$ là bán kính đường tròn đáy, $h$ là chiều cao).

Lời giải:

Hình nón  có bán kính đáy $r$, chiều cao $h$, có thể tích là: $V=\frac{1}{3}\pi r^{2}h$.

a) Nếu gấp đôi chiều cao thì thể tích hình nón là:

$V_1=\frac{1}{3}\pi r^2.\left(2h\right)=2.\frac{1}{3}\pi r^{2}h=2V$.

b) Nếu gấp đôi bán kính thì thể tích hình nón là:

$V_2=\frac{1}{3}\pi {\left(2r\right)}^2.h=4.\frac{1}{3}\pi r^{2}h=4V$.

c) Nếu gấp đôi cả bán kính và chiều cao thì hình nón có thể tích là:

$V_3=\frac{1}{3}\pi {\left(2r\right)}^2.2h=8.\frac{1}{3}\pi r^{2}h=8V$.

Bài IV.4 trang 177 SBT Toán 9 tập 2: Thể tích và diện tích của hình cầu thay đổi thế nào nếu bán kính hình cầu:

a) Tăng gấp $2$ lần?

b) Tăng gấp $3$ lần?

c) Giảm đi $2$ lần?

Phương pháp giải:

Sử dụng:

– Diện tích mặt cầu bán kính $r$ là: $S=4\pi r^2$.

– Thể tích hình cầu bán kính $r$ là: $V=\frac{4}{3}\pi r^3$.

Lời giải:

Hình cầu có bán kính $R$ có thể tích là: $V=\frac{4}{3}\pi R^3$ và diện tích $S=4\pi R^2$.

a) Nếu tăng bán kính gấp $2$ lần thì 

Thể tích hình cầu là: $V_1=\frac{4}{3}\pi {\left(2R\right)}^3=8.\frac{4}{3}\pi R^3=8V$

Diện tích hình cầu là: $S_1=4\pi {\left(2R\right)}^2=4.4\pi R^2=4S$

b) Nếu tăng bán kính gấp $3$ lần thì

Thể tích hình cầu là: $V_2=\frac{4}{3}\pi {\left(3R\right)}^3=27.\frac{4}{3}\pi R^3=27V$

Diện tích hình cầu là: $S_2=4\pi {\left(3R\right)}^2=9.4\pi R^2=9S$

c) Nếu giảm bán kính đi $2$ lần thì

Thể tích hình cầu là: $V_3=\frac{4}{3}\pi {\left(\frac{R}{2}\right)}^3=\frac{1}{8}.\frac{4}{3}\pi R^3=\frac{1}{8}V$

Diện tích hình cầu là: $S_3=4\pi {\left(\frac{R}{2}\right)}^2=\frac{1}{4}.4\pi R^2=\frac{1}{4}S$.

Bài IV.5 trang 177 SBT Toán 9 tập 2: Quan sát hình nón ở hình bs.31 rồi điền số thích hợp và các ô trống trong bảng sau (lấy $\pi =3,14)$)

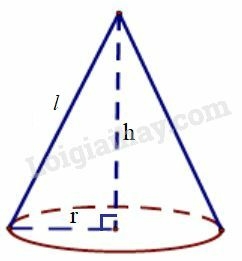
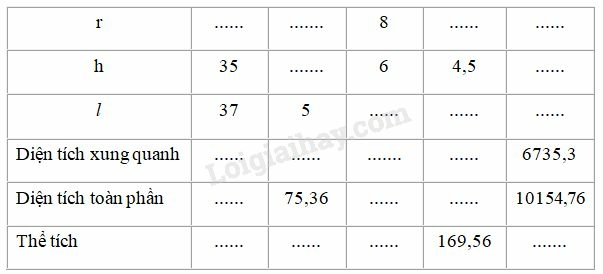
Phương pháp giải:

Sử dụng:

– Diện tích xung quanh của hình nón: $S_{xq}=\pi rl$.

– Diện tích toàn phần của hình nón: $S_{tp}=\pi rl+\pi r^2$.

– Thể tích hình nón: $V=\frac{1}{3}\pi r^{2}h$.

($r$ là bán kính đường tròn đáy, $l$ là đường sinh, $h$ là chiều cao).

Lời giải:

Ta điền được bảng sau:

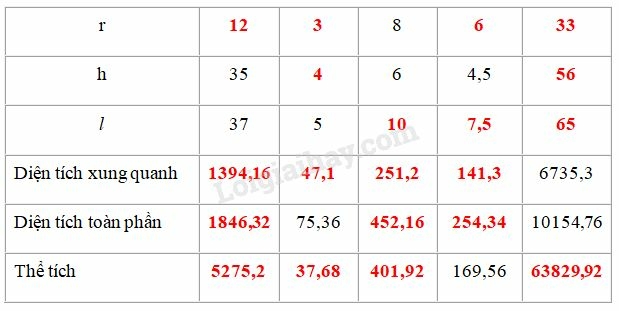
Giải thích: 

* Hình nón có $h=35;l=37$

Áp dụng định lí Pytago ta có:

$r=\sqrt{l^2-h^2}=\sqrt{{37}^2-{35}^2}=12$

$S_{xq}=\pi rl=3,\mathrm{14.12.37}=1394,16$

$S_{TP}=S_{xq}+\pi r^2$$=1394,16+3,{14.12}^2=1846,32$

$V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}.3,{14.12}^2.35$$=5275,2$

* Hình nón có $l=5;S_{TP}=75,36$

$\begin{array}{l}{S}_{TP}=\pi rl+\pi r^2=75,36\\ \Rightarrow 3,14.r.5+3,14.r^2=75,36\\ \Rightarrow r^2+5r-24=0\\ \Rightarrow [\begin{array}{l}r=3\text{ (nhận)}\\ r=-8\text{ (loại)}\end{array}\end{array}$

$h=\sqrt{l^2-r^2}=\sqrt{5^2-3^2}=4$

$S_{xq}=\pi rl=3,\mathrm{14.3.5}=47,1$

$V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}.3,{14.3}^2.4=37,68$

* Hình nón có $r=8;h=6$

$l=\sqrt{r^2+h^2}=\sqrt{8^2+6^2}=10$

$S_{xq}=\pi rl=3,\mathrm{14.8.10}=251,2$

$S_{TP}=\pi rl+\pi r^2=251,2+3,{14.8}^2$$=452,16$

$V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}.3,{14.8}^2.6=401,92$

* Hình nón có $h=4,5,V=169,56$

$V=\frac{1}{3}\pi r^{2}h$ $\Rightarrow r=\sqrt{\frac{3V}{\pi h}}=\sqrt{\frac{3.169,56}{3,14.4,5}}=6$

$l=\sqrt{r^2+h^2}=\sqrt{6^2+4,5^2}=7,5$

$S_{xq}=\pi rl=3,\mathrm{14.6.7},5=141,3$

$S_{TP}=\pi rl+\pi r^2=141,3+3,{14.6}^2$$=254,34$

* Hình nón có $S_{xq}=6735,3;S_{TP}=10154,76$

$\begin{array}{l}{S}_{xq}=\pi rl\\ S_{TP}=\pi rl+\pi r^2\\ S_{TP}-S_{xq}=\pi r^2\\ \Rightarrow \pi r^2=10154,76-6735,3\\ \Rightarrow \pi r^2=3419,46\\ \Rightarrow r=\sqrt{\frac{3419,46}{3,14}}=33\end{array}$

$S_{xq}=\pi rl$ $\Rightarrow l=\frac{S_{xq}}{\pi r}=\frac{6735,3}{3,14.33}=65$

$h=\sqrt{l^2-r^2}=\sqrt{{65}^2-{33}^2}=56$

$V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}.3,{14.33}^2.56$$=63829,92$

Bài IV.6 trang 177 SBT Toán 9 tập 2: Quan sát hình cầu ở hình bs.32 rồi điền số thích hợp vào các ô trống trong bảng sau (lấy $\pi =3,14)$)

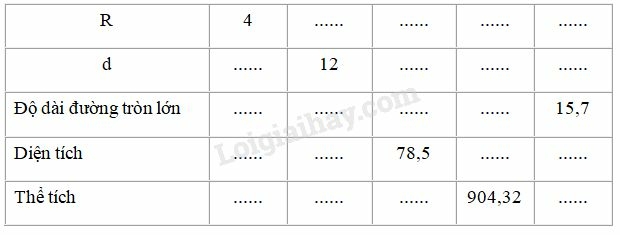
Phương pháp giải:

Sử dụng:

– Diện tích mặt cầu bán kính $r$ là: $S=4\pi r^2$.

– Thể tích hình cầu bán kính $r$ là: $V=\frac{4}{3}\pi r^3$.

Lời giải:

Ta điền được bảng sau:

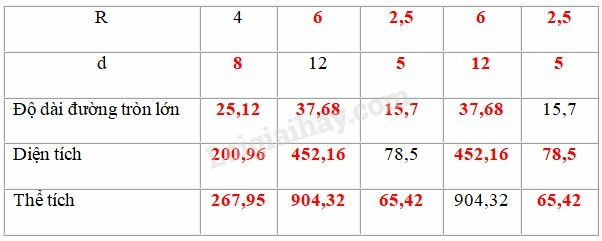
Giải thích: 

* Hình cầu có $R=4$

$d=2R=2.4=8$

Độ dài đường tròn lớn là:

$C=2\pi R=2.3,14.4=25,12$

$S=4\pi R^2=4.3,{14.4}^2=200,96$

$V=\frac{4}{3}\pi R^3=\frac{4}{3}.3,{14.4}^3\approx 267,95$

* Hình cầu có $d=12$

$\begin{array}{l}R=\frac{d}{2}=\frac{12}{2}=6\\ C=2\pi R=2.3,14.6=37,68\\ S=4\pi R^2=4.3,{14.6}^2=452,16\\ V=\frac{4}{3}\pi R^3=\frac{4}{3}.3,{14.6}^3=904,32\end{array}$

* Hình cầu có $S=78,5$

$S=4\pi R^2\Rightarrow R=\sqrt{\frac{S}{4\pi }}=\sqrt{\frac{78,5}{4.3,14}}$$=2,5$

$d=2R=2.2,5=5$

$C=2\pi R=2.3,14.2,5=15,7$

$V=\frac{4}{3}\pi R^3=\frac{4}{3}.3,14.2,5^3\approx 65,42$

* Hình cầu có $V=904,32$

$V=\frac{4}{3}\pi R^3\Rightarrow R=\sqrt[3]{\frac{3V}{4\pi }}$$=\sqrt[3]{\frac{3.904,32}{4.3,14}}=6$

$d=2R=2.6=12$

$C=2\pi R=2.3,14.6=37,68$

$S=4\pi R^2=4.3,{14.6}^2=452,16$

* Hình cầu có $C=15,7$

$C=2\pi R$ $\Rightarrow R=\frac{C}{2\pi }=\frac{15,7}{2.3,14}=2,5$

$d=2R=2.2,5=5$

$S=4\pi R^2=4.3,14.2,5^2=78,5$

$V=\frac{4}{3}\pi R^3=\frac{4}{3}.3,14.2,5^3\approx 65,42$