Giải SBT Toán 9 Bài 3: Góc nội tiếp
Bài 15 trang 102 SBT Toán 9 tập 2: Cho đường tròn tâm , bán kính . Hãy vẽ hình vuông có bốn đỉnh nằm trên đường tròn đó. Nêu cách vẽ.
Phương pháp giải:
+) Vẽ hình: dùng thước thẳng và compa để vẽ hình
+) Chứng minh: Sử dụng dấu hiệu nhận biết hình bình hành và hình vuông
Dấu hiệu nhận biết hình bình hành: Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Dấu hiệu nhận biết hình chữ nhật: Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
Dấu hiệu nhận biết hình vuông: Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
Lời giải:
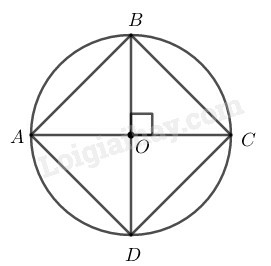
Cách vẽ:
– Vẽ đường tròn
– Vẽ 2 đường kính và vuông góc với nhau.
– Nối ta có tứ giác là hình vuông có đỉnh nằm trên cung tròn .
Chứng minh:
Theo cách vẽ ta có: nên tứ giác là hình bình hành
Lại có: nên hình bình hành là hình chữ nhật.
Mặt khác: nên hình chữ nhật là hình vuông.
Vậy tứ giác là hình vuông.
Bài 16 trang 102 SBT Toán 9 tập 2: Cho đường tròn và hai đường kính vuông góc với nhau. Lấy một điểm trên cung rồi vẽ tiếp tuyến với đường tròn tại Tiếp tuyến này cắt đường thẳng tại Chứng minh rằng
Phương pháp giải:
Ta sử dụng kiến thức:
+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung.
Lời giải:
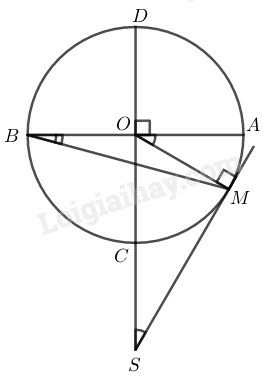
Xét đường tròn có (tính chất tiếp tuyến)
vuông tại
Nên
Lại có:
Suy ra: hay
Mà (góc ở tâm và góc nội tiếp cùng chắn cung )
Từ và suy ra:
Bài 17 trang 102 SBT Toán 9 tập 2: Cho đường tròn và hai dây bằng nhau. Qua vẽ một cát tuyến cắt dây ở và cắt đường tròn ở Chứng minh rằng
Phương pháp giải:
Ta sử dụng kiến thức:
+) Với hai cung nhỏ trong một đường tròn, hai dây bằng nhau căng hai cung bằng nhau.
+) Trong một đường tròn, góc nội tiếp chắn các cung bằng nhau thì bằng nhau.
Lời giải:
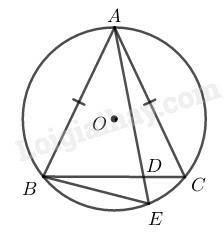
Vì
Nên (hai dây bằng nhau căng cung bằng nhau)
( góc nội tiếp chắn cung bằng nhau)
Xét và
+) chung
+) (chứng minh trên)
Suy ra: đồng dạng (g-g)
.
Bài 18 trang 102 SBT Toán 9 tập 2: Cho đường tròn và một điểm cố định không nằm trên đường tròn. Qua vẽ một cát tuyến bất kì cắt đường tròn ở và Chứng minh rằng tích không đổi.
Phương pháp giải:
sử dụng kiến thức:
+) Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau.
Lời giải:
* Trường hợp ở bên trong đường tròn
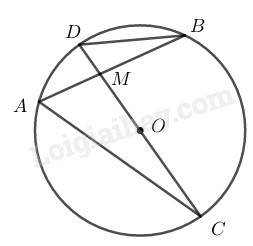
Kẻ cát tuyến bất kì của và đường thẳng cắt đường tròn tại và
Xét hai và
+) (đối đỉnh)
+) (hai góc nội tiếp cùng chắn cung )
Suy ra: đồng dạng
Vì cố định suy ra điểm và cố định nên độ dài của các đoạn và không đổi, suy ra tích không đổi
Từ và suy ra tích không đổi khi cát tuyến thay đổi.
* Trường hợp điểm ở ngoài đường tròn
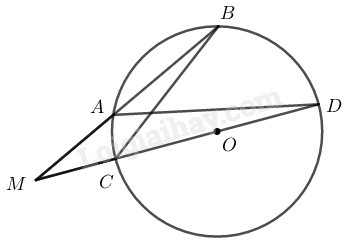
Kẻ cát tuyến bất kỳ của và đường thẳng cắt đường tròn tại và
Xét và
+) chung
+) (hai góc nội tiếp cùng chắn cung )
Suy ra: đồng dạng
Vì và cố định suy ra điểm cố định nên độ dài của các đoạn và không đổi, suy ra tích không đổi
Từ và suy ra tích không đổi khi cát tuyến thay đổi.
Bài 19 trang 102 SBT Toán 9 tập 2: Để giúp xe lửa chuyển từ một đường ray từ hướng này sang một đường ray theo hướng khác, người ta làm xen giữa một đoạn đường ray hình vòng cung (hình ). Biết chiều rộng của đường ray là , đoạn . Hãy tính bán kính của đoạn đường ray hình vòng cung.
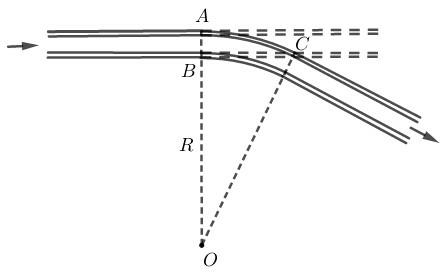
Phương pháp giải:
Ta sử dụng kiến thức:
+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
+) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+) Trong một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau.
Lời giải:
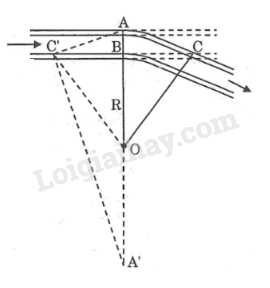
Ta xem hai đoạn đường ray thẳng là tiếp tuyến của hai đoạn đường ray vòng cung.
Điểm cố định nằm trong đường tròn có cung .
Đường thẳng cắt đường tròn đó tại và
cố định và cố định
là tiếp điểm cung nhỏ trong nên là tiếp tuyến của đường tròn
. Kéo dài cắt đường tròn tại
(đường kính vuông góc dây cung)
Xét và
+) (đối đỉnh)
+) ( góc nội tiếp cùng chắn cung )
Suy ra: đồng dạng
mà
Suy ra:
Bài 20 trang 102 SBT Toán 9 tập 2: Cho tam giác đều nội tiếp đường tròn và là một điểm của cung nhỏ Trên lấy điểm sao cho
Hỏi tam giác MBD là tam giác gì
So sánh hai tam giác và
Chứng minh rằng
Phương pháp giải:
Ta sử dụng kiến thức:
+) Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau.
Lời giải:
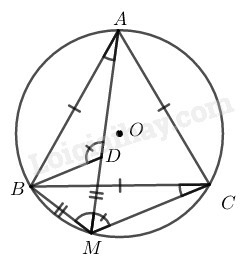
cân tại
( góc nội tiếp cùng chắn cung )
Mà (vì đều)
hay
Vậy đều
đều
đều
Từ và suy ra:
Xét và
(chứng minh trên)
(vì đều)
Suy ra:
(chứng minh trên)
Ta có: mà
Suy ra:
Bài 21 trang 102 SBT Toán 9 tập 2: Cho tam giác nội tiếp trong đường tròn tâm biết , . Lấy các điểm thuộc đường tròn tâm sao cho Hãy tính các góc của tam giác
Phương pháp giải:
Ta sử dụng kiến thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
Lời giải:
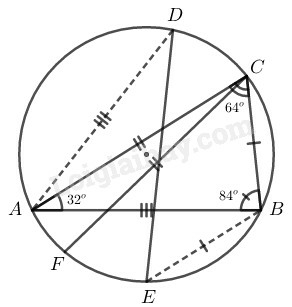
Xét đường tròn có:
(tính chất góc nội tiếp)
Ta có:
Mà (tính chất góc nội tiếp)
sđ
Lại có:
Trong ta có:
Mà (tính chất góc nội tiếp)
Lại có
Ta có: )
Bài 22 trang 102 SBT Toán 9 tập 2: Vẽ một tam giác vuông biết cạnh huyền là và đường cao ứng với cạnh huyền là
Phương pháp giải:
Ta sử dụng kiến thức:
+) Góc nội tiếp chắn nửa đường tròn là góc vuông.
Lời giải:
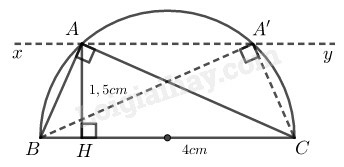
Cách vẽ:
– Vẽ đoạn
– Vẽ nửa đường tròn đường kính
– Vẽ đường thẳng nằm trên nửa mặt phẳng chứa nửa đường tròn và cách một khoảng bằng
– Đường thẳng cắt nửa đường tròn đường kính tại và Nối ta có hoặc cần vẽ.
Chứng minh:
Vì cách một khoảng nên đường thẳng cắt nửa đường tròn đường kính
Ta lại có nội tiếp trong nửa đường tròn đường kính nên
Có và
Vậy tam giác hoặc tam giác thỏa mãn đề bài.
Bài 23 trang 103 SBT Toán 9 tập 2: Cho tam giác cân nội tiếp đường tròn tâm Các đường phân giác của hai góc và cắt nhau ở và cắt đường tròn lần lượt ở và Chứng minh rằng tứ giác là một hình thoi.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Trong tam giác cân, hai góc kề cạnh đáy bằng nhau.
+) Trong một đường tròn, các góc nội tiếp chắn các cung bằng nhau thì bằng nhau.
+) Tứ giác có các cặp góc song song là hình bình hành.
+) Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
Lời giải:
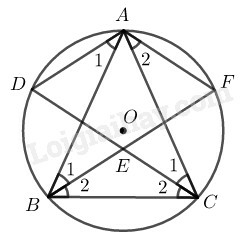
Vì cân tại
(tính chất tam giác cân)
Lại có:
là tia phân giác của
là tia phân giác của
Suy ra:
Suy ra:
Từ đó, đường tròn có: (hai góc nội tiếp chắn cung bằng nhau và )
(vì có cặp góc so le trong bằng nhau)
Hay
Tương tự: (hai góc nội tiếp chắn cung bằng nhau)
(vì có cặp góc ở vị trí so le trong bằng nhau)
Hay
Mà (chứng minh trên)
Từ và suy ra: Tứ giác là hình thoi
Bài tập bổ sung (trang 103 SBT Toán 9)
Bài 3.1 trang 103 SBT Toán 9 tập 2: Mỗi câu sau đây đúng hay sai
Góc nội tiếp là góc tạo bởi hai dây của đường tròn đó.
Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung.
Trong một đường tròn, hai góc nội tiếp không cùng chắn một cung thì không bằng nhau.
Trong một đường tròn, số đo của một góc nội tiếp bằng số đo cung bị chắn.
Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
Phương pháp giải:
Ta sử dụng kiến thức:
+) Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
+) Trong một đường tròn, các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung.
Lời giải:
Chọn câu đúng: Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
Các câu (A), (B), (C), (D) đều sai.
Bài 3.2 trang 103 SBT Toán 9 tập 2: Cho nửa đường tròn đường kính tâm Đường tròn tâm bán kính cắt nửa đường tròn đã cho tại Đường tròn tâm bán kính cắt nửa đường tròn đã cho tại Đường thẳng qua và song song với cắt nửa đường tròn đã cho tại
và có bằng nhau không Vì sao
Chứng minh song song với
Chứng minh vuông góc với
Tính số đo của .
So sánh hai cung và
Phương pháp giải:
Ta sử dụng kiến thức:
+) Trong một đường tròn, các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
+) Trong một đường tròn, góc nội tiếp chắn nửa đường tròn là góc vuông.
+) Tứ giác có bốn cạnh bằng nhau là hình thoi.
+) Trong hình thoi, hai đường chéo vuông góc.
+) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
Lời giải:
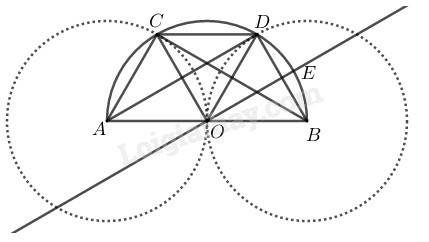
Trong đường tròn ta có:
( góc nội tiếp cùng chắn cung )
nội tiếp trong đường tròn có là đường kính nên vuông tại
(tính chất tam giác vuông)
Mà (bán kính đường tròn )
Suy ra:
đều
Ta có: nội tiếp trong đường tròn đường kính nên vuông tại
(tính chất tam giác vuông)
(bán kính đường tròn )
Suy ra:
đều
Mà
Suy ra:
Kết hợp với: (vì cùng bằng )
Suy ra: đều
(vì có cặp góc ở vị trí so le trong bằng nhau)
Ta có: đều (chứng minh trên)
đều (chứng minh trên)
Suy ra:
Vậy: tứ giác là hình thoi. Suy ra
đều (chứng minh trên) hay
Vì vuông tại
Vậy
(hai góc đồng vị)
mà (chứng minh trên)
Suy ra: Số đo cung gấp đôi số đo cung .