Giải Toán 9 Bài 5: Hệ số góc của đường thẳng y = ax + b ( a # 0)

Giải bài tập Toán 9 Bài 5: Hệ số góc của đường thẳng y = ax + b ( a # 0)

Trả lời câu hỏi giữa bài

Trả lời câu hỏi Bài 5 trang 56 Toán 9 Tập 1: Hình 11a) biểu diễn đồ thị của các hàm số (với hệ số $a>0$)

$y=0,5x+2;$       $y=x+2;$        $y=2x+2.$

Hình 11b) biểu diễn đồ thị của các hàm số (với hệ số $a<0$):

$y=-2x+2;$         $y=-x+2;$       $y=-0,5x+2.$

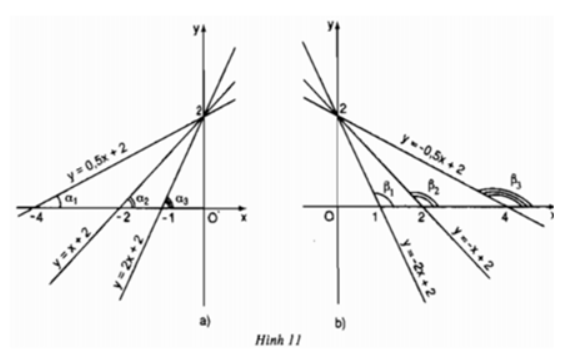
a) Hãy so sánh các góc ${\alpha }_1,{\alpha }_2,{\alpha }_3$ và so sánh các giá trị tương ứng của hệ số a trong các hàm số (trường hợp a > 0) rồi rút ra nhận xét.

b) Cũng làm tương tự như câu a) với trường hợp a > 0.

Phương pháp giải:

Quan sát hình vẽ để rút ra nhận xét.

Lời giải:

a) Ta có: ${\alpha }_1<{\alpha }_2<{\alpha }_3$ và các giá trị tương ứng của hệ số a trong các hàm số : $0,5<1<2$

Nhận xét: Khi hệ số a dương (a > 0) thì góc tạo bởi đường thẳng $y=ax+b$ và trục $Ox$ là góc nhọn, hệ số a càng lớn thì góc càng lớn nhưng vẫn nhỏ hơn 90o

b) Ta có: ${\beta }_1<{\beta }_2<{\beta }_3$ và các giá trị tương ứng của hệ số a trong các hàm số: $-2<-1<-0,5$

Nhận xét : Khi hệ số a âm (a < 0) thì góc tạo bởi đường thẳng $y=ax+b$ và trục $Ox$ là góc tù, hệ số a càng lớn thì góc càng lớn nhưng vẫn nhỏ hơn 180o.

Bài tập ( trang 58, 59 SGK Toán 9) 

Bài 27 trang 58 SGK Toán 9 Tập 1 :Cho hàm số bậc nhất  $y=ax+3$

a) Xác định hệ số góc $a$, biết rằng đồ thị của hàm số đi qua điểm $A(2;6)$.

b) Vẽ đồ thị của hàm số. 

Phương pháp giải:

a)  Thay tọa độ điểm $A$ vào công thức hàm số $y=ax+3$ ta tìm được $a$.

b) Cách vẽ đồ thị hàm số $y=ax+b,(a\ne 0)$: Đồ thị hàm số $y=ax+b(a\ne 0)$ là đường thẳng:

+) Cắt trục hoành tại điểm $A(-\frac{b}{a};0).$ 

+) Cắt trục tung tại điểm $B(0;b).$ 

Xác định tọa độ hai điểm $A$ và $B$ sau đó kẻ đường thẳng đi qua hai điểm đó ta được đồ thị hàm số  $y=ax+b(a\ne 0).$

Lời giải:
a)  $y=ax+3$   $(1)$ 

Theo giả thiết đồ thị hàm số đi qua điểm $A(2;6)$. Thay $x=2,y=6$ vào  $(1)$, ta được:

$6=2.a+3\iff 6-3=2a$

                      $\iff 3=2a$

                      $\iff a=\frac{3}{2}$

Vậy $a=\frac{3}{2}$,

b)  Vẽ đồ thị hàm số:   $y=\frac{3}{2}x+3$

Cho $x=2\Rightarrow y=\frac{3}{2}.2+3=3+3=6\Rightarrow A(2;6)$.

Cho $y=0\Rightarrow 0=\frac{3}{2}.x+3\Rightarrow x=-2\Rightarrow B(-2;0)$.

Đường thẳng đi qua hai điểm $A(2;6)$ và $B(-2;0)$ là đồ thị hàm số $y=\frac{3}{2}x+3$.

Đồ thị được vẽ như hình bên. 

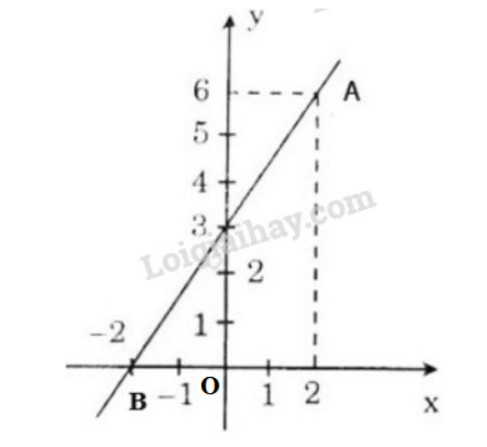
Bài 28 trang 58 SGK Toán 9 Tập 1 :Cho hàm số  $y=-2x+3.$ 

a) Vẽ đồ thị của hàm số.

b) Tính góc tạo bởi đường thẳng $y=-2x+3$ và trục $Ox$ (làm tròn đến phút).

Phương pháp giải:

a) Cách vẽ đồ thị hàm số $y=ax+b,(a\ne 0)$: Đồ thị hàm số $y=ax+b(a\ne 0)$ là đường thẳng:

+) Cắt trục hoành tại điểm $A(-\frac{b}{a};0).$ 

+) Cắt trục tung tại điểm $B(0;b).$ 

Xác định tọa độ hai điểm $A$ và $B$ sau đó kẻ đường thẳng đi qua hai điểm đó ta được đồ thị hàm số  $y=ax+b(a\ne 0).$

b) Góc tạo bởi đường thẳng $y=ax+b(a\ne 0)$ là góc $\alpha$ ta có: $tan\alpha =a.$

+) Với $a<0$, góc $\alpha$ là góc tù.

+) Với $a>0$, góc $\alpha$ là góc nhọn.

Sử dụng các công thức lượng giác để tính góc cần tìm: Cho tam giác $ABC$ vuông tại $A$. Khi đó: $\tan B=\frac{AC}{AB}.$

Lời giải:
a) Hàm số  $y=-2x+3.$

Cho $x=0\Rightarrow y=-2.0+3=0+3=3\Rightarrow A(0;3)$

Cho  $y=0\Rightarrow 0=-2.x+3\iff x=\frac{3}{2}\Rightarrow B\left(\frac{3}{2};0\right)$

Vẽ đường thẳng đi qua hai điểm $A(0;3)$ và  $B\left(\frac{3}{2};0\right)$ ta được đồ thị hàm số $y=-2x+3.$.

Đồ thị được vẽ như hình bên. 

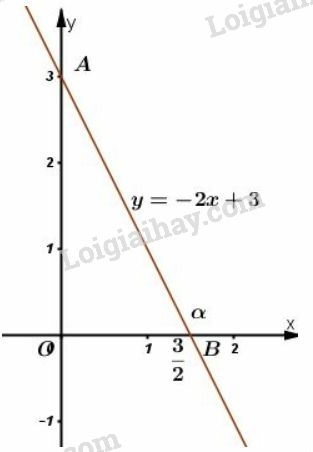
b) Gọi $\alpha$ là góc giữa đường thẳng $y=-2x+3$ và trục $Ox\Rightarrow \alpha =\widehat{ABx}$.

Xét tam giác vuông $OAB$ vuông tại $O$, ta có: 

                                 $\tan \widehat{OBA}=\frac{OA}{OB}=\frac{3}{\frac{3}{2}}=2$

Thực hiện bấm máy tính, ta được:

$\widehat{ABO}\approx {63}^0{26}^{\prime }$

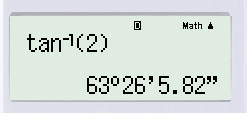
Lại có $\widehat{ABO}$ và $\widehat{ABx}$ là hai góc kề bù, tức là:

                              $\widehat{ABO}+\widehat{ABx}={180}^0$

                     $\iff \widehat{ABx}={180}^0-\widehat{ABO}$

                    $\iff \widehat{ABx}\approx {180}^0-{63}^0{26}^{\prime }$

                     $\iff \widehat{ABx}\approx {116}^0{34}^{\prime }$

Vậy $\alpha \approx {116}^0{34}^{\prime }$.

Bài 29 trang 59 SGK toán 9 Tập 1: Xác định hàm số bậc nhất $y=ax+b$ trong mỗi trường hợp sau: 

a) $a=2$ và đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng $1,5$.

b) $a=3$ và đồ thị của hàm số đi qua điểm $A(2;2)$.

c) Đồ thị của hàm số song song với đường thẳng $y=\sqrt{3}x$ và đi qua điểm $B\left(1;\sqrt{3}+5\right)$

Phương pháp giải:

a) Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng $x_0$ thì tung độ bằng $0$.  Tức là điểm $A(x_0;0)$ thuộc đồ thị hàm số. Thay tọa độ điểm $A$ vào công thức hàm số ta tìm được $b$.

b) Biết $a$, thay tọa độ điểm điểm $A$ vào phương trình đường thẳng $y=ax+b$ ta tìm được $b$.

c) Đồ thị hàm số $y=ax+b$ song song với đường thẳng $y=a^{\prime }x$ thì $a=a^{\prime };b\ne 0$. Thay tọa độ điểm $B$ vào phương trình ta tìm được $b$.

Lời giải: 

  Hàm số đã cho là $y=ax+b$.  $(1)$
 Theo giả thiết $a=2\Rightarrow y=2x+b.$   $(2)$

Vì đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng $1,5$ nên đồ thị hàm số đi qua $(1,5;0)$. Thay $x=1,5,y=0$ vào $(2)$, ta được:

$0=2.1,5+b$

$\iff 0=3+b$

$\iff b=-3$

Vậy hàm số đã cho là $y=2x-3.$

b) Theo giả thiết $a=3\Rightarrow y=3x+b$  $(3)$

 Vì đồ thị đi qua điểm $A(2;2)$. Thay $x=2,y=2$ vào $(3)$, ta được:

$2=3.2+b$

$\iff 2=6+b$

$\iff 2-6=b$

$\iff b=-4$

Vậy hàm số đã cho là $y=3x-4.$

c) Vì đồ thị hàm số đã cho $y=ax+b$ song song với đường thẳng $y=\sqrt{3}x$ nên $a=\sqrt{3};b\ne 0$.

Do đó hàm số đã cho có dạng: $y=\sqrt{3}x+b$ $(4)$

Vì đồ thị hàm số đã cho đi qua điểm $B\left(1;\sqrt{3}+5\right)$, nên thay $x=1,y=\sqrt{3}+5$ vào  $(4)$, ta được:

$\sqrt{3}+5=\sqrt{3}.1+b$

$\iff \sqrt{3}+5-\sqrt{3}=b$.

$\iff (\sqrt{3}-\sqrt{3})+5=b$.

$\iff b=5$ (thỏa mãn)

Vậy hàm số đã cho là $y=\sqrt{3}x+5$

Bài 30 trang 59 SGK Toán 9 Tập 1: a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số sau: 

$y=\frac{1}{2}x+2$;                                      $y=-x+2$

b) Gọi giao điểm của hai đường thẳng $y=\frac{1}{2}x+2$  và  $y=-x+2$ với trục hoành theo thứ tự là $A,B$ và gọi giao điểm của hai đường thẳng đó là $C$. Tính các góc của tam giác $ABC$ (làm tròn đến độ).

c) Tính chu vi và diện tích của tam giác $ABC$ (đơn vị đo trên các trục tọa độ là xentimét)

Phương pháp giải:

a) Cách vẽ đồ thị hàm số $y=ax+b,(a\ne 0)$: Đồ thị hàm số $y=ax+b(a\ne 0)$ là đường thẳng:

+) Cắt trục hoành tại điểm $A(-\frac{b}{a};0).$  

+) Cắt trục tung tại điểm $B(0;b).$

Xác định tọa độ hai điểm $A$ và $B$ sau đó kẻ đường thẳng đi qua hai điểm đó ta được đồ thị hàm số  $y=ax+b(a\ne 0).$

b) +) Phương trình hoành độ giao điểm của hai đường thẳng $y=ax+b$ và $y=a^{\prime }x+b^{\prime }$ là: $ax+b=a^{\prime }x+b^{\prime }$. Giải phương trình trên ta tìm được hoành độ giao điểm, thay hoành độ tìm được vào công thức hàm số tìm được tung độ giao điểm.

+) Đường thẳng $y=ax+b$ giao với trục hoành tại điểm có tọa độ là $A(-\frac{b}{a};0).$

+) Tính tỷ số lượng giác của các góc, từ đó tính số đo góc.

c) Sử dụng định lí Py-ta-go trong tam giác vuông để tính độ dài các cạnh:

           $\mathrm{\Delta }ABC$ vuông tại $A$ khi đó: $B{C}^2=A{C}^2+A{B}^2$

+ Chu vi $\mathrm{\Delta }ABC$ là: $C_{\mathrm{\Delta }ABC}=AB+BC+AC$

+ Diện tích $\mathrm{\Delta }ABC$ là: $S_{\mathrm{\Delta }ABC}=\frac{1}{2}.h.a$

trong đó: $h$ là độ dài đường cao, $a$ là độ dài cạnh ứng với đường cao.

Lời giải:
a) Đồ thị được vẽ như hình dưới:

+) Hàm số $y=\frac{1}{2}x+2$:     

     Cho $x=0\Rightarrow y=\frac{1}{2}.0+2=0+2=2\Rightarrow M(0;2)$.

     Cho $y=0\Rightarrow 0=\frac{1}{2}.x+2\Rightarrow x=-4\Rightarrow N(-4;0)$.

Đồ thị hàm số $y=\frac{1}{2}x+2$ là đường thẳng đi qua hai điểm $M(0;2)$ và $N(-4;0)$

+) Hàm số  $y=-x+2$:

     Cho $x=0\Rightarrow y=0+2=2\Rightarrow M(0;2)$.

     Cho $y=0\Rightarrow 0=-x+2\Rightarrow x=2\Rightarrow P(2;0)$.

Đồ thị hàm số $y=-x+2$   là đường thẳng đi qua hai điểm $M(0;2)$ và $P(2;0)$ 

      

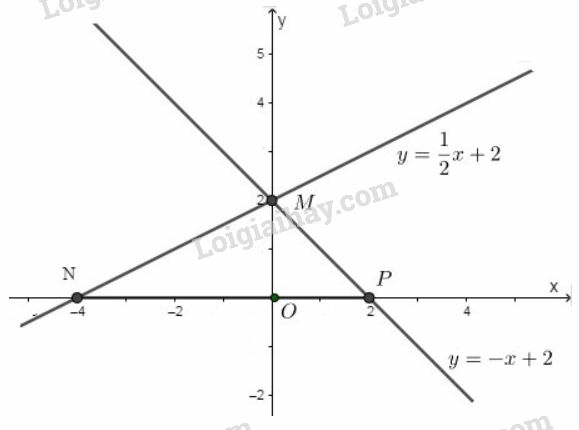
b) +) Hoành độ điểm $C$ là nghiệm của phương trình:

$\frac{1}{2}x+2=-x+2$

$\iff \frac{1}{2}x+x=2-2$

$\iff \frac{3}{2}x=0$

$\iff x=0$

Do đó tung độ của $C$ là: $y=0+2=2$. Vậy $C(0;2)\equiv M$.

 +) Vì $A$ thuộc trục hoành $Ox$ nên tung độ của $A$ bằng $0$. Thay $y=0$ vào $y=\frac{1}{2}x+2$, ta được:

$0=\frac{1}{2}x+2$

$\iff \frac{1}{2}x=-2$

$\iff x=-4$ 

Vậy $A(-4;0)\equiv N$.

+) Vì $B$ thuộc trục hoành $Ox$ nên tung độ của $B$ bằng $0$. Thay $y=0$ vào $y=-x+2$, ta được:

$0=-x+2$

$\iff x=2$

Vậy $B(2;0)\equiv P$.

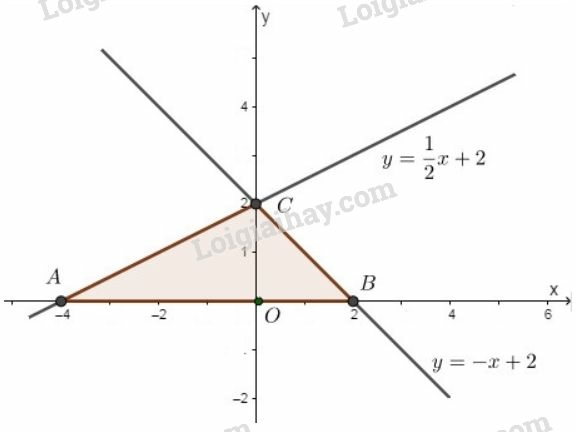
Ta có được $OA=4,OB=2,OC=2,$$AB=OA+OB=4+2=6$.

Ta có: $OB=OC$ nên tam giác $COB$ vuông cân tại $O$ ($O$ là gốc tọa độ) nên: $\hat{B}={45}^o$

Dùng định nghĩa tỉ số lượng giác đối với tam giác $AOC$ vuông tại $O$, ta có:

                         $\tan A=\frac{OC}{OA}=\frac{2}{4}=\frac{1}{2}$

Thực hiện bấm máy tính, ta được:  $\hat{A}\approx {27}^o$

Xét $\mathrm{\Delta }ABC$ có: $\hat{A}+\hat{B}+\hat{C}={180}^o$

                         $\iff \hat{C}={180}^o-\hat{A}-\hat{B}$

                         $\iff \hat{C}\approx {180}^o-{27}^o-{45}^o$

                         $\iff \hat{C}\approx {108}^o$

c) Ta có: $AB=6(cm)$

Xét tam giác vuông $OAC$ vuông tại $O$, theo định lí Py-ta-go, ta có:

                 $A{C}^2=A{O}^2+O{C}^2=4^2+2^2=16+4=20$

             $\Rightarrow AC=\sqrt{20}=2\sqrt{5}(cm)$

Xét tam giác vuông $OBC$ vuông tại $O$, ta có:

                  $B{C}^2=B{O}^2+O{C}^2=2^2+2^2=4+4=8$

              $\Rightarrow BC=\sqrt{8}=2\sqrt{2}(cm)$

$\mathrm{\Delta }OAC$ có $CO\mathrm{\perp }AB$ nên $CO$ là đường cao ứng với cạnh $AB$.

Chu vi tam giác là:

       $P=AB+BC+AC=6+2\sqrt{5}+2\sqrt{2}(cm)$

Diện tích tam giác là:

       $S=\frac{1}{2}.OC.AB=\frac{1}{2}.2.6=6(c{m}^2)$ 

Bài 31 trang 59 SGK Toán 9 Tập 1: a) Vẽ đồ thị của hàm số :

$y=x+1;y=\frac{1}{\sqrt{3}}x+\sqrt{3};y=\sqrt{3}x-\sqrt{3}$

b) Gọi  $\alpha ,\beta ,\gamma$  lần lượt là các góc tạo bởi các đường thẳng trên và trục Ox.

Chứng minh rằng $tg\alpha =1,tg\beta =\frac{1}{\sqrt{3}};tg\gamma =\sqrt{3}$

Tính số đo các góc $\alpha ,\beta ,\gamma .$

Phương pháp giải:

a) Cách vẽ đồ thị hàm số $y=ax+b,(a\ne 0)$: Đồ thị hàm số $y=ax+b(a\ne 0)$ là đường thẳng:

+) Cắt trục hoành tại điểm $A(-\frac{b}{a};0).$  

+) Cắt trục tung tại điểm $B(0;b).$

Xác định tọa độ hai điểm $A$ và $B$ sau đó kẻ đường thẳng đi qua hai điểm đó ta được đồ thị hàm số  $y=ax+b(a\ne 0).$

b) Góc tạo bởi đường thẳng $y=ax+b(a\ne 0)$ là góc $\alpha$ ta có: $tan\alpha =a.$

+) Với $a<0$, góc $\alpha$ là góc tù.

+) Với $a>0$, góc $\alpha$ là góc nhọn.

Hoặc sử dụng công thức lượng giác trong tam giác vuông:

      $\mathrm{\Delta }ABC$ vuông tại $A$ khi đó: $tanB=\frac{AC}{AB}$

Lời giải:

a)  

+ Hàm số $y=x+1$

   Cho $x=0\Rightarrow y=0+1=1\Rightarrow A(0;1)$

   Cho $x=-1\Rightarrow y=-1+1=0\Rightarrow B(-1;0)$

Đồ thị hàm số $y=x+1$ là đường thẳng đi qua hai điểm $A(0;1)$ và $B(-1;0)$

+ Hàm số $y=\frac{1}{\sqrt{3}}x+\sqrt{3}$

   Cho $x=-3\Rightarrow y=\frac{1}{\sqrt{3}}.(-3)+\sqrt{3}=0\Rightarrow D(-3;0)$

   Cho $x=0\Rightarrow y=\frac{1}{\sqrt{3}}.0+\sqrt{3}=\sqrt{3}\Rightarrow C(0;\sqrt{3})$

Đồ thị hàm $y=\frac{1}{\sqrt{3}}x+\sqrt{3}$ là đường thẳng đi qua hai điểm $D(-3;0)$ và $C(0;\sqrt{3})$

+ Hàm số $y=\sqrt{3}x-\sqrt{3}$

   Cho $x=0\Rightarrow y=\sqrt{3}.0-\sqrt{3}=-\sqrt{3}\Rightarrow E(0;-\sqrt{3})$

   Cho $x=1\Rightarrow y=\sqrt{3}.1-\sqrt{3}=0\Rightarrow F(1;0)$

Đồ thị hàm số $y=\sqrt{3}x-\sqrt{3}$ là đường thẳng đi qua hai điểm $E(0;-\sqrt{3})$ và $F(1;0)$

 

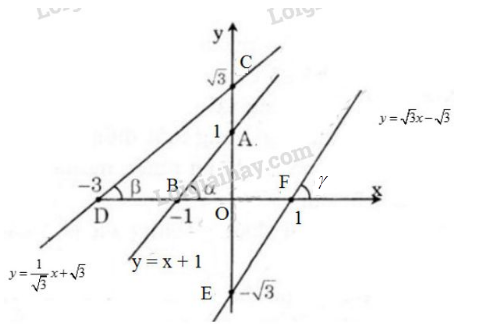
b)

Cách 1:

+ Đường thẳng $y=x+1$ có hệ số góc là $1$

Suy ra $tan\alpha =1\iff \alpha ={45}^o$

+ Đường thẳng $y=\frac{1}{\sqrt{3}}x+\sqrt{3}$ có hệ số góc là $\frac{1}{\sqrt{3}}$

Suy ra $tan\beta =\frac{1}{\sqrt{3}}\iff \beta ={30}^o$

+ Đường thẳng $y=\sqrt{3}x-\sqrt{3}$ có hệ số góc là $\sqrt{3}$

Suy ra $tan\gamma =\sqrt{3}\iff \alpha ={60}^o$

Cách 2:

+ Ta có:

$OA=OB=OF=1$, $OE=OC=\sqrt{3}$,  $OD=3$.

+ Xét $\mathrm{\Delta }OAB$ vuông tại $O$

               $\Rightarrow \tan \alpha =tanB=\frac{OA}{OB}=\frac{1}{1}=1$

               $\Rightarrow \alpha ={45}^o$  

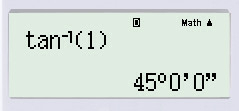
Thực hiện bấm máy tính: 

+ Xét $\mathrm{\Delta }ODC$ vuông tại $O$

                $\Rightarrow \tan \beta =tanD=\frac{OC}{OD}=\frac{\sqrt{3}}{3}$

                $\Rightarrow \beta ={30}^o$

+ Xét $\mathrm{\Delta }OEF$ vuông tại $O$

                $\Rightarrow \tan \beta =tan\widehat{OFE}=\frac{OE}{OF}=\frac{\sqrt{3}}{1}=\sqrt{3}$

                $\Rightarrow \gamma ={60}^o$

Lại có $\widehat{OFE}$ và $\gamma$ là hai góc đối đỉnh $\Rightarrow \widehat{OFE}=\gamma$.

Vậy $\gamma ={60}^o$.

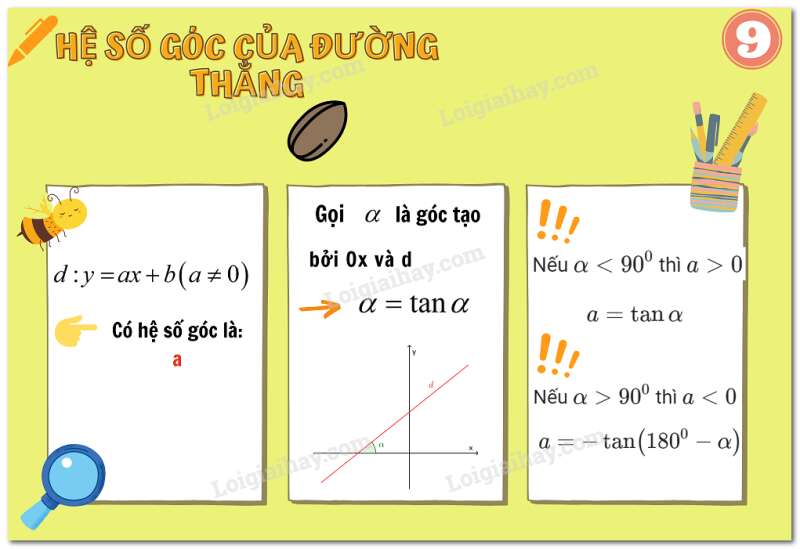
Lý thuyết Bài 5: Hệ số góc của đường thẳng y=ax + b ( a # 0)

1. Góc tạo bởi đường thẳng $y=ax+b(a\ne 0)$ và trục $Ox.$

Gọi $A$ là giao điểm của đường thẳng $d:y=ax+b$ với trục $Ox$ và $T$ là một điểm thuộc đường thẳng, nằm phía trên trục $Ox.$ Khi đó góc $\alpha =\widehat{TAx}$ được gọi là góc tạo bởi đường thẳng $d:y=ax+b$ và trục $Ox.$ 

 

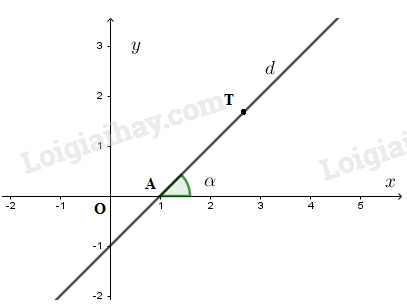
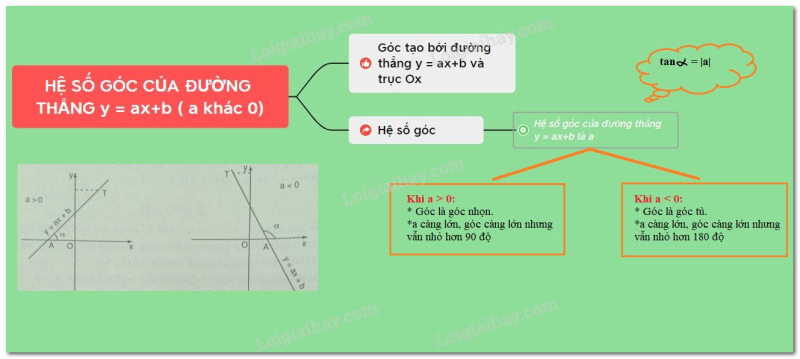
2. Hệ số góc của đường thẳng $y=ax+b(a\ne 0)$ 

+) Khi $a>0,$ góc tạo bởi đường thẳng $y=ax+b$ và trục $Ox$ là góc nhọn và nếu $a$ càng lớn thì góc đó càng lớn nhưng vẫn nhỏ hơn ${90}^0.$

+) Khi $a<0,$ góc tạo bởi đường thẳng $y=ax+b$ và trục $Ox$ là góc tù và nếu $|a|$ càng bé thì góc đó càng lớn nhưng vẫn nhỏ hơn ${180}^0.$

Như vậy, góc tạo bởi đường thẳng $d:y=ax+b$ và trục $Ox$ phụ thuộc vào $a.$

Người ta gọi $a$ là hệ số góc của đường thẳng $y=ax+b.$

Lưu ý:

+) Khi $a>0,$ ta có $\tan \alpha =a.$

+) Khi $a<0,$ ta có $\tan ({180}^0-\alpha )=-a.$

Từ đó tìm được số đo của góc ${180}^0-\alpha$ rồi suy ra số đo của góc $\alpha .$

+) Các đường thẳng có cùng hệ số $a$ ($a$ là hệ số của $x$) thì tạo với trục $Ox$ các góc bằng nhau.

3. Các dạng toán cơ bản

Dạng 1: Xác định hệ số góc của đường thẳng

Phương pháp:

Đường thẳng $(d)$ có phương trình $y=ax+b\left(a\ne 0\right)$ có $a$ là hệ số góc.

Ví dụ: Hệ số góc của đường thẳng $y=-2x+1$ là $a=-2$

Dạng 2: Tính góc tạo bởi tia $Ox$ và đường thẳng $(d).$

Phương pháp:

Gọi $\alpha$ là góc tạo bởi tia $Ox$ và $d.$ Ta có: $a=\tan \alpha$

Ví dụ: Góc tạo bởi tia $Ox$ và đường thẳng $(d):y=\sqrt{3}x+1$ là $\alpha$

Khi đó: $\tan \alpha =\sqrt{3}$ nên $\alpha ={60}^0$

Dạng 3. Viết phương trình đường thẳng hoặc tìm tham số m khi biết hệ số góc

Phương pháp:

Gọi phương trình  đường thẳng cần tìm là $y=ax+b\left(a\ne 0\right)$.

Dựa vào lý thuyết về hệ số góc để tìm $a$. Từ đó, sử dụng dữ kiện còn lại của đề bài để tìm $b$.