Giải Toán 9 Bài 2: Hàm số bậc nhất

Giải bài tập Toán 9 Bài 2: Hàm số bậc nhất

Trả lời câu hỏi giữa bài 

Trả lời câu hỏi 1  trang 46 SGK Toán 9 Tập 1 :Hãy điền vào chỗ trống (…) cho đúng

Sau 1 giờ, ô tô đi được: …

Sau t giờ, ô tô đi được: …

Sau t giờ, ô tô cách trung tâm Hà Nội là: s = …

Phương pháp giải:

Sử dụng công thức $S=v.t$ với $S$ là quãng đường đi được, $v$ là vận tốc và $t$ là thời gian.

Lời giải: 

Sau 1 giờ, ô tô đi được: 50 (km)

Sau t giờ, ô tô đi được: 50.t (km)

Sau t giờ, ô tô cách trung tâm Hà Nội là: s = 50.t + 8 (km)

Trả lời câu hỏi 2  trang 47 SGK Toán 9 Tập 1 :Cho s= 50.t – 8 . Tính các giá trị tương ứng của s khi cho t lần lượt lấy các giá trị 1 giờ; 2 giờ; 3 giờ; 4 giờ; … rồi giải thích tại sao s là hàm số của t ?

Lời giải:
Với t = 1, ta có $s=50.t-8=50.1-8=42$ (km)

Với t = 2, ta có $s=50.t-8=50.2-8=92$ (km)

Với t = 3, ta có $s=50.t-8=50.3-8=142$ (km)

Với t = 4, ta có $s=50.t-8=50.4-8=192$ (km)

…….

s là hàm số của t vì đại lượng s phụ thuộc vào đại lượng thay đổi t và với mỗi giá trị của t ta chỉ xác định được một giá trị tương ứng của s. 

Trả lời câu hỏi 3 trang 47 SGK Toán 9 Tập 1 :Cho hàm số bậc nhất $y=f\left(x\right)=3x+1$

Cho $x$ hai giá trị bất kì $x_1;x_2$ sao cho $x_1<x_2.$ Hãy chứng minh $f\left(x_1\right)<f\left(x_2\right)$ rồi rút ra kết luận hàm số đồng biến trên

Phương pháp giải:

Sử dụng định nghĩa: 

Cho hàm số $y=f\left(x\right)$ xác định trên $\mathbb{R}$ và $x_1;x_2\in \mathbb{R}$ sao cho $x_1<x_2$ mà $f\left(x_1\right)<f\left(x_2\right)$ thì hàm số đồng biến trên $\mathbb{R}.$

Lời giải:

Ta có $f\left(x_1\right)=3x_1+1;f\left(x_2\right)=3x_2+1$

Vì $x_1<x_2$ nên $x_1-x_2<0$

Xét $f\left(x_1\right)-f\left(x_2\right)=3x_1+1-\left(3x_2+1\right)$ $=3x_1-3x_2=3\left(x_1-x_2\right)<0$ hay $f\left(x_1\right)<f\left(x_2\right)$

Vậy hàm số $y=3x+1$ là hàm số đồng bến trên $\mathbb{R}.$  

Trả lời câu hỏi 4 trang 47 SGK Toán 9 Tập 1 :Cho ví dụ về hàm số bậc nhất trong các trường hợp sau:

a) Hàm số đồng biến.

b) Hàm số nghịch biến. 

Phương pháp giải:

Hàm số bậc nhất $y=ax+b\left(a\ne 0\right)$

+ Đồng biến trên $\mathbb{R}$ khi $a>0.$

+ Nghịch biến trên $\mathbb{R}$ khi $a<0$. 

Lời giải:
a) Ví dụ: Các hàm số $y=2x-3;y=\frac{1}{2}x;y=5x+1;...$ là các hàm số đồng biến.
b) Ví dụ: Các hàm số $y=-3x;y=-\frac{1}{3}x+2;y=-x-5;...$ là các hàm số nghịch biến.

Bài tập ( trang 48 SGK Toán 9)
Bài 8 trang 48 SGK Toán 9 Tập 1 :Trong các hàm số sau, hàm số nào là hàm số bậc nhất? Hãy xác định các hệ số $a,b$ của chúng và xét xem hàm số bậc nhất nào đồng biến, nghịch biến. 

a) $y=1-5x$;                                         b) $y=-0,5x$;

c) $y=\sqrt{2}\left(x-1\right)+\sqrt{3}$                    d) $y=2x^2+3$.

Phương pháp giải:

+) Hàm số bậc nhất là hàm số được cho bởi công thức: 

                                  $y=ax+b$;   $a,b$ là số cho trước,  $a\ne 0$.

+) Hàm số bậc nhất xác định với mọi giá trị của $x$ trên $\mathbb{R}$ và có tính chất sau:

      a) Đồng biến trên $\mathbb{R}$  khi $a>0$.

      b) Nghịch biến trên $\mathbb{R}$  khi $a<0$

Lời giải:
a) Ta có: 

$y=1-5x\iff y=-5x+1$

$\Rightarrow$ hàm số trên là một hàm số bậc nhất với $a=-5,b=1$.

Vì $a=-5<0$ nên hàm số trên nghịch biến.

b) Ta có:

$y=-0,5x\iff y=-0,5x+0$

$\Rightarrow$ hàm số trên là một hàm bậc nhất với $a=-0,5,b=0$.

 Vì $a=-0,5<0$ nên  hàm số nghịch biến.

c) Ta có:

$y=\sqrt{2}\left(x-1\right)+\sqrt{3}\iff y=\sqrt{2}x-\sqrt{2}+\sqrt{3}$

                                      $\iff y=\sqrt{2}x+(\sqrt{3}-\sqrt{2})$

$\Rightarrow$ hàm số trên là hàm số bậc nhất với $a=\sqrt{2},b=\sqrt{3}-\sqrt{2}$.

Vì $a=\sqrt{2}>0$ nên hàm số trên đồng biến.

d) Ta có:

$y=2x^2+3$ trong đó $x$ có bậc là $2$.

$\Rightarrow$ hàm số trên không phải là một hàm số bậc nhất vì nó không có dạng $y=ax+b$, với $a\ne 0$.

Bài 9 trang 48 SGK Toán 9 Tập 1 :Cho hàm số bậc nhất $y=(m-2)x+3$. Tìm các giá trị của $m$ để hàm số:

a) Đồng biến;

b) Nghịch biến.

Phương pháp giải:

+ Hàm số bậc nhất xác định với mọi giá trị của $x$ trên $\mathbb{R}$ và có tính chất sau:

      a) Đồng biến trên $\mathbb{R}$  khi $a>0$.

      b) Nghịch biến trên $\mathbb{R}$  khi $a<0$.

Lời giải:
Hàm số: $y=(m-2)x+3$ có $a=m-2,b=3$  

a) Hàm số: $y=(m-2)x+3$ đồng biến trên $\mathbb{R}$ khi: 

$a>0\iff m-2>0\iff m>2$

Vậy với $m>2$ thì hàm số đồng biến.

b)  Hàm số: $y=(m-2)x+3$ nghịch biến trên $\mathbb{R}$ khi: 

$a<0\iff m-2<0\iff m<2$

Vậy với $m<2$ thì hàm số nghịch biến.

Bài 10 trang 48 SGK Toán 9 Tập 1 :Một hình chữ nhật có các kích thước là $20cm$ và $30cm$. Người ta bớt mỗi kích thước của hình đó đi $x$ $(cm)$ được hình chữ nhật mới có chu vi là $y$ $(cm)$. Hãy lập công thức tính $y$ theo $x$.

Phương pháp giải:

Hình chữ nhật có chiều rộng và chiều dài lần lượt là $a,b$ có chu vi là: $C=(a+b).2$

Lời giải:
Chiều rộng và chiều dài hình chữ nhật ban đầu lần lượt là $20cm$ và $30cm$.

Khi bớt mỗi kích thước $x$ $(cm)$ thì hình chữ nhật mới  có chiều rộng và chiều dài lần lượt là: $20-x$  $(cm)$ và $30-x$  $(cm)$. 

Khi đó chu vi $y$ của hình chữ nhật là:

$y=2\left[(20-x)+(30-x)\right]$

$\iff y=2(20-x+30-x)$

$\iff y=2(50-2x)$

$\iff y=2.50-2.2x$

$\iff y=100-4x$ $(cm)$

Bài 11 trang 48 SGK Toán 9 Tập 1 :Hãy biểu biễn các điểm sau trên mặt phẳng tọa độ:

$A(-3;0)$,  $B(-1;1)$,  $C(0;3)$,   $D(1;1)$, 

$E(3;0)$,   $F(1;-1)$,  $G(0;-3)$,  $H(-1;-1)$.

Phương pháp giải: 

+) Điểm $A(x_0;y_0)$ thì hoành độ là $x_0$ và tung độ là $y_0$.

+) Điểm $B(0;b)$ nằm trên trục tung, tung độ là $b$.

+) Điểm $C(c;0)$ nằm trên trục hoành, tung độ là $c$.

Lời giải:

+) Điểm $A(-3;0)\Rightarrow$ hoành độ là $-3$ và tung độ là

$\Rightarrow$ điểm $A$ nằm trên trục hoành, hoành độ là $-3$.

+) Điểm $B(-1;1)\Rightarrow$ hoành độ là $-1$ và tung độ là $1$

+) Điểm $C(0;3)\Rightarrow$ hoành độ là $0$ và tung độ là $3$

$\Rightarrow$ điểm $C$ nằm trên trục tung, tung độ là $3$.

+) Điểm $D(1;1)\Rightarrow$ hoành độ là $1$ và tung độ là $1$

+) Điểm $E(3;0)\Rightarrow$ hoành độ là $3$ và tung độ là $0$$0$

$\Rightarrow$ điểm $E$ nằm trên trục hoành, hoành độ là $3$.

+) Điểm $F(1;-1)\Rightarrow$ hoành độ là $1$ và tung độ là $-1$

+) Điểm $G(0;-3)\Rightarrow$ hoành độ là $0$ và tung độ là $-3$

$\Rightarrow$ điểm $C$ nằm trên trục tung, tung độ là $-3$.

+) Điểm $H(-1;-1)\Rightarrow$ hoành độ là $-1$ và tung độ là $-1$

Xem hình sau:

 

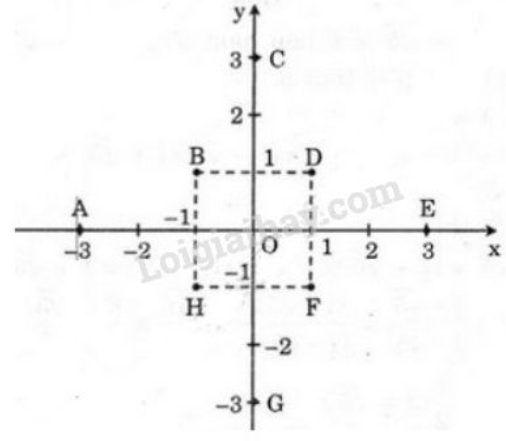
Bài 12 trang 48 SGK Toán 9 Tập 1 :Cho hàm số bậc nhất $y=ax+3$. Tìm hệ số $a$, biết rằng khi $x=1$ thì $y=2,5$. 
Phương pháp giải:
Hàm số $y=ax+b$ đi qua điểm $A(x_0;y_0)$ thì tọa độ điểm $A$ thỏa mãn công thức hàm số. Tức là: $y_0=a.x_0+b$.

Lời giải:

Thay $x=1,y=2,5$ vào công thức hàm số $y=ax+3$, ta được:

$2,5=1.a+3$

$\iff 2,5=a+3$

$\iff 2,5-3=a$

$\iff a=-0,5$.

Vậy $a=-0,5$ và hàm số đó là $y=-0,5x+3$.

Bài 13 trang 48 SGK Toán 9 Tập 1 :Với những giá trị nào của $m$ thì mỗi hàm số sau là hàm số bậc nhất ?

a) $y=\sqrt{5-m}(x-1)$;

b) $y=\frac{m+1}{m-1}x+3,5$

Phương pháp giải:

+) Hàm số $y=ax+b$ là hàm bậc nhất nếu $a\ne 0$.

+) Điều kiện để căn thức $\sqrt{A}$ có nghĩa là $A\ge 0$.

+) Phân thức $\frac{A}{B}$ có nghĩa khi $B\ne 0$. 

Lời giải:

 a) Ta có $y=\sqrt{5-m}(x-1)\iff y=\sqrt{5-m}.x-\sqrt{5-m}$

     $\Rightarrow$ Hệ số là $a=\sqrt{5-m}$.

Điều kiện để  $y=\sqrt{5-m}.x-\sqrt{5-m}$ là hàm số hàm bậc nhất là: 

$\{\begin{array}{c}\sqrt{5-m}\ne 0\hfill \\ 5-m\ge 0\hfill \end{array}\iff \{\begin{array}{c}5-m\ne 0\hfill \\ 5-m\ge 0\hfill \end{array}$

$\iff 5-m>0\iff m<5$

Vậy $m<5$ thì hàm số đã cho là hàm số bậc nhất.

b) Ta có: $y=\frac{m+1}{m-1}x+3,5\Rightarrow$ Hệ số $a=\frac{m+1}{m-1}$ 

Điều kiện để hàm số $y=\frac{m+1}{m-1}x+3,5$ là hàm bậc nhất là: 

$\{\begin{array}{c}\frac{m+1}{m-1}\ne 0\hfill \\ m-1\ne 0\hfill \end{array}\iff \{\begin{array}{c}m+1\ne 0\hfill \\ m-1\ne 0\hfill \end{array}\iff \{\begin{array}{c}m\ne -1\hfill \\ m\ne 1\hfill \end{array}$

Vậy $m\ne \pm 1$ thì hàm số đã cho là hàm số bậc nhất.

Bài 14 trang 48 SGK Toán 9 Tập 1 :Cho hàm số bậc nhất $y=(1-\sqrt{5})x-1$.

a) Hàm số trên là đồng biến hay nghịch biến trên $\mathbb{R}$ ? Vì sao ?

b) Tính giá trị của $y$ khi $x=1+\sqrt{5}$;

c) Tính giá trị của $x$ khi $y=\sqrt{5}$.

Phương pháp giải:

a) +) Hàm số bậc nhất $y=ax+b$ xác định với mọi giá trị của $x$ trên $\mathbb{R}$

  –  Đồng biến trên $\mathbb{R}$  khi $a>0$. 

  –  Nghịch biến trên $\mathbb{R}$  khi $a<0$.

+) Sử dụng định lí so sánh hai căn bậc hai số học của hai số không âm:

            $a<b\iff \sqrt{a}<\sqrt{b},$  với $a,b\ge 0$.

b) +) Thay $x_0$ vào công thức hàm số $y=ax+b$ tính được giá trị của hàm số: $y_0=a{x}_0+b$.

     +) Sử dụng hằng đẳng thức: $a^2-b^2=(a-b)(a+b).$

c) +) Thay $x_0$ vào công thức hàm số $y=ax+b$ tính được giá trị của hàm số: $y_0=a{x}_0+b$.

     +) Sử dụng hằng đẳng thức:

            $(a+b{)}^2=a^2+2ab+b^2$.

            $a^2-b^2=(a-b)(a+b).$

+) Sử dụng công thức trục căn thức ở mẫu:

        $\frac{C}{\sqrt{A}\pm B}=\frac{C(\sqrt{A}\mp B)}{A-B^2}$

Lời giải: 

a) Hàm số $y=(1-\sqrt{5})x-1$ có hệ số $a=1-\sqrt{5}<0$

(Vì: $1<5\iff \sqrt{1}<\sqrt{5}$ $\iff 1<\sqrt{5}$$\iff 1-\sqrt{5}<0)$

Vậy hàm số $y=(1-\sqrt{5})x-1$ nghịch biến trên $\mathbb{R}$ (vì hệ số $a$ âm).

b) 

Thay $x=1+\sqrt{5}$ vào công thức của hàm số đã cho, ta được: 

           $y=(1-\sqrt{5})(1+\sqrt{5})-1$

       $\iff y=[1^2-(\sqrt{5}{)}^2]-1$

      $\iff y=(1-5)-1$

      $\iff y=-4-1$

      $\iff y=-5$

Vậy $x=1+\sqrt{5}$ thì $y=-5$.

c) Ta có:

Thay $y=\sqrt{5}$ vào công thức của hàm số, ta được:

$\sqrt{5}=(1-\sqrt{5})x-1$

$\iff (1-\sqrt{5})x=\sqrt{5}+1$

$\iff x=\frac{\sqrt{5}+1}{1-\sqrt{5}}$

$\iff x=\frac{(\sqrt{5}+1)(\sqrt{5}+1)}{(1-\sqrt{5})(\sqrt{5}+1)}$

$\iff x=\frac{(\sqrt{5}+1{)}^2}{1^2-(\sqrt{5}{)}^2}$

$\iff x=\frac{(\sqrt{5}{)}^2+2\sqrt{5}+1}{1-5}$

$\iff x=\frac{5+2\sqrt{5}+1}{-4}$

$\iff x=-\frac{6+2\sqrt{5}}{4}$

$\iff x=-\frac{2(3+\sqrt{5})}{2.2}$

$\iff x=-\frac{3+\sqrt{5}}{2}$

Vậy $y=\sqrt{5}$ thì $x=-\frac{3+\sqrt{5}}{2}$.

Lý thuyết Bài 2: Hàm số bậc nhất

1. Hàm số bậc nhất

Định nghĩa hàm số bậc nhất

Hàm số bậc nhất là hàm số được cho bởi công thức $y=ax+b$ trong đó $a,b$ là các số cho trước và $a\ne 0$.

Khi $b=0$ hàm số có dạng $y=ax$.

Tính chất

Hàm số bậc nhất $y=ax+b$ xác định với mọi giá trị của $x$ thuộc $\mathbb{R}$ và có tính chất sau

– Đồng biến trên $\mathbb{R}$ nếu $a>0$.

– Nghịch biến trên $\mathbb{R}$ nếu $a<0$

2. Các dạng toán thường gặp

Dạng 1: Nhận dạng hàm số bậc nhất

Phương pháp:

Hàm số bậc nhất là hàm số có dạng $y=ax+b\left(a\ne 0\right)$.

Dạng 2: Tìm $m$ để hàm số đồng biến, nghịch biến

Phương pháp:

Ta có hàm số bậc nhất $y=ax+b,\left(a\ne 0\right)$

– Đồng biến trên $\mathbb{R}$ nếu $a>0$.

– Nghịch biến trên $\mathbb{R}$ nếu $a<0$.