Bài tập Toán 9 Chương 1 Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông
A. Bài tập Một số hệ thức về cạnh và góc trong tam giác vuông
I. Bài tập trắc nghiệm
Câu 1: Cho tam giác MNP vuông tại N. Hệ thức nào sau đây là đúng?
A. MN = MP.sinP
B. MN = MP.cosP
C. MN = MP.tanP
D. MN = MP.cotP
Lời giải:
Ta có:
Chọn đáp án A
Câu 2: Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Chọn khẳng định sai?
A. b = a.sinB = a.cosC
B. a = c.tanB = c.cotC
C. a2 = b2 + c2
D. c = a.sinC = a.cosB
Lời giải:
Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Ta có:
+ Theo định lý Pytago ta có a2 = b2 + c2 nên C đúng
+ Theo hệ thức về cạnh và góc trong tam giác vuông ta có:
b = asinB = acosC; c = asinC = acosB; b = ctanB = ccotC; c = btanC = bcotB
Nên A, D đúng
Chọn đáp án B
Câu 3: Cho tam giác ABC vuông tại A có AC = 10 cm, C^= 30°. Tính
Lời giải:
Xét tam giác ABC vuông tại A có
Chọn đáp án D
Câu 4: Cho tam giác ABC vuông tại A có BC = 12 cm, B^= 40°. Tính (làm tròn đến chữ số thập phân thứ 2)
Lời giải:
Chọn đáp án C
Câu 5: Cho tam giác ABC vuông tại A có BC = 15 cm, AB = 12 cm. Tính AC, B
Lời giải:
Chọn đáp án B
Câu 6: Tam giác ABC vuông tại A ; đường cao AH; biết HB = 25cm; HC = 64 cm. Tính góc B
A. 42°
B. 32°
C. 51°
D. 58°
Lời giải:
Ta có: BC = HB + HC = 25 + 64 = 89 cm
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:
Chọn đáp án C.
Câu 7: Cho tam giác ABC vuông tại A có BC = 72 cm và góc B = 58° . Tính AB và AC ?
A. 38,15 và 61,06
B. 36,06 và 62,01
C. 37,09 và 60,19
D. 39,01 và 62,93
Lời giải:
Ta có:
Chọn đáp án A.
Câu 8: Cho tam giác ABC vuông tại A biết AC = 21 cm và AB = 18 cm. Tìm khẳng định sai ?
Lời giải:
Áp dụng định lí pytago ta có:
Chọn đáp án C.
Câu 9: Cho tam giác MNP vuông tại M có MN = 4 và B^= 30° . Tìm khẳng định sai trong các khẳng định sau?
Lời giải:
Áp dụng hệ thức về cạnh và góc trong tam giác vuông ta có:
Chọn đáp án D.
Câu 10: Cho tam giác ABC vuông tại A có đường cao AH và AB = 12 cm; AC = 16 cm.
Tìm khẳng định sai trong các khẳng định sau?
Lời giải:
Áp dụng định lí Pytago ta có:
BC2 = AB2 + AC2 = 122 + 162 = 400 ⇒ BC = 20 cm
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:
Câu 11: Cho tam giác ABC vuông tại A có BC = 26cm, AB = 10cm. (làm tròn đến độ)
Lời giải:
Đáp án cần chọn là: C
Câu 12: Cho tam giác ABC có AB = 16, AC = 14 và . Tính BC
A. BC = 10
B. BC = 11
C. BC = 9
D. BC = 12
Lời giải:
Áp dụng định lý Py-ta-go vào tam giác vuông AHC ta có:
Suy ra HC = 2.
Vậy BC = CH + HB = 2 + 8 = 10
Đáp án cần chọn là: A
Câu 13: Cho tam giác ABC có AB = 12, AC = 15 và . Tính BC
Lời giải:
Áp dụng định lý Py-ta-go vào tam giác vuông AHC ta có:
Đáp án cần chọn là: B
Câu 14: Cho tam giác ABC có Diện tích tam giác ABC gần nhất với giá trị nào dưới đây?
A. 4
B. 5
C. 7
D. 8
Lời giải:
Kẻ đường cao AD
Xét tam giác vuông ACD, có AD = AC. sin C = 3,5. sin 50o ≈ 2,68cm
CD = AC. cos C = 3,5. cos 50o ≈ 2,25cm
Xét tam giác vuông ABD có BD = AD. cot B ≈ 2,68. cot 60o ≈ 1,55cm
Suy ra BC = BD + CD = 3,8
Đáp án cần chọn là: B
Câu 15: Cho tam giác ABC có Diện tích tam giác ABC gần nhất với giá trị nào dưới đây? (làm tròn đến chữ số thập phân thứ hai)
A. 4
B. 5
C. 6
D. 8
Lời giải:
Kẻ đường cao AD
Xét tam giác vuông ACD, có AD = AC.sin C = 4,5. sin 35o ≈ 2,58 cm
CD = AC. cos C = 4,5. cos 35o ≈ 3,69 cm
Xét tam giác vuông ABD, có BD = AD. cot B ≈ 2,58. cot 70o ≈ 0,94 cm
Suy ra BC = BD + DC = 0,94 + 3,69 = 4,63
Đáp án cần chọn là: C
II. Bài tập tự luận có lời giải
Câu 1: Cho tam giác ABC có AB = 16, AC = 14 và ∠B = 60°.
a) Tính độ dài cạnh BC.
b) Tính diện tích tam giác ABC.
Lời giải:
a) Kẻ đường cao AH.
Xét tam giác vuông ABH, ta có: BH = AB.cosB = AB.cos60° = 16.(1/2) = 8.
AH = AB.sinB = AB.sin60° = 16.(√3)/2 = 8√3
Áp dụng định lý Py – ta – go vào tam giác vuông AHC ta có:
HC2 = AC2 – AH2 = 142 – (8√3)2 = 196 – 192 = 4. Suy ra HC = 2.
Vậy BC = CH + HB = 2 + 8 = 10
b) Ta có:
Câu 2: Một con thuyền băng qua một khúc sông với vận tốc là 3 km/h trong vòng 6 phút. Biết rằng hướng thuyền đi tạo với bờ một góc 60 độ. Tính chiều dài (m) của khúc sông đó.
Lời giải:
Ta giải bài toán thông qua hình vẽ trên
Nhận thấy ∠BAC = 30o
Ta đổi: 3(km/h) = 5/6(m/s); 6 phút = 360 giây
Khi đó ta có: S = (5/6). 360 = 300(m)
III. Bài tập vận dụng
Câu 1: Tính diện tích tam giác ABC biết bán kính đường tròn ngoại tiếp tam giác ABC là R.
Câu 2: Cho tam giác ABC với các đỉnh A, B, C và các cạnh đối diện với các đỉnh tương ứng là: a, b, c. Chứng minh rằng:
a) a2 = b2 + c2 – 2bccosA
b) Gọi D là chân đường phân giác trong góc A . Chứng minh:
B. Lý thuyết Một số hệ thức về cạnh và góc trong tam giác vuông
Định lí. Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
+ Cạnh huyền nhân với sin góc đối hay nhân với côsin góc kề.
+ Cạnh góc vuông kia nhân với tan của góc đối hay nhân với côtang của góc kề.
Ví dụ. Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c.
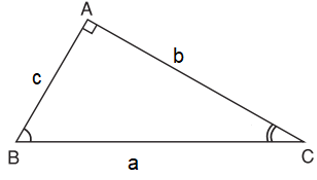
Khi đó, a là độ dài cạnh huyền;
b và c là độ dài hai cạnh góc vuông.
Do đó: b = a.sin B = a.cos C; c = a.sin C = a.cos B;
b = c.tan B = c.cot C; c = b.tan C = b.cot C.
Xem thêm