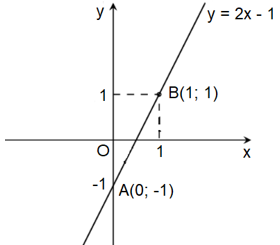50 Bài tập Đồ thị của hàm số y = ax + b (có đáp án)- Toán 9

Bài tập Toán 9 Chương 2 Bài 4: Đồ thị của hàm số y = ax + b

A. Bài tập Đồ thị của hàm số y = ax + b

I. Bài tập trắc nghiệm

Câu 1: Chọn khẳng định đúng về đồ thị hàm số y = ax + b (a ≠ 0) .

A. Là đường thẳng đi qua gốc tọa độ

B. Là đường thẳng song song với trục hoành

C. Là đường thẳng đi qua hai điểm  với b ≠ 0

D. Là đường cong đi qua gốc tọa độ

Lời giải:

Đồ thị hàm số y = ax + b (a ≠ 0) là một đường thẳng

Trường hợp 1: Nếu b = 0 ta có hàm số y = ax .

Đồ thị y = ax là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm A(1; a) .

Trường hợp 2: Nếu b ≠ 0 thì đồ thị y = ax là đường thẳng đi qua các điểm .

Chọn đáp án C.

Câu 2: Trong các hình vẽ sau, hình vẽ nào là đồ thị hàm số y = 2x + 1

A. Hình 4

B. Hình 2

C. Hình 3

D. Hình 1

Lời giải:

* Cho x = 0 ⇒ y = 1 ta được điểm A(0; 1) thuộc trục tung

Cho x = 1 ⇒ y = 3 ta được điểm B (1; 3)

*Đồ thị hàm số y = 2x + 1 đi qua hai điểm có tọa độ (0; 1) và (1; 3) nên hình 1 là đồ thị hàm số y = 2x + 1

Chọn đáp án D.

Câu 3: Đồ thị hàm số  đi qua điểm nào dưới đây:

Lời giải:

Chọn đáp án C.

Câu 4: Cho hai đường thẳng d1 = 2x -2 và d2 = 3 – 4x . Tung độ giao điểm của d1; d2 có tọa độ là:

Lời giải:

Chọn đáp án A.

Câu 5: Cho đường thẳng  . Giao điểm của với trục tung là:

Lời giải:

Chọn đáp án D.

Câu 6: Cho hai đường thẳng d1: y = 2x + 4 và d2: y = -x + 7. Tìm tọa độ giao điểm của hai đồ thị?

A. (1; 6)

B. (2 ; 8)

C. ( -1 ;2)

D. ( -2; 0)

Lời giải:

Phương trình hoành độ giao điểm của hai đồ thị:

2x + 4 = -x + 7

⇒ 2x + x = 7 -4

⇒ 3x = 3 ⇔ x = 1

Thay x = 1 vào phương trình đường thẳng y = 2x + 4 ta được: y = 2.1+ 4 = 6

Do đó, hai đồ thị đã cho cắt nhau tại A(1; 6)

Chọn đáp án A.

Câu 7: Biết rằng với x = 2 thì hàm số y = 2x + b có giá trị là 10. Tìm b?

A. b = 3

B. b = 6

C. b = -3

D. b = 2

Lời giải:

Thay x = 2; y = 10 vào y = 2x + b ta được:

10 = 2.2 + b

Suy ra: b = 6

Chọn đáp án C.

Câu 8: Biết rằng đồ thị hàm số y = ax – 10 đi qua điểm A( 1; -8). Tìm a?

A. 8

B.12

C. -8

D. 2

Lời giải:

Vì đồ thị hàm số đã cho đi qua A(1; -8) nên ta thay x = 1; y = -8 vào y = ax -10 ta được:

-8 = a.1 – 10 ⇔ a = 2

Chọn đáp án D.

Câu 9: Cho hàm số y = 3x + 12. Hỏi đồ thị hàm số cắt trục hoành tại điểm nào?

A. ( -4; 0)

B. (0;12)

C. (0; 4)

D. (12; 0)

Lời giải:

Cho y = 0 ⇒ 3x + 12 = 0 ⇔ x = -4

Do đó, đồ thị hàm số y = 3x + 12 cắt trục hoành tại điểm A( -4; 0)

Chọn đáp án A.

Câu 10: Cho đồ thị hàm số y = -x + 4. Đồ thị hàm số cắt trục Ox, Oy lần lượt tại A; B. Tính khoảng cách AB?

A. 4

B. 4√2

C. 8

D. 6√2

Lời giải:

Cho x = 0 ⇒ y = 4 ta được điểm B(0;4) thuộc trục Oy.

Cho y = 0 ⇒ x = 4 ta được điểm A(4; 0) thuộc trục Ox.

Tam giác OAB vuông tại O có OA = 4 và OB = 4 nên:

Chọn đáp án B.

Câu 11: Cho hàm số y = (3 – 2m) x + m − 2. Xác định m để đồ thị hàm số cắt trục hoành tại điểm có tung độ y = −4

A. m = 1     

B. m = −1   

C. m = −2   

D. m = 2

Lời giải:

Đồ thị hàm số cắt trục tung tại điểm có tung độ y = −4 nên tọa độ giao điểm là (0; −4)

Thay x = 0; y = −4 vào y = (3 – 2m) x + m – 2 ta được

(3 – 2m).0 + m − 2 = −4 ⇔ m = −2

Vậy m = −2

Đáp án cần chọn là: C

Câu 12: Cho hàm số . Xác định m để đồ thị hàm số cắt trục hoành tại điểm có tung độ y = 3

A. m = 11   

B. m = −11 

C. m = −12 

D. m = 1

Lời giải:

Đồ thị hàm số cắt trục tung tại điểm có tung độ y = 3 nên tọa độ giao điểm là (0; 3)

Thay x = 0; y = 3 vào  ta được

Vậy m = −11

Đáp án cần chọn là: B

Câu 13: Cho hàm số y = mx – 2 có đồ thị là đường thẳng d1 và cắt hàm số   có đồ thị là đường thẳng d2. Xác định m để hai đường thẳng d1 và d2 cắt nhau tại một điểm có hoành độ x = −4

Lời giải:

Ta có phương trình hoành độ giao điểm của d1 và d2: 

Để hai đường thẳng d1 và d2 cắt nhau tại một điểm có hoành độ x = −4 thì x = −4 thỏa mãn phương trình (*)

Đáp án cần chọn là: A

Câu 14: Cho hàm số  có đồ thị là đường thẳng d1 và hàm số y = 3x − 2 có đồ thị là đường thẳng d2. Xác định m để hai đường thẳng d1 và d2 cắt nhau tại một điểm có hoành độ x = −1

A. m = 3     

B. m = 12   

C. m = −12 

D. m = −3

Lời giải:

Ta có phương trình hoành độ giao điểm của d1 và d2:  

Để hai đường thẳng d1 và d2 cắt nhau tại một điểm có hoành độ x = −1 thì x = −1 thỏa mãn phương trình (*)

Đáp án cần chọn là: B

Câu 15: Cho hàm số y = (m + 1) x – 1 có đồ thị là đường thẳng d1 và hàm số y = x + 1 có đồ thị là đường thẳng d2. Xác định m để hai đường thẳng d1 và d2 cắt nhau tại một điểm có tung độ y = 4

Lời giải:

Thay y = 4 vào phương trình đường thẳng d2 ta được x + 1 = 4 ⇔ x = 3

Suy ra tọa độ giao điểm của d1 và d2 là (3; 4)

Thay x = 3; y = 4 vào phương trình đường thẳng d1 ta được:

Đáp án cần chọn là: C

II. Bài tập tự luận có lời giải

Câu 1:

Đồ thị hàm số y = 2x đi qua 2 điểm A(1; 2); O(0; 0).

Đồ thị hàm số y = 2x + 3 đi qua 2 điểm C(-1; 1); B(0; 3).

Nhận thấy đồ thị hàm số y = 2x song song với đồ thị hàm số y = 2x + 3.

Câu 2: Gọi A là giao điểm của hai đường thẳng y = x + 1 và y = 2x + 1, tìm tọa độ của điểm A?

Lời giải:

Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình:

x + 1 = 2x + 1 ⇒ x – 2x = 1 – 1

⇒ -x = 0 ⇒ x = 0

Với x = 0 thì y = 0 + 1 = 1

Suy ra, tọa độ điểm A(0; 1)

Câu 3: Vẽ đồ thị hàm số y = 3x – 1

Lời giải:

    + Bước 1: Cho x = 0 thì y = -1, ta được điểm P(0; -1) ∈ Oy.

         Cho y = 2 thì x = 1 ta được điểm Q(1; 2)

    + Bước 2: Vẽ đường thẳng đi qua hai điểm P và Q ta được đồ thị hàm số y = 3x – 1

III. Bài tập vận dụng

Câu 1: Cho đường thẳng d xác định bởi y = 2x + 11 . Đường thẳng d’ đối xứng với đường thẳng d qua trục hoành. Vậy phương trình đường thẳng d’ là?

Câu 2: Cho đường thẳng d có phương trình y = mx + m – 1 (m là tham số). Chứng minh rằng đường thẳng đã cho luôn đi qua một điểm cố định với mọi giá trị của m

B. Lý thuyết Đồ thị của hàm số y = ax + b

1. Đồ thị hàm số y = ax + b (a ≠ 0)

Đồ thị hàm số y = ax + b (a ≠ 0) là một đường thẳng:

– Cắt trục tung tại điểm có tung độ bằng b.

– Song song với đường thẳng y = ax nếu b ≠ 0; trùng với đường thẳng y = ax nếu b = 0

Chú ý. Đồ thị hàm số y = ax + b (a ≠ 0) còn được gọi là đường thẳng y = ax + b và b được gọi là tung độ gốc của đường thẳng.

Ví dụ 1. Gọi A là giao điểm của hai đường thẳng y = x − 1 và y = 3x + 1, tìm tọa độ của điểm A?

Lời giải:

Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình:

x − 1 = 3x + 1

$\iff$ 3x − x = − 1 − 1

$\iff$ 2x = − 2

$\iff$ x = − 1.

Với x = − 1 thì y = − 1 − 1 = − 2. Khi đó, A(− 1; − 2).

Vậy tọa độ giao điểm A(− 1; − 2).

2. Cách vẽ đồ thị hàm số y = ax + b (a ≠ 0)

• Khi b = 0 thì y = ax. Đồ thị hàm số y = ax là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm A(1; a).

• Xét trường hợp y = ax + b với a ≠ 0 và b ≠ 0.

Bước 1: Cho x = 0 thì y = b, ta được điểm P(0; b) thuộc trục tung Oy.

Cho y = 0 thì $x=\frac{-b}{a}$, ta được điểm $Q\left(-\frac{b}{a};0\right)$ thuộc trục hoành Ox.

Bước 2: Vẽ đường thẳng đi qua hai điểm P và Q ta được đồ thị hàm số y = ax + b (a ≠ 0).

 Chú ý: Vì đồ thị y = ax + b (a ≠ 0) là một đường thẳng nên muốn vẽ nó chỉ cần xác định hai điểm phân biệt thuộc đồ thị.

Ví dụ 2. Vẽ đồ thị hàm số y = 2x – 1.

Bước 1: Cho x = 0 thì y = −1, ta được điểm A(0; −1) ∈ Oy.

Cho y = 1 thì 2x – 1 = 1 $\iff$ x = 1, ta được điểm B(1; 1)

Bước 2: Vẽ đường thẳng đi qua hai điểm A và B, ta được đồ thị hàm số y = 2x – 1.

Ta có đồ thị hàm số: