Các dạng bài tập điển hình Liên hệ giữa cung và dây có lời giải

Tài liệu Bài tập Liên hệ giữa cung và dây gồm các nội dung chính sau:

I. Phương pháp giải

– tóm tắt lý thuyết ngắn gọn.

II. Bài tập

– gồm 6 bài tập vận dụng có đáp án và lời giải chi tiết giúp học sinh tự rèn luyện cách giải các dạng Bài tập Liên hệ giữa cung và dây.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

BÀI TẬP LIÊN HỆ GIỮA CUNG VÀ DÂY

I. Phương pháp giải

Sử dụng hai định lý sau:

Định lí 1:

Với hai cung nhỏ trong một đường tròn hay hai đường tròn bằng nhau :

a)     Hai cung bằng nhau căng hai dây bằng nhau

b)    Dây lớn hơn căng cung lớn hơn

Định lí 2:

Với hai cung nhỏ trong một đường tròn hay hai đường tròn bằng nhau

a)     Cung lớn hơn căng dây lớn hơn

b)    Dây lớn hơn căng cung lớn hơn

II. Bài tập

Bài 1: (10/71/SGK T2)

a)     Vẽ đường tròn tâm O bán kính $R=2cm$. Nêu cách vẽ cung AB có số đo bằng $60°$. Hỏi dây AB dài bao nhiêu cm

b)    Làm thế nào để chia được đường tròn thành sáu cung bằng nhau như hình vẽ b

Giải

a)     Cách vẽ cung AB có số đo bằng $60°$

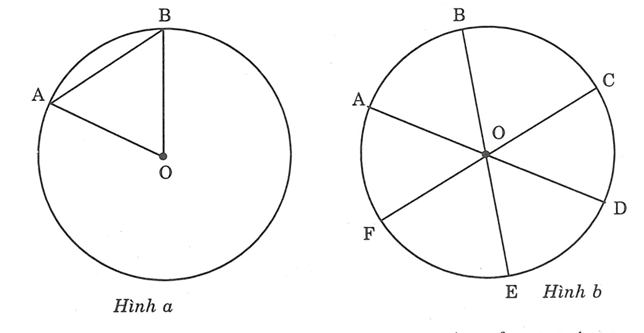
Vẽ đường tròn tâm O bán kính $R=2cm$. Lấy điểm A bất kỳ trên đường tròn này là tâm, vẽ đường tròn tâm A bán kính $AB=2cm$ cho cắt (O) tại B. Nối A và B với O ta được:

$\Delta AOB$ (vì đường tròn tâm A có bán kính $AB=2cm$ nên đi qua O) có $OA=AB=BO\Rightarrow \Delta AOB\text{ ®Òu}\Rightarrow \widehat{AOB}=60°\Rightarrow \text{s®}\stackrel{⏜}{AB}=60°$ (theo định lí : số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó)

b)    Cách chia đường tròn thành 6 cung bằng nhau

Vẽ đường tròn tâm O bán kính tùy ý. Trên đường tròn này lấy điểm A bất kỳ. Vẽ đường tròn tâm A bán kính bằng OA cho cắt (O) tại B.

Vẽ đường tròn tâm B bán kính OB cho cắt đường tròn (O) tại C. Vẽ các đường kính AD, BE, CF của đường tròn (O) ta được 6 cung $\stackrel{⏜}{AB}=\stackrel{⏜}{BC}=\stackrel{⏜}{CD}=\stackrel{⏜}{DE}=\stackrel{⏜}{EF}=\stackrel{⏜}{FA}$

Bài 2: (11/72/SGK T2)

Cho hai đường tròn bằng nhau (O) và $\left(O^{‘}\right)$ cắt nhau tại hai điểm A và B. Kẻ các đường kính AOC và $A{O}^{‘}D$. Gọi E là giao điểm thứ 2 của AC với đường tròn $\left(O^{‘}\right)$ khác điểm O

a)     So sánh các cung nhỏ BC và BD

b)    Chứng minh rằng B là điểm chính giữa cung EBD (tức là điểm B chia cung lớn ED thành hai cung bằng nhau $\stackrel{⏜}{BE}=\stackrel{⏜}{BD}$

Xem thêm