Bài tập Toán 9 Chương 1 Bài 7: Biến đổi đơn giản biểu thức chứa căn thức bậc hai (tiếp)
A. Bài tập Biến đổi đơn giản biểu thức chứa căn bậc hai (tiếp)
I. Bài tập trắc nghiệm
Câu 1: Rút gọn biểu thức với a > 0 ?
A. 3a B. a√3 C. 3√a D. a/√3
Lời giải:
Khử mẫu của biểu thức dưới dấu căn
Ta có:
Chọn đáp án C.
Câu 2: Rút gọn biểu thức
Lời giải:
Trục căn thức ở mẫu
Ta có:
Chọn đáp án C.
Câu 3: Cho biểu thức
Tìm giá trị của a để A – 1/A = 0?
A. a = 5 B. a = 3 C. a = 36 D. a = 25
Lời giải:
Ta có:
Ta có:
Chọn đáp án D.
Câu 4: Tính
A. 1
B. 0
C.√2
D.2√2
Lời giải:
Chọn đáp án B.
Câu 5: Tính
Lời giải:
Chọn đáp án C.
Câu 6: Tính
A. 0
B. 1
C. 2
D.3
Lời giải:
Chọn đáp án A.
Câu 7: Tìm x biết:
A. x = 2
B. x = 5
C. x = 10
D. x = 125
Lời giải:
Chọn đáp án B.
Câu 8: Rút gọn: (với x ≥ 0; y ≥ 0; x ≠ y )
Lời giải:
Với x ≥ 0; y ≥ 0; x ≠ y , áp dụng đưa thừa số ra ngoài dấu căn, ta có
Chọn đáp án A.
Câu 9: So sánh hai số 5√3 và 4√5
Lời giải:
Đáp án cần chọn là: D
II. Bài tập tự luận có lời giải
Câu 1: Cho biểu thức
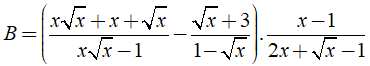 (với x ≥ 0; x ≠ 1 và x ≠ 1/4).
(với x ≥ 0; x ≠ 1 và x ≠ 1/4).
Tìm tất cả các giá trị của x để B < 0.
Lời giải:
Ta có:
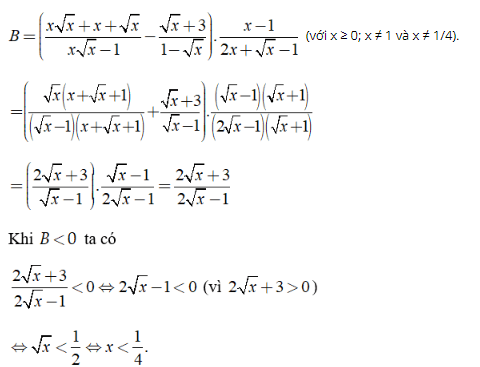
Kết hợp điều kiện ta có x ∈ [0; 1/4].
Câu 2: Giải các phương trình sau:
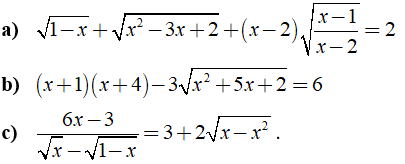
Lời giải:
a) Điều kiện xác định:
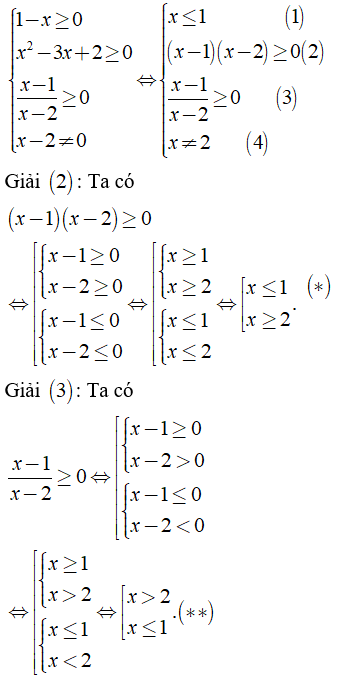
Kết hợp (1), (4), (*) và (**) ta có điều kiện xác định: x ≤ 1
Ta có
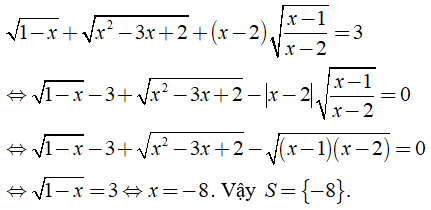
b) Điều kiện xác định: .
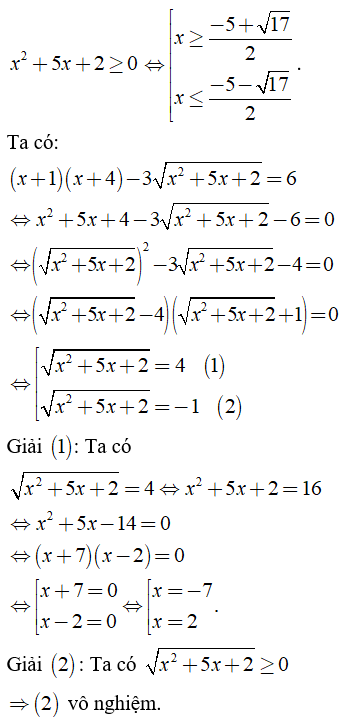
So sánh điều kiện ta có: x = -7; x = 2 (t/m). Vậy S = {-7; 2}.
c) Điều kiện xác định x ∈ [0; 1]\{1/2}.
Ta có:
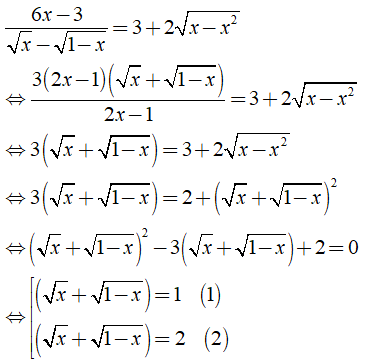
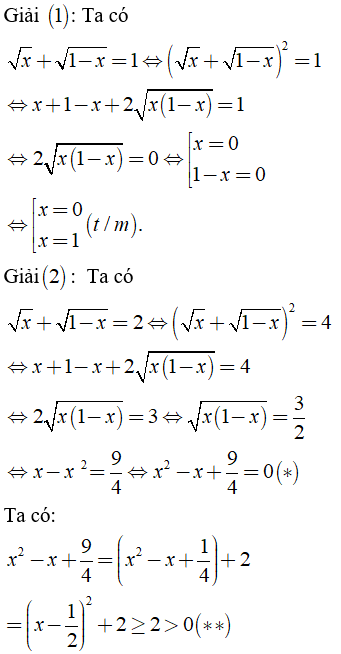
Từ (*) và (**) suy ra phương trình (2) vô nghiệm.
Vậy S = {0; 1}.
Câu 3: Rút gọn các biểu thức sau:
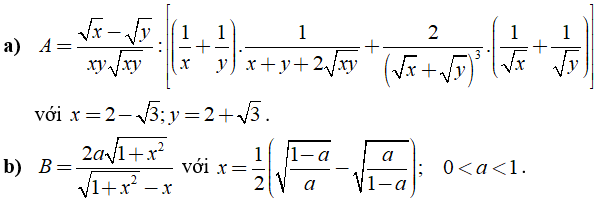
Lời giải:
a) Ta có:
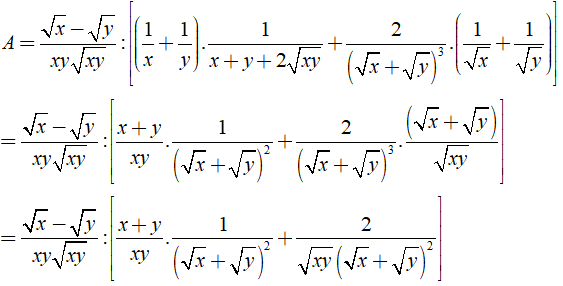
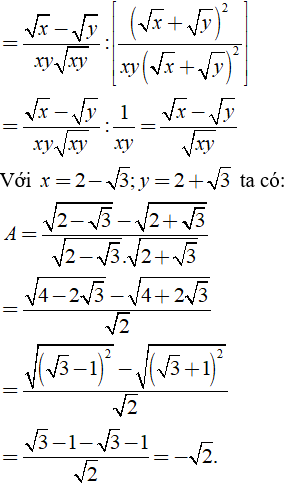
b) Ta có
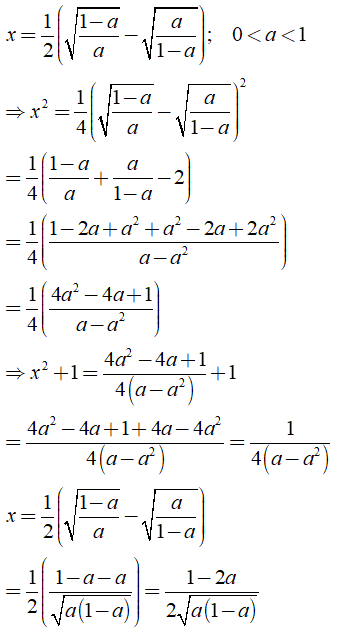
Khi đó: .
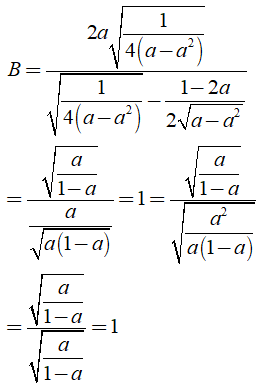
Câu 4: Chứng minh rằng
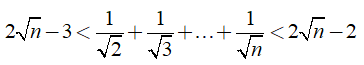 (n ∈ N; n ≥ 2)
(n ∈ N; n ≥ 2)
Lời giải:
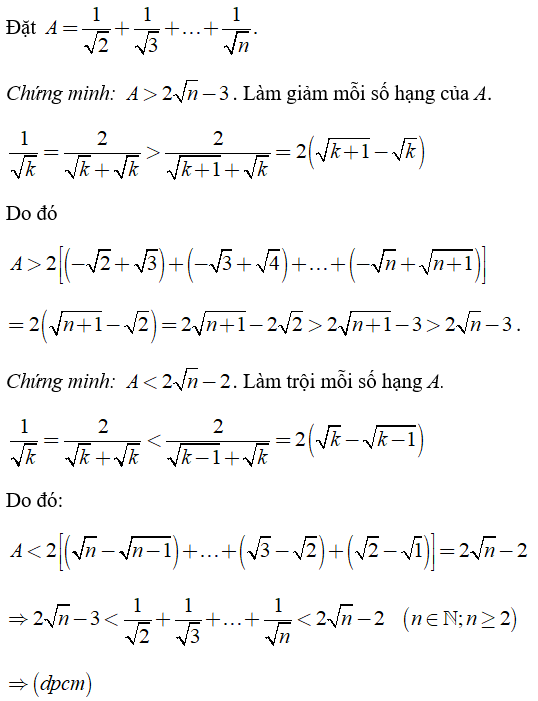
III. Bài tập vận dụng
Câu 1: Cho biểu thức
(với x ≥ 0; x ≠ 1 và x ≠ 1/4).
Tìm tất cả các giá trị của x để B < 0.
Câu 2: Giải các phương trình sau:
Câu 3: Rút gọn các biểu thức sau:
B. Lý thuyết Biến đổi đơn giản biểu thức chứa căn bậc hai (tiếp)
1.. Khử mẫu của biểu thức lấy căn
Tổng quát: Với các biểu thức A, B mà A. B ≥ 0 và B ≠ 0, ta có:
.
Ví dụ 4. Khử mẫu của biểu thức lấy căn
a) ;
b) với a > 0
Lời giải:
a)
b) Vì a > 0 nên 3a > 0. Do đó |3a| = 3a;
Vì a > 0 nên 9a3 > 0. Do đó |9a3| > 9a3.
Khi đó,
2.Trục căn thức ở mẫu
Trục căn thức ở mẫu số là biến đổi để biểu thức đó mất căn thức ở mẫu số.
Tổng quát:
• Với các biểu thức A, B mà B > 0 ta có:
.
• Với các biểu thức A, B, C mà A ≥ 0, A ≠ B2, ta có:
.
• Với các biểu thức A, B, C mà A ≥ 0, B ≥ 0, A ≠ B ta có:
.
Ví dụ 5. Trục căn thức ở mẫu
a) ;
b) .
Lời giải:
a)
b)