50 Bài tập Căn thức bậc hai và hằng đẳng thức (có đáp án) – Toán 9

Bài tập Toán 9 Chương 1 Bài 2: Căn thức bậc hai và hằng đẳng thức

A. Bài tập Căn thức bậc hai và hằng đẳng thức

I. Bài tập trắc nghiệm

Câu 1: Điều kiện xác định của biểu thức  là ?

A. x = 7/4.     

B. x ≥ 7/4.     

C. x ≤ 4/7.     

D. x > 4/7.

Lời giải:

 xác định ⇔ 7x – 4 ≥ 0 ⇔ x ≥ 4/7.

Chọn đáp án B.

Câu 2: Điều kiện xác định của biểu thức  là ?

A. x = 0.     B. x ≠ 2.     C. 0 < x < 2.     D. 0 ≤ x ≤ 2.

Lời giải:

 xác định

Chọn đáp án C.

Câu 3: Giá trị của biểu thức  là ?

A. S = 12.     B. S = 2.     C. S = √5.     D. S = 2√5

Lời giải:

Ta có

Chọn đáp án D.

Câu 4: Giá trị của phép toán  là?

A. 6.     B. 6√6.     C. 4√6.     D. 4.

Lời giải:

Ta có

Chọn đáp án B.

Câu 5: Phân tích biểu thức x2 – 2√3.x + 3 thành nhân tử ?

A. (x – √3)2.     B. (√x – 3)2.

C. (x + √3)2.     D. (x – √3)(x + √3).

Lời giải:

Ta có: x2 – 2√3.x + 3 = (x)2 – 2x(√3) + (√3)2 = (x – √3)2

Chọn đáp án A.

Câu 6: Rút ngọn biểu thức:  với a > 0

A. −9a            

B. −3a            

C. 3a                           

D. 9a

Lời giải:

Đáp án cần chọn là: C

Câu 7: Tìm x để  có nghĩa

Lời giải:

Đáp án cần chọn là: A

Câu 8: Tìm x để  có nghĩa

Lời giải:

Đáp án cần chọn là: A

Câu 9: Rút gọn biểu thức  với -4≤a≤4 ta được

A. 2a                          

B. 8                            

C. −8                          

D. −2a

Lời giải:

Đáp án cần chọn là: B

Câu 10: Rút gọn biểu thức  với  ta được:

A. −4a            

B. 4a                           

C. −6                          

D. 6

Lời giải:

Đáp án cần chọn là: D

Câu 11: Tìm x thỏa mãn phương trình 

A. x = 2                      

B. x = 4                      

C. x = 1                      

D. x = 3

Lời giải:

Đáp án cần chọn là: D

Câu 12: Tìm x thỏa mãn phương trình 

A. x = 2                      

B. x = 4                      

C. x = 1                      

D. x = 1; x = 2

Lời giải:

Đáp án cần chọn là: A

Câu 13: Nghiệm của phương trình  là:

A. x = 2                      

B. x = 5                      

C. x = 1                      

D. x = 3

Lời giải:

Đáp án cần chọn là: C

Câu 14: Nghiệm của phương trình 

A. x = 2                      

B. x = 5                      

C. x = 3                      

D. c = 3; x = 5

Lời giải:

Vậy phương trình có hai nghiệm là x = 3; x = 5

Đáp án cần chọn là: D

Câu 15: Nghiệm của phương trình  là

Lời giải:

Đáp án cần chọn là: C

II. Bài tập tự luận có lời giải

Câu 1: Rút gọn các biểu thức sau:

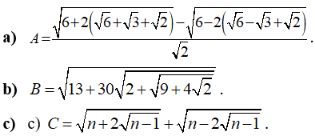
Lời giải:

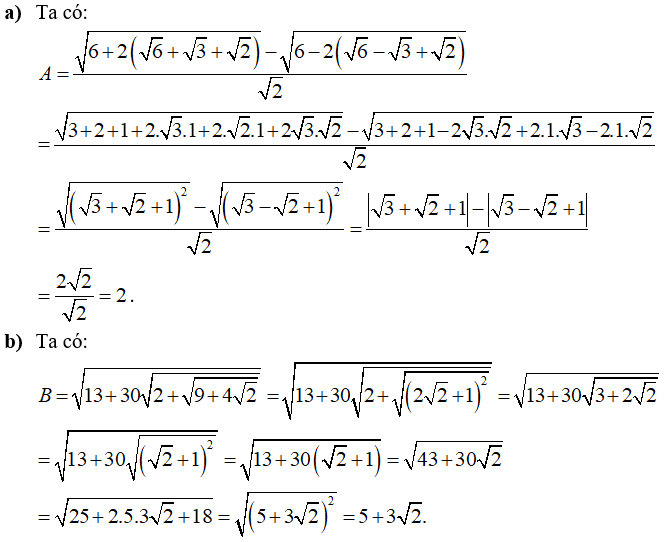
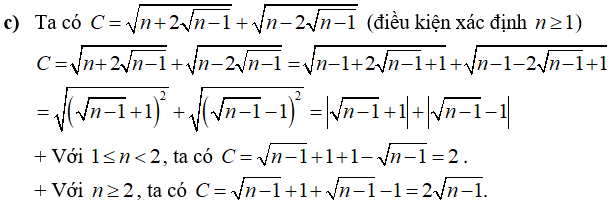
Câu 2: Giải các phương trình sau

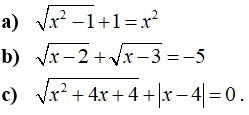
Lời giải:

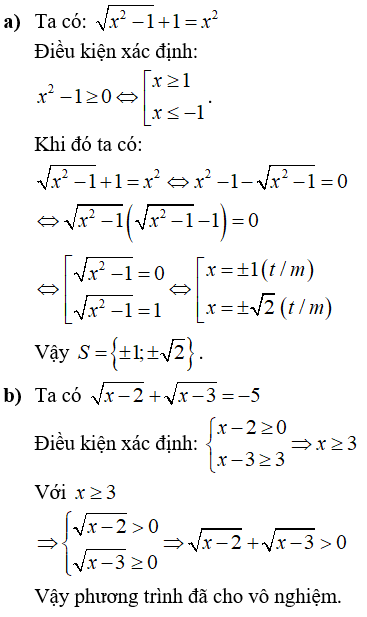
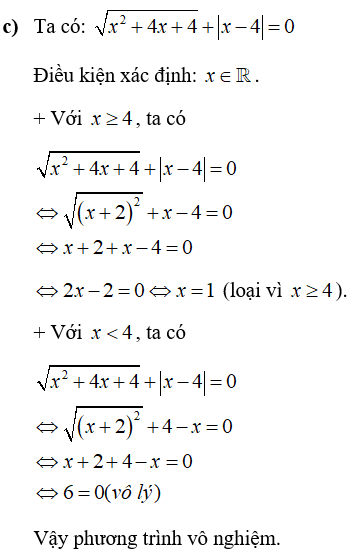
Câu 3: Cho biểu thức: 

a) Tìm tập xác định của biểu thức.

b) Rút gọn biểu thức A.

Lời giải:

a) Điều kiện xác định:

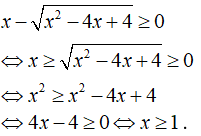
Vậy tập xác định là D = [1; +∞].

b) Ta có: .

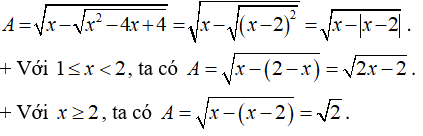
III. Bài tập vận dụng

Câu 1: Tính:

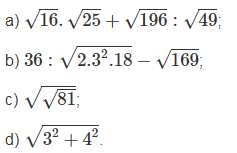
Câu 2: Tìm x để mỗi căn thức sau có nghĩa:

B. Lý thuyết Căn thức bậc hai và hằng đẳng thức

1. Căn thức bậc hai

Với A là một biểu thức đại số, người ta gọi $\sqrt{A}$ là căn thức bậc hai của A, còn A là biểu thức lấy căn hay còn gọi là biểu thức dưới dấu căn.

$\sqrt{A}$ xác định (có nghĩa) khi A lấy giá trị không âm.

Ví dụ 1. $\sqrt{5x}$ là căn thức bậc hai của 5x;

$\sqrt{5x}$ xác định khi 5x ≥ 0, tức là khi x ≥ 0.

2. Hằng đẳng thức $\sqrt{A^2}=\left|A\right|$

Định lí. Với mọi số a, ta có $\sqrt{a^2}=\left|a\right|$.

Ví dụ 2. Tính

a) $\sqrt{{14}^2}$;

b) $\sqrt{{(-20)}^2}$.

Lời giải:

a) $\sqrt{{14}^2}=\left|14\right|=14$.

b) $\sqrt{{(-20)}^2}=\left|-20\right|=20$.

Chú ý. Một cách tổng quát, với A là một biểu thức ta có $\sqrt{A^2}=\left|A\right|$, có nghĩa là:

$\sqrt{A^2}=A$ nếu A ≥ 0 (tức là A lấy giá trị không âm);

$\sqrt{A^2}=-A$ nếu A < 0 (tức là A lấy giá trị âm).

Ví dụ 3. Rút gọn

a) $\sqrt{{(x-4)}^2}$ với x < 4;

b) $\sqrt{a^6}$ với a ≥ 0.

Lời giải:

a) $\sqrt{{(x-4)}^2}=\left|x-4\right|=4-x$ (vì x < 4);

b) $\sqrt{a^6}=\sqrt{{\left(a^3\right)}^2}=\left|a^3\right|$.

Vì a ≥ 0 nên a³ ≥ 0, do đó | a³ | = a³.

Vậy $\sqrt{a^6}=a^3$ (với a ≥ 0).