Câu hỏi:
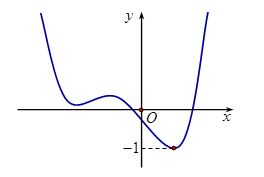
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Tìm số điểm cực trị của hàm số \(y = {2^{f\left( x \right)}} – {3^{f\left( x \right)}}\).
A. 6.
B. 5.
C. 4.
D. 3.
Đáp án chính xác
Trả lời:
Đáp án D
Xét hàm số \(g\left( x \right) = {2^{f\left( x \right)}} – {3^{f\left( x \right)}}\), với \(x \in \mathbb{R}\) ta có
\(g’\left( x \right) = f’\left( {x.} \right)\left[ {{2^{f\left( x \right)}}.\ln 2 – {3^{f\left( x \right)}}.\ln 3} \right]\)
\(g’\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f’\left( x \right) = 0\\{2^{f\left( x \right)}}.\ln 2 – {3^{f\left( x \right)}}.\ln 3 = 0\end{array} \right. \Rightarrow \left[ \begin{array}{l}f’\left( x \right) = 0\\{\left( {\frac{3}{2}} \right)^{f\left( x \right)}} = \frac{{\ln 2}}{{\ln 3}} = {\log _3}2\end{array} \right.\)
Từ đồ thị hàm số \(y = f\left( x \right)\) ta thấy \(f\left( x \right) \ge – 1,\forall x \in \mathbb{R}.\)
\( \Rightarrow {\left( {\frac{3}{2}} \right)^{f\left( x \right)}} \ge {\left( {\frac{3}{2}} \right)^{ – 1}} = \frac{2}{3} > {\log _3}2\) nên \(g’\left( x \right) = 0 \Leftrightarrow f’\left( x \right) = 0.\)
Số điểm cực trị của hàm số \(g\left( x \right)\) bằng số điểm cực trị của hàm số \(f\left( x \right).\)
Vậy hàm số \(y = {2^{f\left( x \right)}} – {3^{f\left( x \right)}}\) có đúng 3 điểm cực trị.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho a là số thực dương tùy ý và \(a \ne 1.\) Mệnh đề nào dưới đây là đúng?
Câu hỏi:
Cho a là số thực dương tùy ý và \(a \ne 1.\) Mệnh đề nào dưới đây là đúng?
A. \({\log _{\sqrt a }}{a^2} = 2.\)
B. \({\log _{\sqrt a }}{a^2} = 4.\)
Đáp án chính xác
C. \({\log _{\sqrt a }}{a^2} = a.\)
D. \({\log _{\sqrt a }}{a^2} = 2a.\)
Trả lời:
Đáp án B
Ta có \({\log _{\sqrt a }}{a^2} = {\log _{{a^{\frac{1}{2}}}}}{a^2} = \frac{2}{{\frac{1}{2}}}{\log _a}a = 4.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 3,{\rm{ }}{u_6} = \frac{3}{{32}}.\) Tìm q.
Câu hỏi:
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 3,{\rm{ }}{u_6} = \frac{3}{{32}}.\) Tìm q.
A. \(q = 2.\)
B. \(q = 4.\)
C. \(q = \frac{1}{4}.\)
D. \(q = \frac{1}{2}.\)
Đáp án chính xác
Trả lời:
Đáp án D
Ta có \({u_6} = {u_1}{q^5} \Rightarrow \frac{3}{{32}} = 3{q^5} \Rightarrow q = \frac{1}{2}.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Điểm M như hình vẽ bên là điểm biểu diễn số phức nào dưới đây?
Câu hỏi:
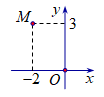
Điểm M như hình vẽ bên là điểm biểu diễn số phức nào dưới đây?
A. \(z = 3 – 2i.\)
B. \(z = – 2 + 3i.\)
Đáp án chính xác
C. \(z = 2 – 3i.\)
D. \(z = 3 + 2i.\)
Trả lời:
Đáp án B
Ta có \(M\left( { – 2;3} \right) \Rightarrow z = – 2 + 3i.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho \(\int\limits_0^{\frac{\pi }{2}} {f\left( x \right)dx} = 5.\) Tích phân \(\int\limits_0^{\frac{\pi }{2}} {\left[ {\cos x + f\left( x \right)} \right]dx} \) bằng
Câu hỏi:
Cho \(\int\limits_0^{\frac{\pi }{2}} {f\left( x \right)dx} = 5.\) Tích phân \(\int\limits_0^{\frac{\pi }{2}} {\left[ {\cos x + f\left( x \right)} \right]dx} \) bằng
A. 4.
B. 8.
C. 6.
Đáp án chính xác
D. 7.
Trả lời:
Đáp án C
Ta có \(\int\limits_0^{\frac{\pi }{2}} {\left[ {\cos x + f\left( x \right)} \right]dx} = \int\limits_0^{\frac{\pi }{2}} {\cos xdx + \int\limits_0^{\frac{\pi }{2}} {f\left( x \right)dx} = \sin x\left| {_{\scriptstyle\atop\scriptstyle0}^{\frac{\pi }{2}}} \right. + 5 = 6.} \)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian Oxyz, cho vectơ \(\vec a = 2\vec i + \vec k – 3\vec j.\) Tọa độ của vectơ \(\vec a\) là
Câu hỏi:
Trong không gian Oxyz, cho vectơ \(\vec a = 2\vec i + \vec k – 3\vec j.\) Tọa độ của vectơ \(\vec a\) là
A. \(\left( {1;{\mkern 1mu} 2;{\mkern 1mu} – 3} \right).\)
B. \(\left( {2;{\mkern 1mu} – 3;{\mkern 1mu} 1} \right).\)
Đáp án chính xác
C. \(\left( {2;{\mkern 1mu} 1;{\mkern 1mu} – 3} \right).\)
D. \(\left( {1;{\mkern 1mu} – 3;{\mkern 1mu} 2} \right).\)
Trả lời:
Đáp án B
Ta có \(\overrightarrow a = 2\overrightarrow i + \overrightarrow k – 3\overrightarrow j = 2\overrightarrow i – 3\overrightarrow j + \overrightarrow k \Rightarrow \overrightarrow a = \left( {2; – 3;1} \right).\)====== **** mời các bạn xem câu tiếp bên dưới **** =====