Tìm m để đồ thị hàm số y=x4-2m2x2+1 có ba cực trị tạo thành tam giác vuông cân

Câu hỏi:

Tìm m để đồ thị hàm số $y=x^4–2m^2{x}^2+1$ có ba cực trị tạo thành tam giác vuông cân

A. m = ± 1   

Đáp án chính xác

B. m = ± 2     

C. m = 3    

D. Đáp án khác

Trả lời:

Chọn A

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Tìm m để y=x3-3×2+mx-1 có hai điểm cực trị tại x1, x2 thỏa mãn x12+ x22=3
   
   

   Câu hỏi:
   

   Tìm m để $y=x^3–3x^2+mx–1$ có hai điểm cực trị tại $x_1, x_2$ thỏa mãn ${x_1}^2+ {x_2}^2=3$

   A. $m=\frac{3}{2}$

   Đáp án chính xác

   B. $m=1$

   C. $m=–2$

   D. $m=\frac{1}{2}$

   Trả lời:

   Chọn A
   $y‘=3x^2–6x+m.$
   Hàm số có hai cực trị khi y’ = 0 có hai nghiệm phân biệt :
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Tìm m để hàm số y=13×3-x2-mx+1 luôn đồng biến trên từng khoảng xác định của nó
   
   

   Câu hỏi:
   

   Tìm m để hàm số $y=\left(\frac{1}{3}\right)x^3–x^2–mx+1$ luôn đồng biến trên từng khoảng xác định của nó

   A. m < – 1   

   B. m > -1    

   C. m ≤ -1    

   Đáp án chính xác

   D. m > -1

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Tìm m để phương trình |x3+3×2-9x+2|=m có 6 nghiệm phân biệt
   
   

   Câu hỏi:
   

   Tìm m để phương trình $|x^3+3x^2–9x+2|=m$ có 6 nghiệm phân biệt

   A. 0 < m < 3   

   Đáp án chính xác

   B. m = 3     

   C. 3 < m < 29   

   D. m > -3

   Trả lời:

   Vẽ đồ thị hàm số $y=x^3+3x^2–9x+2$ (C)
   Giữ phần đồ thị (C) phía trên trục Ox, lấy đối xứng phần đồ thị (C) dưới trục Ox qua trục Ox.
   Bỏ phần đồ thị dưới trục Ox ta được đồ thị $y=\left|x^3+3x^2–9x+2\right|$.
   
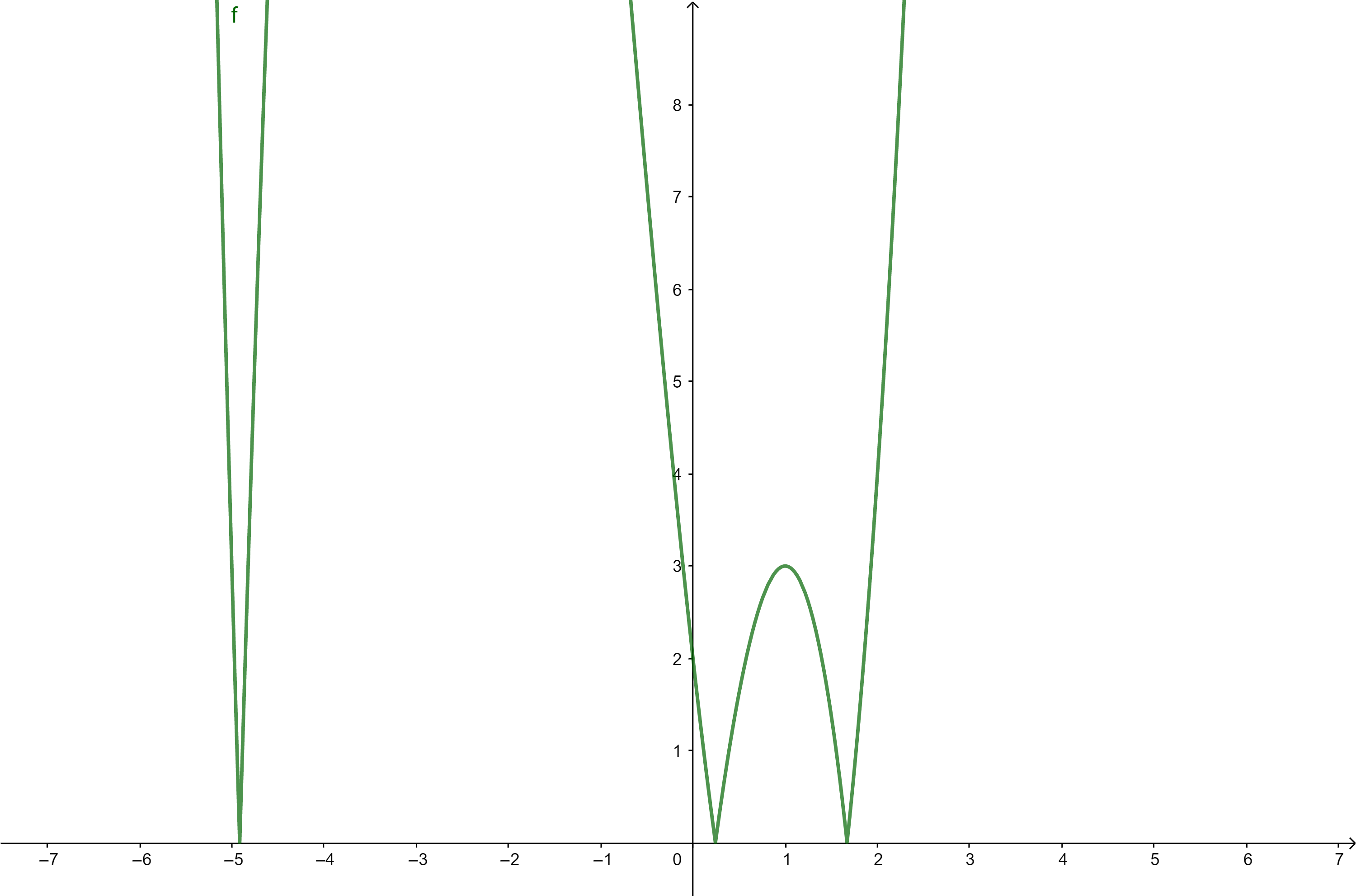
   Dựa vào đồ thị ta có đáp án A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Tìm m để hàm số y=-x3+(2m+1)x2-(m2-3m+2)x-4 có cực đại, cực tiểu nằm về hai phía so với trục tung
   
   

   Câu hỏi:
   

   Tìm m để hàm số $y=–x^3+(2m+1)x^2–(m^2–3m+2)x–4$ có cực đại, cực tiểu nằm về hai phía so với trục tung

   A. m ∈ (1; 2)    

   Đáp án chính xác

   B. m ∈ [1; 2]

   C. m ∈ (- ∞; 1) ∪ (2; +∞)

   D. m ∈ (- ∞; 1] ∪ [2; +∞)

   Trả lời:

   $y‘=–3x^2+2(2m+1)x–m^2+3m–2$Để hàm số đã cho có cực đại, cực tiểu nằm về hai phía so với trục tung khi và chỉ khi phương trình y’ = 0 có hai nghiệm $x_1, x_2$ trái dấu.Chọn A

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Tìm m để hàm số y=x3-3mx2+12x-2 nghịch biến trên khoảng (1; 4)
   
   

   Câu hỏi:
   

   Tìm m để hàm số $y=x^3–3m{x}^2+12x–2$ nghịch biến trên khoảng (1; 4)

   A. m ≥ 5/2   

   B. m ≤ 5/2   

   C. m ≤ 2    

   D. Đáp án khác

   Đáp án chính xác

   Trả lời:

   Chọn D

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====