Tập nghiệm của bất phương trình \({4^x} – {3.2^{x + 2}} + 32 \le 0\) là 

Câu hỏi:

Tập nghiệm của bất phương trình \({4^x} – {3.2^{x + 2}} + 32 \le 0\) là 

A.\(\left( {4;8} \right).\)

B.\(\left( {2;3} \right).\)

C.\(\left[ {2;3} \right].\)

Đáp án chính xác

D. \(\left[ {4;8} \right].\)

Trả lời:

Đáp án C.
Ta đặt \(t = {2^x};t >0.\) Thay vào bất phương trình đã cho ta thu được: \({t^2} – 12t + 32 \le 0 \Leftrightarrow 4 \le t \le 8.\)
Suy ra \(4 \le {2^x} \le 8 \Leftrightarrow 2 \le x \le 3.\) Tập nghiệm của bất phương trình đã cho là \(\left[ {2;3} \right].\)

====== **** mời các bạn xem câu tiếp bên dưới **** =====

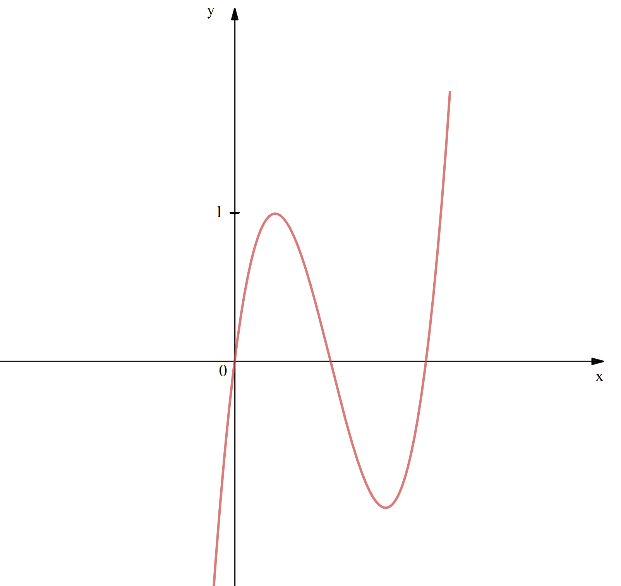
1. Cho hàm số \(f(x)\) có \(f(0) = 0\). Biết rằng \(y = f'(x)\) là hàm số bậc ba và có đồ thị là đường cong trong hình dưới đây, hàm số \(g(x) = f(f(x) – x)\) có bao nhiêu điểm cực trị ?
   
   

   Câu hỏi:
   

   Cho hàm số \(f(x)\) có \(f(0) = 0\). Biết rằng \(y = f'(x)\) là hàm số bậc ba và có đồ thị là đường cong trong hình dưới đây, hàm số \(g(x) = f(f(x) – x)\) có bao nhiêu điểm cực trị ?
   

   A.4.

   B.5.

   Đáp án chính xác

   C.6.

   D. 7.

   Trả lời:

   Đáp án B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hàm số \(f(x)\) có bảng biến thiên như sau: Giá trị cực tiểu của hàm số đã cho bằng
   
   

   Câu hỏi:
   

   Cho hàm số \(f(x)\) có bảng biến thiên như sau:
   
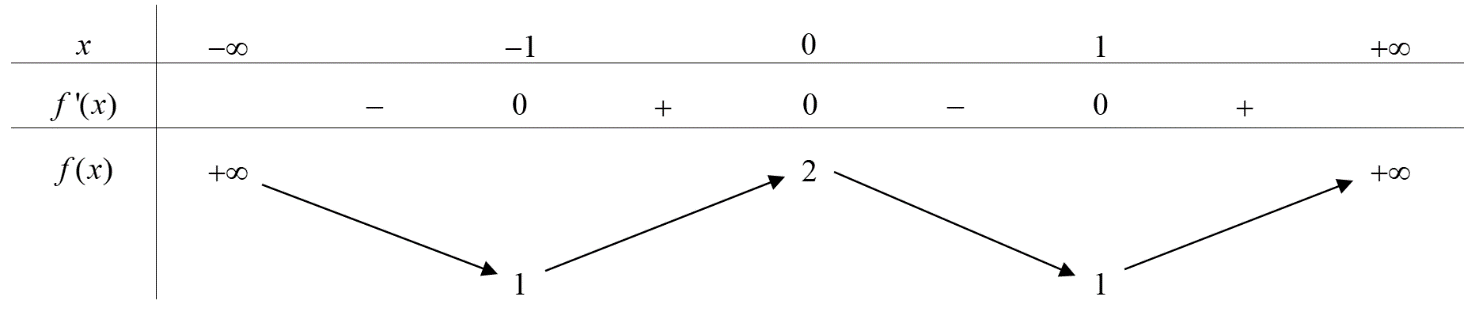
   Giá trị cực tiểu của hàm số đã cho bằng

   A. -1.

   B.0.

   C.1.

   Đáp án chính xác

   D. 2.

   Trả lời:

   Đáp án C.
   Nhìn vào bảng biến thiên ta dễ thấy cực tiểu của hàm số là 1.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Tập nghiệm của bất phương trình \({\log _5}x \ge 2\) là 
   
   

   Câu hỏi:
   

   Tập nghiệm của bất phương trình \({\log _5}x \ge 2\) là 

   A.\(\left( {25; + \infty } \right).\)

   Đáp án chính xác

   B.\(\left( {0;25} \right].\)

   C.\(\left( {25; + \infty } \right).\)

   D. \(\left[ {32; + \infty } \right).\)

   Trả lời:

   Đáp án A.
   Ta có \({\log _5}x \ge 2 \Leftrightarrow x \ge {5^2} \Leftrightarrow x \ge 25.\)
   Tập nghiệm của bất phương trình trên là \(S = \left[ {25; + \infty } \right).\)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Giá trị lớn nhất của hàm số \(f\left( x \right) = \cos x\) bằng
   
   

   Câu hỏi:
   

   Giá trị lớn nhất của hàm số \(f\left( x \right) = \cos x\) bằng

   A.\( – 1.\)

   B. 0.

   C. 2.

   D. 1.

   Đáp án chính xác

   Trả lời:

   Đáp án D.
   Ta có \( – 1 \le \cos x \le 1,\forall x \in \mathbb{R} \Rightarrow \mathop {Max}\limits_\mathbb{R} f\left( x \right) = 1.\)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Giá trị nhỏ nhất của hàm số \(f\left( x \right) = {x^3} – 36x\) trên đoạn \(\left[ {2;20} \right]\) bằng 
   
   

   Câu hỏi:
   

   Giá trị nhỏ nhất của hàm số \(f\left( x \right) = {x^3} – 36x\) trên đoạn \(\left[ {2;20} \right]\) bằng 

   A.\(48\sqrt 3 .\)

   B.\( – 50\sqrt 3 .\)

   C.\( – 81.\)

   D. \( – 48\sqrt 3 .\)

   Đáp án chính xác

   Trả lời:

   Đáp án D.
   Ta có \(f’\left( x \right) = 3{x^2} – 36.\) Xét \(f’\left( x \right) = 0 \Leftrightarrow 3{x^2} – 36 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\sqrt 3 \in \left[ {2;20} \right]\\x = – 2\sqrt 3 \notin \left[ {2;20} \right]\end{array} \right..\)
   Mà \(f\left( 2 \right) = – 64,f\left( {2\sqrt 3 } \right) = – 48\sqrt 3 ,f\left( {20} \right) = 7280.\)
   Vậy \(\mathop {\min }\limits_{x \in \left[ {2;20} \right]} f\left( x \right) = f\left( {2\sqrt 3 } \right) = – 48\sqrt 3 .\)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====