Câu hỏi:
Số giao điểm của đồ thị \(y = {x^3} – 2{x^2} + 3x – 2\) và trục hoành là
A. 1.
Đáp án chính xác
B. 3.
C. 0.
D. 2.
Trả lời:
Đáp án A.
Phương trình hoành độ giao điểm của \(y = {x^3} – 2{x^2} + 3x – 2\) với trục hoành là
\({x^3} – 2{x^2} + 3x – 2 = 0 \Leftrightarrow \left( {x – 1} \right)\left( {{x^2} – x + 2} \right) = 0 \Leftrightarrow x = 1\) (do \({x^2} – x + 2 >0,\forall x \in \mathbb{R}).\)
Vậy số giao điểm cần tìm là 1.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Xét các số thực dương \(a\) và \(b\) thỏa mãn \({\log _5}\left( {{5^a}{{.25}^b}} \right) = {5^{{{\log }_5}a + {{\log }_5}b + 1}}.\) Mệnh đề nào dưới đây đúng?
Câu hỏi:
Xét các số thực dương \(a\) và \(b\) thỏa mãn \({\log _5}\left( {{5^a}{{.25}^b}} \right) = {5^{{{\log }_5}a + {{\log }_5}b + 1}}.\) Mệnh đề nào dưới đây đúng?
A.\(a + 2b = ab.\)
B.\(a + 2b = 5ab.\)
Đáp án chính xác
C.\(2ab – 1 = a + b.\)
D. \(a + 2b = 2ab.\)
Trả lời:
Đáp án B.
Ta có \({\log _5}\left( {{5^a}{{25}^b}} \right) = {5^{{{\log }_5}a + {{\log }_5}b + 1}}\)
\( \Leftrightarrow {\log _5}{5^a} + {\log _5}{25^b} = {5^{{{\log }_5}a}}{.5^{{{\log }_5}b}}.5\)
\( \Leftrightarrow a + b{\log _5}25 = a.b.5\)
\( \Leftrightarrow a + 2b = 5ab\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình nón có góc ở đỉnh bằng \({60^0},\) bán kính đáy bằng \(a.\) Diện tích xung quanh của hình nón bằng
Câu hỏi:
Cho hình nón có góc ở đỉnh bằng \({60^0},\) bán kính đáy bằng \(a.\) Diện tích xung quanh của hình nón bằng
A.\(4\pi {a^2}.\)
B.\(\pi {a^2}\sqrt 3 .\)
C.\(2\pi {a^2}.\)
Đáp án chính xác
D. \(\pi {a^2}.\)
Trả lời:
Đáp án C.
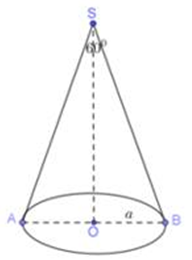
Ta có: \(SB = \frac{{OB}}{{\sin \widehat {BSO}}} = \frac{a}{{\frac{1}{2}}} = 2a\)
\({S_{xq}} = \pi Rl = \pi .a.2a = 2{a^2}\pi .\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) có đồ thị như hình vẽ
Khẳng định nào sau đây đúng?
Câu hỏi:
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) có đồ thị như hình vẽ
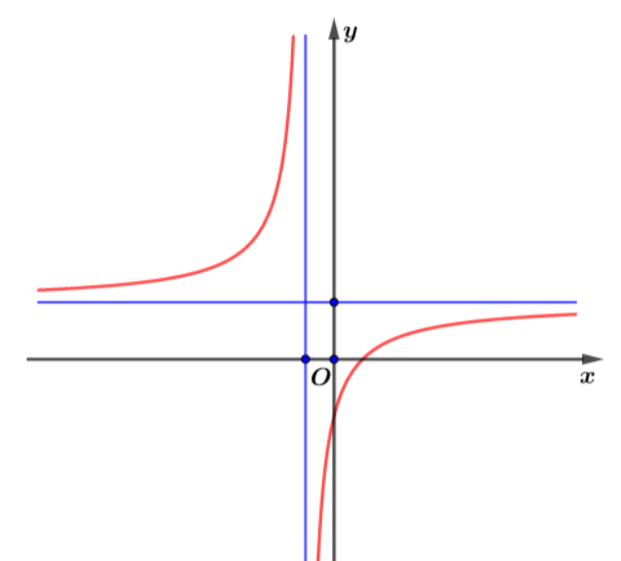
Khẳng định nào sau đây đúng?A.\(ab < 0;ad >0.\)
Đáp án chính xác
B.\(ad >0;bd >0.\)
C.\(bd < 0;bc >0.\)
D. \(ab < 0;ac < 0.\)
Trả lời:
Đáp án A.
Từ đồ thị của hàm số ta suy ra:
Tiệm cận đứng \(x = – \frac{d}{c} < 0 \Rightarrow cd >0\left( 1 \right)\)</>
Tiệm cận ngang \(y = \frac{a}{c} >0 \Rightarrow ac >0\left( 2 \right)\)
Từ \(\left( 1 \right),\left( 2 \right)\) suy ra \(ad >0.\)
Giao điểm với trục hoành \(x = – \frac{b}{a} >0 \Rightarrow ab < 0.\)
Vậy ta có \(ab < 0\) và \(ad >0.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Khối chóp tứ giác \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(6a,\) tam giác \(SAB\) đều và nằm trong mặt phẳng vuông góc với đáy có thể tích bằng
Câu hỏi:
Khối chóp tứ giác \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(6a,\) tam giác \(SAB\) đều và nằm trong mặt phẳng vuông góc với đáy có thể tích bằng
A.\(36\sqrt 3 {a^3}.\)
Đáp án chính xác
B.\(36{a^3}.\)
C.\(36\sqrt 2 {a^3}.\)
D. \(108\sqrt 3 {a^3}.\)
Trả lời:
Đáp án A.
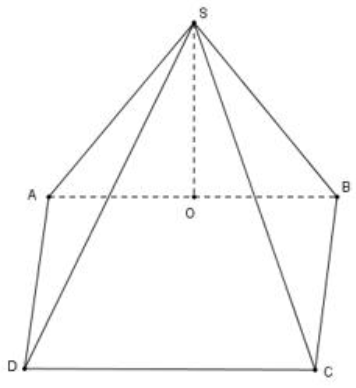
Vẽ đường cao
\(SO\) của tam giác đều \(SAB.\)
Ta có \(\left( {SAB} \right) \bot \left( {ABCD} \right) \Rightarrow SO \bot \left( {ABCD} \right).\)
Do đó \(SO\) là đường cao của hình nón \(S.ABCD\) và \(SO = \frac{{6a\sqrt 3 }}{2} = 3a\sqrt 3 .\)
Thể tích của khối chóp \(S.ABCD:V = \frac{1}{3}{S_{ABCD}}.SO = \frac{1}{3}.{\left( {6a} \right)^2}.3a\sqrt 3 = 36\sqrt 3 {a^3}.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Thiết diện qua trục của một hình nón là tam giác đều cạnh \(2a.\) Đường cao của hình nón là
Câu hỏi:
Thiết diện qua trục của một hình nón là tam giác đều cạnh \(2a.\) Đường cao của hình nón là
A.\(h = \frac{{a\sqrt 3 }}{2}.\)
B.\(h = a\sqrt 3 .\)
Đáp án chính xác
C.\(h = 2a.\)
D. \(h = a.\)
Trả lời:
Đáp án B.
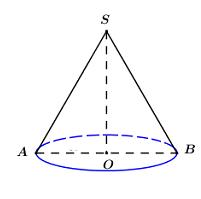
Ta có tam giác \(SAB\) là tam giác đều cạnh \(2a\) nên \(SA = SB = AB = 2a\)
Khi đó: \(R = OA = a,l = SA = 2a.\) Nên \(h = SO = a\sqrt 3 .\)
Vậy chọn đáp án B.====== **** mời các bạn xem câu tiếp bên dưới **** =====