Ông X muốn xây một bình chứa hình trụ có thể tích 72m3. Đáy làm bằng bêtông giá 100 nghìn đồng/m2, thành làm bằng tôn giá 90 nghìn đồng/m2, nắp bằng nhôm giá 140 nghìn đồng/m2. Vậy đáy của hình trụ có bán kính bằng bao nhiêu để chi phí xây dựng là thấp nhất?

Câu hỏi:

Ông X muốn xây một bình chứa hình trụ có thể tích $72m^3$. Đáy làm bằng bêtông giá 100 nghìn đồng/$m^2$, thành làm bằng tôn giá 90 nghìn đồng/$m^2$, nắp bằng nhôm giá 140 nghìn đồng/$m^2$. Vậy đáy của hình trụ có bán kính bằng bao nhiêu để chi phí xây dựng là thấp nhất?

A.$\frac{3\sqrt[3]{3}}{2\sqrt[3]{\pi }}\left(m\right)$

B.$\frac{3}{\sqrt[3]{\pi }}\left(m\right)$

Đáp án chính xác

C.$\frac{2}{\sqrt[3]{\pi }}\left(m\right)$

D.$\frac{\sqrt{3}}{\sqrt[3]{\pi }}\left(m\right)$

Trả lời:

Phương pháp giải:
– Gọi bán kính đáy và chiều cao của hình trụ lần lượt là $r,h\left(m\right)(r,h>0)$. Từ thể tích của hình trụ rút h theo r.
– Tính diện tích xung quanh và diện tích đáy, diện tích nắp của hình trụ.
– Dựa vào giá tiền từng bộ phận đề bài đã cho, tính tổng chi phí.
– Sử dụng BĐT Cô-si cho 3 số không âm a,b,c : $a+b+c\ge 3\sqrt[3]{abc}$. Dấu “=” xảy ra khi và chỉ khi a=b=c để tìm chi phí nhỏ nhất, từ đó tìm được r.
Giải chi tiết:
Gọi bán kính đáy và chiều cao của hình trụ lần lượt là $r,h\left(m\right)(r,h>0)$.
Vì thể tích hình trụ là $72m^3$nên ta có $\pi r^{2}h=72\iff h=\frac{72}{\pi r^2}$.
Diện tích thành (diện tích xung quanh) hình trụ là $2\pi rh=2\pi r.\frac{72}{\pi r^2}=\frac{144}{r}\left(m^2\right)$.
Diện tích đáy và nắp hình trụ là $\pi r^2\left(m^2\right)$.
Chi phí là: $90.\frac{144}{r}+100\pi r^2+140\pi r^2=240(\frac{54}{r}+\pi r^2)$(nghìn đồng).
Áp dụng BĐT Cô-si ta có: $\frac{54}{r}+\pi r^2=\frac{27}{r}+\frac{27}{r}+\pi r^2\ge 3\sqrt[3]{\frac{27}{r}+\frac{27}{r}+\pi r^2}=27\sqrt[3]{\pi }$.
Dấu “=” xảy ra $\iff \frac{27}{r}=\pi r^2\iff r^3=\frac{27}{\pi }\iff r=\frac{3}{\sqrt[3]{\pi }}\left(m\right)$.
Vậy chi phí thấp nhất đạt được khi bán kính đáy hình trụ là $\frac{3}{\sqrt[3]{\pi }}\left(m\right)$.
Đáp án B.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Thể tích khối cầu có bán kính r là:
   
   

   Câu hỏi:
   

   Thể tích khối cầu có bán kính $r$ là:

   A. $\frac{4}{3}\pi r^3$

   Đáp án chính xác

   B. $\frac{1}{3}\pi r^3$

   C. $\frac{4}{3}\pi r^2$

   D. $4\pi r^3$

   Trả lời:

   Phương pháp giải:
   Thể tích khối cầu có bán kính $r$ là $\frac{4}{3}\pi r^3$.
   Giải chi tiết:
   Thể tích khối cầu có bán kính $r$là $\frac{4}{3}\pi r^3$.
   Đáp án A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho dãy số \(\left( {{u_n}} \right)\) là cấp số nhân có số hạng đầu u1=1, công bội q=2. Tổng ba số hạng đầu của cấp số nhân là:
   
   

   Câu hỏi:
   

   Cho dãy số \(\left( {{u_n}} \right)\) là cấp số nhân có số hạng đầu $u_1=1$, công bội $q=2$. Tổng ba số hạng đầu của cấp số nhân là:

   A. 9

   B. 3

   C. 5

   D. 7

   Đáp án chính xác

   Trả lời:

   Phương pháp giải:
   Tổng n số hạng đầu tiên của CSN có số hạng đầu $u_1$, công bội q là $S_n=\frac{u_1(1-q^n)}{1-q}$.
   Giải chi tiết:
   Tổng ba số hạng đầu của cấp số nhân có $u_1=1$và $q=2$ là: $S_3=\frac{u_1(1-q^3)}{1-q}=\frac{1.(1-2^3)}{1-2}=7$
   Đáp án D

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây?
   
   

   Câu hỏi:
   

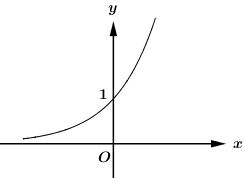
   Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây?
   

   A.$y={\log }_{3}x$

   B.$y={\log }_{\frac{1}{3}}x$

   C.$y=3^x$

   Đáp án chính xác

   D.$y={\left(\frac{1}{3}\right)}^x$

   Trả lời:

   Phương pháp giải:
   – Hàm số $y={\log }_{a}x(0<a\ne 1)$ có TXĐ $D=(0;+\infty )$.
   + Khi $a>1$, hàm số đồng biến trên D.
   + Khi 0 < a < 1, hàm số nghịch biến trên D.
   – Hàm số $y=a^x(0<a\ne 1)$ có TXĐ $D=(0;+\infty )$.
   + Khi $a>1$, hàm số đồng biến trên D.
   + Khi $0<a<1$, hàm số nghịch biến trên D.
   Giải chi tiết:
   Dựa vào đồ thị ta thấy hàm số đồng biến trên \(\mathbb{R}\) nên chỉ có đáp án C thỏa mãn, tức là hàm số $y=3^x$
   Đáp án C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Tìm tập nghiệm S của phương trình (20202021)4x=(20212020)2x−6.
   
   

   Câu hỏi:
   

   Tìm tập nghiệm S của phương trình ${\left(\frac{2020}{2021}\right)}^{4x}={\left(\frac{2021}{2020}\right)}^{2x-6}$.

   A.$S=\{-3\}$

   B.$S=\left\{3\right\}$

   C.$S=\{-1\}$

   D.$S=\left\{1\right\}$

   Đáp án chính xác

   Trả lời:

   Phương pháp giải:
   – Sử dụng công thức ${\left(\frac{1}{a}\right)}^m=a^{-m}$.
   – Giải phương trình mũ dạng $a^{f\left(x\right)}=a^{g\left(x\right)}\iff f\left(x\right)=g\left(x\right)$.
   Giải chi tiết:
   Ta có:
   ${\left(\frac{2020}{2021}\right)}^{4x}={\left(\frac{2021}{2020}\right)}^{2x-6}$
   $\iff {\left(\frac{2020}{2021}\right)}^{4x}={\left(\frac{2020}{2021}\right)}^{6-2x}$
   $\iff 4x=6-2x\iff 6x=6\iff x=1$
   Vậy tập nghiệm của phương trình là $S=\left\{1\right\}$.
   Đáp án D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Tìm tập hợp tất cả các giá trị của tham số m để hàm số y=1log3(x2−2x+3m)có tập xác định là \(\mathbb{R}\).
   
   

   Câu hỏi:
   

   Tìm tập hợp tất cả các giá trị của tham số m để hàm số $y=\frac{1}{\sqrt{{\log }_3(x^2-2x+3m)}}$có tập xác định là \(\mathbb{R}\).

   A.$[\frac{2}{3};10]$

   B.$(\frac{2}{3};+\infty )$

   Đáp án chính xác

   C.$[\frac{2}{3};+\infty )$

   D.$(-\infty ;\frac{2}{3})$

   Trả lời:

   Phương pháp giải:
   – Hàm căn thức xác định khi biểu thức trong căn không âm.
   – Hàm $y={\log }_{a}f\left(x\right)$xác định khi và chỉ khi $f\left(x\right)$ xác định và $f\left(x\right)>0$.
   Giải chi tiết:
   Hàm số $y=\frac{1}{\sqrt{{\log }_3(x^2-2x+3m)}}$có TXĐ là \(\mathbb{R}\) khi và chỉ khi:
   $\{\begin{array}{l}{\log }_3(x^2-2x+3m)>0\forall x\in ℝ\\ x^2-2x+3m>0\forall x\in ℝ\end{array}\iff \{\begin{array}{l}{x}^2-2x+3m>1\forall x\in ℝ\\ x^2-2x+3m>0\forall x\in ℝ\end{array}$
   $\iff x^2-2x+3m>1\forall x\in ℝ\iff x^2-2x-1>-3m\forall x\in ℝ(*)$
   Đặt $f\left(x\right)=x^2-2x-1$ ta có $f^{‘}\left(x\right)=2x-2=0\iff x=1$.
   BBT:
   
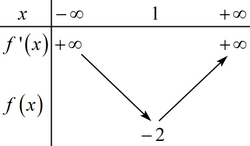
   Dựa vào BBT và từ (*) ta có $f\left(x\right)>-3m\forall x\in ℝ$$\iff -3m<\underset{ℝ}{min}f\left(x\right)=-2\iff m>\frac{2}{3}$.
   Vậy $m\in (\frac{2}{3};+\infty )$.
   Đáp án B

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====