Câu hỏi:
Nguyên hàm \(I = \int {{x^4}{e^{3x}}dx} \) là:
A. \(I = \left( {\frac{{{x^4}}}{3} – \frac{{4{x^3}}}{{{3^2}}} + \frac{{12{x^2}}}{{{3^3}}} – \frac{{24x}}{{{3^4}}} + \frac{{24}}{{{3^5}}}} \right){e^{3x}} + C\)
Đáp án chính xác
B. \(I = \frac{{{x^5}}}{5}.\frac{{{e^{3x}}}}{3} + C\)
C. \(I = \left( {\frac{{{x^4}}}{3} + \frac{{4{x^3}}}{{{3^2}}} – \frac{{12{x^2}}}{{{3^3}}} + \frac{{24x}}{{{3^4}}} – \frac{{24}}{{{3^5}}}} \right){e^{3x}} + C\)
D. \(I = \left( {\frac{{{x^4}}}{3} – \frac{{4{x^3}}}{{{3^2}}} + \frac{{12{x^2}}}{{{3^3}}}} \right){e^{3x}} + C\)
Trả lời:
Hướng dẫn giải
Nếu làm thông thường thì từng phần 4 lần ta mới thu được kết quả. Ở đây, chúng tôi trình bày theo sơ đồ đường chéo cho kết quả và nhanh chóng hơn.
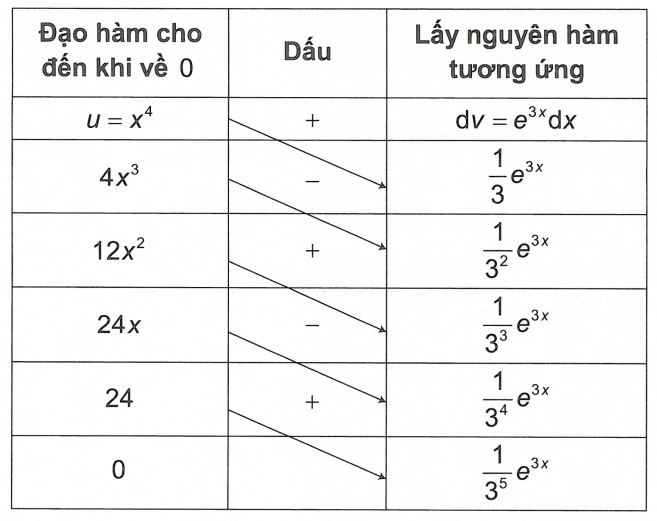
Vậy \(I = \left( {\frac{{{x^4}}}{3} – \frac{{4{x^3}}}{{{3^2}}} + \frac{{12{x^2}}}{{{3^3}}} – \frac{{24x}}{{{3^4}}} + \frac{{24}}{{{3^5}}}} \right){e^{3x}} + C\).
Chọn A.
====== **** mời các bạn xem câu tiếp bên dưới **** =====