Câu hỏi:
Kết quả nguyên hàm \(I = \int {{x^2}\sin 5xdx} \) là:
A. \( – \frac{1}{5}{x^2}\cos 5x – \frac{2}{{25}}x\sin 5x + \frac{2}{{125}}\cos 5x + C\)
B. \( – \frac{1}{5}{x^2}\cos 5x + \frac{2}{{25}}x\sin 5x – \frac{2}{{125}}\cos 5x + C\)
C. \(\frac{1}{5}{x^2}\cos 5x – \frac{2}{{25}}x\sin 5x + \frac{2}{{125}}\cos 5x + C\)
D. \( – \frac{1}{5}{x^2}\cos 5x + \frac{2}{{25}}x\sin 5x + \frac{2}{{125}}\cos 5x + C\)
Đáp án chính xác
Trả lời:
Hướng dẫn giải
Phân tích: Ở đây ta sẽ ưu tiên \(u = {x^2}\) là đa thức, tuy nhiên vì bậc của u là 2 nên ta sẽ từng phần hai lần mới thu được kết quả. Nhằm tiết kiệm thời gian, tôi gợi ý với phương pháp “sơ đồ đường chéo” cụ thể như sau:
Bước 1: Chia thành 3 cột:
+ Cột 1: Cột u luôn lấy đạo hàm đến 0.
+ Cột 2: Dùng để ghi rõ dấu của các phép toán đường chéo.
+ Cột 3: Cột dv luôn lấy nguyên hàm đến khi tương ứng với cột 1.
Bước 2: Nhân chéo kết quả của 2 cột với nhau. Dấu của phép nhân đầu tiên sẽ có dấu (+), sau đó đan dấu (-), (+), (-),… rồi cộng các tích lại với nhau.
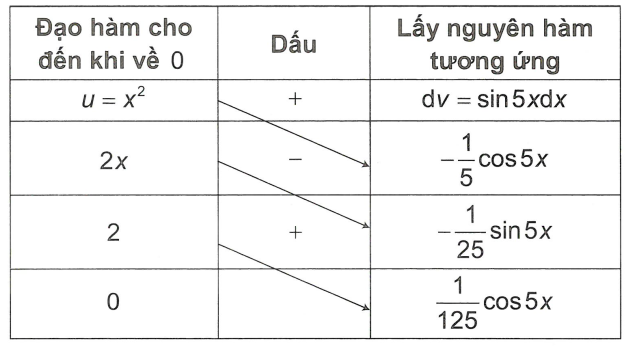
Khi đó \(I = – \frac{1}{5}{x^2}\cos 5x + \frac{2}{{25}}x\sin 5x + \frac{2}{{125}}\cos 5x + C\)
Chọn D.
====== **** mời các bạn xem câu tiếp bên dưới **** =====