Hàm số y = 3×2 – 2×3 đạt cực trị tại

Câu hỏi:

Hàm số y = 3x² – 2x³ đạt cực trị tại

A. x_CĐ = 0; x_CT = -1

B. x_CĐ = 1; x_CT = 0

Đáp án chính xác

C. x_CĐ = 0; x_CT = 1

D. x_CĐ = -1; x_CT = 0

Trả lời:

Đáp án B

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hàm số y =  1/3.x3 – 1/2.x2 – 12x – 1. Mệnh đề nào sau đây đúng ?
   
   

   Câu hỏi:
   

   Cho hàm số y =  1/3.x³ – 1/2.x² – 12x – 1. Mệnh đề nào sau đây đúng ?

   A. Hàm số đồng biến trên khoảng (4; +∞)

   Đáp án chính xác

   B. Hàm số nghịch biến trên khoảng (-3; +∞)

   C. Hàm số đồng biến trên khoảng (-∞; 4)

   D. Hàm số đồng biến trên khoảng (-3; 4)

   Trả lời:

   Đáp án A.
   y’ = x² – x – 12
   y’ > 0 <=> x² – x – 12 > 0 
   <=> x < -3 hoặc x > 4
   Vậy hàm số đồng biến trên (-∞ ; -3) và (4; +∞)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hàm số y = x4 – 2×2 – 3. Khẳng định nào sau đây là sai?
   
   

   Câu hỏi:
   

   Cho hàm số y = x⁴ – 2x² – 3. Khẳng định nào sau đây là sai?

   A. Hàm số nghịch biến trên khoảng (-∞; -1)

   B. Hàm số nghịch biến trên khoảng (0; 1)

   C. Hàm số nghịch biến trên khoảng (-1; 0)

   Đáp án chính xác

   D. Hàm số đồng biến trên khoảng (1; +∞)

   Trả lời:

   Đáp án C.
   TXĐ: D = R
   
   BXD
   
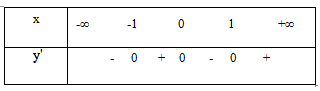
   Khẳng định C là sai

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Các khoảng nghịch biến của hàm số y = -1/4.×4 + 2×2 -5 là
   
   

   Câu hỏi:
   

   Các khoảng nghịch biến của hàm số y = -1/4.x⁴ + 2x² -5 là

   A. (-2; 0) và (2; +∞).

   Đáp án chính xác

   B. (-1; 0) và (1 ; +∞)

   C. (-∞; -2) và (0 ; 2).

   D. (-∞; -1) và (1; +∞)

   Trả lời:

   Đáp án A.
   Tập xác định D = R.
   y’ = -x³ + 4x.
   y’ = 0 ⇔ -x³ + 4x = 0 ⇔ x = 0 hoặc x = -2 hoặc x = 2
   Bảng biến thiên
   
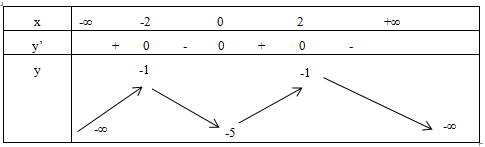
   Vậy hàm số nghịch biến trên (-2; 0) và (2; +∞).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Hàm số y = -x3 + 3x – 5 đồng biến trên khoảng nào sau đây?
   
   

   Câu hỏi:
   

   Hàm số y = -x³ + 3x – 5 đồng biến trên khoảng nào sau đây?

   A. (-1; 1).

   Đáp án chính xác

   B. (-∞; -1).

   C. (1; +∞).

   D. (-∞; 1).

   Trả lời:

   Đáp án A.
   Tập xác định D = R.
   y’ = -3x² + 3
   y’ = 0 ⇔ -3x² + 3 = 0 ⇔ x = 1 hoặc x = -1.
   Bảng biến thiên:
   
   Từ bảng biến thiên ta thấy hàm số đồng biến trên (-1; 1)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Hàm số y = x3 – 3×2 + 2 đồng biến trên khoảng nào trong các khoảng cho dưới đây
   
   

   Câu hỏi:
   

   Hàm số y = x³ – 3x² + 2 đồng biến trên khoảng nào trong các khoảng cho dưới đây

   A. (0; 2)

   B. (-∞; 2).

   C. (2; +∞).

   Đáp án chính xác

   D. R

   Trả lời:

   Đáp án C.
   Tập xác định: D = R
   Ta có y’ = 3x² – 6x; y’ = 0 
   
   Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====