Đặt log23= a và log35= b. Hãy biểu diễn log245 theo a và b

Câu hỏi:

Đặt log₂3= a và log₃5= b. Hãy biểu diễn log₂45 theo a và b

A. 2a+ 2ab

B.a+ ab

C. 3a+ ab

D.2a+ ab

Đáp án chính xác

Trả lời:

Ta có; log₂45= log₂( 3². 5) = 2log₂3+ log₂5
                    = 2a+ log₂3.log₃5= 2a+ ab
 
Do đó, log₂45= 2a+ ab.
Chọn D.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Với giá trị nào của x thì biểu thức A = log12x-13+x xác định?
   
   

   Câu hỏi:
   

   Với giá trị nào của x thì biểu thức $A = {\log }_{\frac{1}{2}}\frac{x–1}{3+x}$ xác định?

   A.-3≤ x≤ 1.

   B. 

   Đáp án chính xác

   C.

   D. .-3< x < 1.

   Trả lời:

   Biểu thức có nghĩa khi
   
   Chọn B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Với giá trị nào của x thì biểu thức: f( x) = log6( 2x- x2)  xác định?
   
   

   Câu hỏi:
   

   Với giá trị nào của x thì biểu thức: f( x) = log₆( 2x- x²)  xác định?

   A.0<x< 2.

   Đáp án chính xác

   B. x> 2.

   C.-1< x< 1.

   D.x< 3.

   Trả lời:

   Biểu thức có nghĩa khi  2x- x²> 0 hay 0< x< 2
   Chọn A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Với giá trị nào của x thì biểu thức:  f(x) = log5( x3-x2-2x) xác định?
   
   

   Câu hỏi:
   

   Với giá trị nào của x thì biểu thức:  f(x) = log₅( x³-x²-2x) xác định?

   A. 0<x < 1.

   B x> 1

   C. 

   Đáp án chính xác

   D.

   Trả lời:

   Biểu thức có nghĩa khi:  x³– x²-2x> 0 hay x( x²-x-2) > 0
   Cách 1: Ta có bảng xét dấu sau: 
   
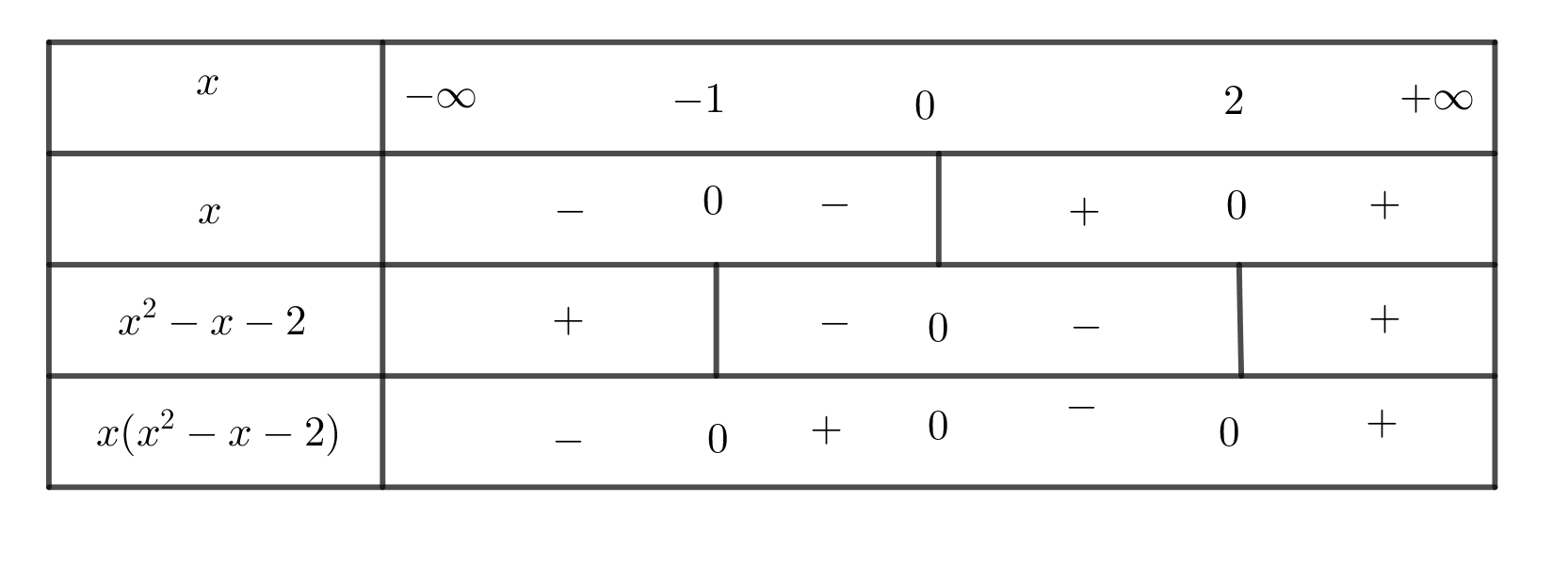
   Suy ra:  -1 < x < 0 hoặc x > 2
   Vậy để biểu thức có nghĩa thì $x\in \left(–1;0\right)\cup \left(2;+\infty \right)$
   Cách 2: sử dụng máy tính giải bất phương trình bậc 3.
   Chọn C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Điều kiện xác định của biểu thức  T = log(x2-4)(x2-6x+9)  là
   
   

   Câu hỏi:
   

   Điều kiện xác định của biểu thức  $T = log\sqrt{(x^2–4)(x^2–6x+9)}$  là

   A. 

   B. x>3

   C. 

   D. 

   Đáp án chính xác

   Trả lời:

   + Biểu thức có nghĩa khi ( x²– 4)( x²-6x+ 9) >0
   Hay ( x²-4) ( x-3)² > 0
   Ta có bảng xét dấu sau:
   
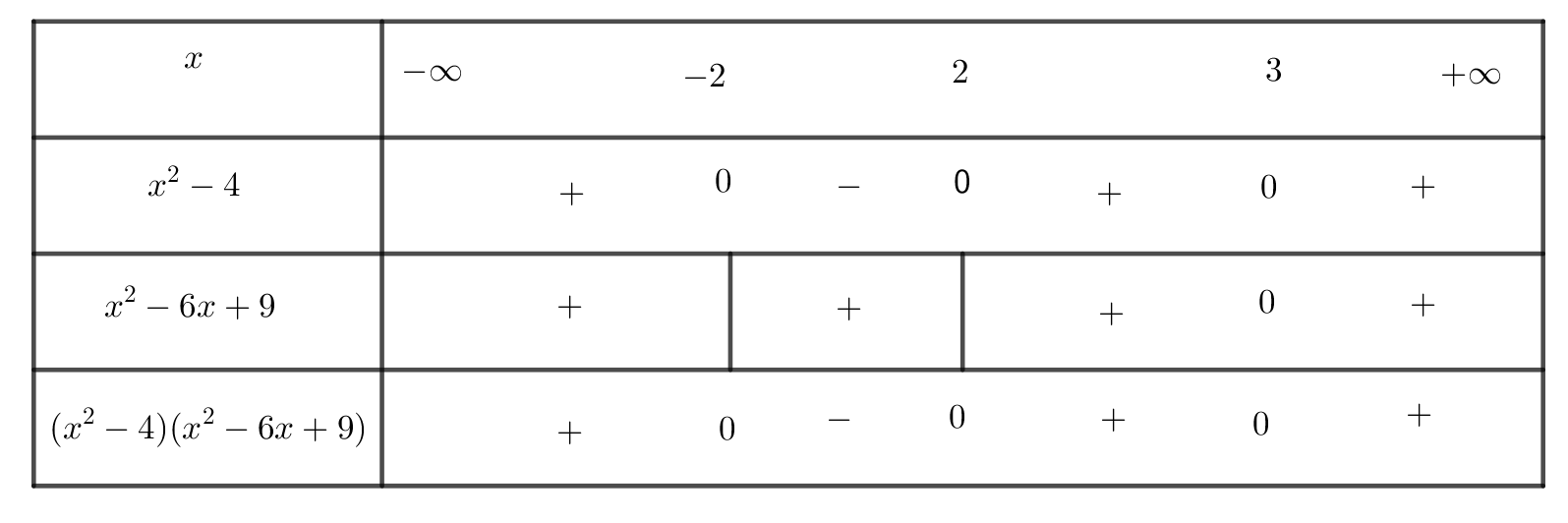
   Suy ra biểu thức có nghĩa khi $x\in \left(–\infty ;–2\right)\cup \left(2;3\right)\cup \left(3;+\infty \right)$
   Chọn D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho log2x = 2log2a23 + 3log21b2b(a;b&gt;0)Khi đó:
   
   

   Câu hỏi:
   

   Cho ${\log }_{2}x = 2{\log }_2\sqrt[3]{a^2} + 3{\log }_2\frac{1}{b^2\sqrt{b}}(a;b>0)$Khi đó:

   A. 

   B. 

   Đáp án chính xác

   C. 

   D. x= ab

   Trả lời:

   Ta có:
    ${\log }_{2}x = 2{\log }_2\sqrt[3]{a^2} + 3{\log }_2\frac{1}{b^2\sqrt{b}}(a;b>0), x>0\iff {\log }_{2}x={\log }_2{a}^{\frac{4}{3}}+{\log }_2{b}^{–\frac{15}{2}}\iff {\log }_{2}x={\log }_2{a}^{\frac{4}{3}}.b^{–\frac{15}{2}}\iff {\log }_{2}x={\log }_2{a}^{\frac{4}{3}}.b^{–\frac{15}{2}}\iff x = a^{\frac{4}{3}}.b^{–\frac{15}{2}}$
   Do đó $x=a^{\frac{4}{3}}.b^{\frac{–15}{2}}$
   Chọn B
    
    

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====