Cho tứ diện ABCD có AD⊥(ABC), ABC  có tam giác vuông tại B. Biết BC=2a,AB=2a3,AD=6a . Quay tam giác ABC và AB (bao gồm cả điểm bên trong 2 tam giác) xung quanh đường thẳng AB ta được hai khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng:

Câu hỏi:

Cho tứ diện ABCD có $AD\perp \left(ABC\right),ABC$  có tam giác vuông tại B. Biết $BC=2a,AB=2a\sqrt{3},AD=6a$ . Quay tam giác ABC và AB (bao gồm cả điểm bên trong 2 tam giác) xung quanh đường thẳng AB ta được hai khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng:

A. $\frac{5\sqrt{3}\pi a^3}{2}.$

B. $\frac{3\sqrt{3}\pi a^3}{2}.$

Đáp án chính xác

C. $\frac{64\sqrt{3}\pi a^3}{2}.$

D. $\frac{4\sqrt{3}\pi a^3}{2}.$

Trả lời:

Đáp án B

Khối nón N1  được sinh bởi tam giác ABC khi quay quanh AB có chiều cao h1=AB và bán kính đáy R1=BC .
Khối nón N2 được sinh bởi khi quay quanh AB có chiều cao h2=AB và bán kính đáy R2=AD.
Do hai khối nón cùng có chiều cao AB nên hai đáy của hai khối nón nằm trong hai mặt phẳng song song.

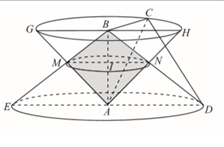
Trong mặt phẳng đáy của hình nón (N1)   kẻ đường kính GH//DE. Dễ dàng chứng minh được DEGH là hình thang cân.
Gọi $M=AG\cap BE;N=AH\cap BD;I=AB\cap MN$
Khi đó phần chung giữa hai khối nón (N1)  và (N2) là hai khối nón:
Khối nón (N3) đỉnh B, đường cao BI, bán kính đáy $IN\Rightarrow V_3=\frac{1}{3}\pi .I{N}^2.BI$
Khối nón (N4) đỉnh A, đường cao AI, bán kính đáy $IN\Rightarrow V_4=\frac{1}{3}\pi .I{N}^2.AI$
Thể tích phần chung $V=V_3+V_4=\frac{1}{3}\pi .I{N}^2.BI+\frac{1}{3}\pi .I{N}^2.AI=\frac{1}{3}\pi .I{N}^2.(AI+BI)=\frac{1}{3}\pi .I{N}^2.AB$

Áp dụng định lí Ta-let ta có: $\frac{MN}{GH}=\frac{AI}{AB};\frac{MN}{DE}=\frac{BI}{AB}\Rightarrow \frac{MN}{GH}+\frac{MN}{DE}=\frac{AI+BI}{AB}=1$
$\Rightarrow MN(\frac{1}{2BC}+\frac{1}{2AD})=1\iff MN.(\frac{1}{2.2a}+\frac{1}{2.6a})=1\iff MN=3a$

Dễ thấy I là trung điểm của $MN\Rightarrow IN=\frac{MN}{2}=\frac{3a}{2}$
Vậy $V=\frac{1}{3}\pi .{\left(\frac{3a}{2}\right)}^2.2a\sqrt{3}=\frac{3\sqrt{3}\pi a^3}{2}$

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Hình hộp chữ nhật đứng đáy là hình thoi có bao nhiêu mặt phẳng đối xứng?
   
   

   Câu hỏi:
   

   Hình hộp chữ nhật đứng đáy là hình thoi có bao nhiêu mặt phẳng đối xứng?

   A. 2.

   B. 1.

   C. 3.

   Đáp án chính xác

   D. 4.

   Trả lời:

   Đáp án C
   Có 4 mặt phẳng đối xứng như trong hình vẽ dưới đây:
   

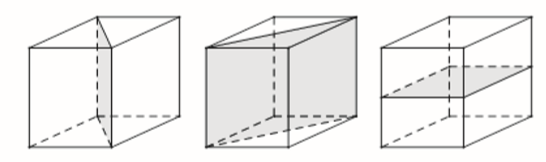
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho số phức z=(1−2i)2 . Tính mô đun của số phức  1z
   
   

   Câu hỏi:
   

   Cho số phức $z={(1-2i)}^2$ . Tính mô đun của số phức  $\frac{1}{z}$

   A.   $\frac{1}{5}.$

   Đáp án chính xác

   B.  $\sqrt{5}.$

   C.   $\frac{1}{25}.$

   D. $\frac{1}{\sqrt{5}}$

   Trả lời:

   Đáp án A
   Ta có: $\left|\frac{1}{z}\right|=\left|\frac{1}{{(1-2i)}^2}\right|=\frac{1}{{|1-2i|}^2}=\frac{1}{5}$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Tìm tất cả các giá trị của tham số m để phương trình x3+3×2−2=m   có hai nghiệm phân biệt.
   
   

   Câu hỏi:
   

   Tìm tất cả các giá trị của tham số m để phương trình $x^3+3x^2-2=m$   có hai nghiệm phân biệt.

   A.  $m\in (-\infty ;-2].$

   B.   $m\notin [-2;2].$

   C. $m\in [2;+\infty ).$

   D.   $m\in \{-2;2\}.$

   Đáp án chính xác

   Trả lời:

   Đáp án D
   Số nghiệm của phương trình $x^3+3x^2-2=m$   là số giao điểm của đồ thị hàm số  $y=x^3+3x^2-2$ và đường thẳng  $y=m$
   Ta có: $y‘=3x^2+6x=0\iff [\begin{array}{l}x=0\\ x=-2\end{array}$  . Ta có đồ thị hàm số như hình vẽ:
   Quan sát đồ thị hàm số ta có đường thẳng $y=m$   cắt đồ thị hàm số $y=x^3+3x^2-2$   tại 2 điểm phân biệt  $\iff [\begin{array}{l}m=2\\ m=-2\end{array}$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Trên đồ thị  (C):y=x+1x+2 có bao nhiêu điểm M mà tiếp tuyến với (C) tại M song song với đường thẳng   d:x+y=1.
   
   

   Câu hỏi:
   

   Trên đồ thị  $\left(C\right):y=\frac{x+1}{x+2}$ có bao nhiêu điểm M mà tiếp tuyến với (C) tại M song song với đường thẳng   $d:x+y=1.$

   A. 0.

   Đáp án chính xác

   B. 4.

   C. 3.

   D. 2.

   Trả lời:

   Đáp án A
   TXĐ: $D=R\backslash \left\{2\right\}.$  Ta có: $y‘=\frac{2.1-1.1}{{(x+2)}^2}=\frac{1}{{(x+2)}^2}$
   Gọi $M(x_o;\frac{x_o+1}{x_o+2})\in \left(C\right)$
   Ta có phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ $x=x_o$ là: $y‘=\frac{1}{{(x_o+2)}^2}(x-x_o)+\frac{x_o+1}{x_o+2}(d‘)$

   Để $(d‘)//\left(d\right):x+y=1\iff y=-x-1\Rightarrow \frac{1}{{(x_o+2)}^2}=-1$  (vô nghiệm)
    Không có điểm M nào thỏa mãn yêu cầu bài toán

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hàm số y=x3+bx2+cx+d,(b,c,d∈ℝ)  có đồ thị như hình vẽ. Mệnh đề nào dưới đây là đúng?
   
   

   Câu hỏi:
   

   Cho hàm số $y=x^3+b{x}^2+cx+d,(b,c,d\in ℝ)$  có đồ thị như hình vẽ. Mệnh đề nào dưới đây là đúng?
   

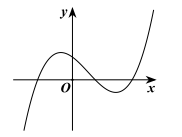
   A. $b<\mathrm{0,}c<\mathrm{0,}d>0.$

   Đáp án chính xác

   B.   $b>\mathrm{0,}c<\mathrm{0,}d>0.$

   C. $b<\mathrm{0,}c>\mathrm{0,}d<0.$

   D.   $b>\mathrm{0,}c>\mathrm{0,}d>0.$

   Trả lời:

   Đáp án A
   Với $x=0\Rightarrow d>0$
   Từ đồ thị ta thấy nếu gọi $x_1;x_2$ là hai điểm cực trị của hàm số thì khi đó
   $\{\begin{array}{l}{x}_1+x_2=\frac{-2b}{3a}>0\\ x_1{x}_2=\frac{c}{3a}<0\end{array}\Rightarrow \{\begin{array}{l}b<0\\ c<0\end{array}$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====