Câu hỏi:
Cho phương trình \(\left( {\sqrt x + \sqrt {x – 1} } \right)\left( {m\sqrt x + \frac{1}{{\sqrt {x – 1} }} + 16\sqrt[4]{{{x^2} – x}}} \right) = 1.\) Có bao nhiêu giá trị nguyên của tham số m để phương trình đã cho có đúng hai nghiệm thực phân biệt?
A. 11.
B. 9.
C. 20.
D. 4.
Đáp án chính xác
Trả lời:
Đáp án D
Điều kiện \(x > 1\). Phương trình \( \Leftrightarrow m\sqrt x + \frac{1}{{\sqrt {x – 1} }} + 16\sqrt[4]{{{x^2} – x}} = \sqrt x – \sqrt {x – 1} \)
\(\begin{array}{l} \Leftrightarrow m + \frac{1}{{\sqrt x .\sqrt {x – 1} }} + 16.\frac{{\sqrt[4]{{{x^2} – x}}}}{{\sqrt x }} = 1 – \frac{{\sqrt {x – 1} }}{{\sqrt x }}\\ \Leftrightarrow m = – 16.\sqrt[4]{{\frac{{{x^2} – x}}{{{x^2}}}}} – \frac{{x – 1}}{{\sqrt {x\left( {x – 1} \right)} }} – \frac{1}{{\sqrt {x\left( {x – 1} \right)} }} + 1 \Leftrightarrow m = – 16.\sqrt[4]{{\frac{{x – 1}}{x}}} – \sqrt {\frac{x}{{x – 1}}} + 1.\end{array}\)
Đặt \(t = \sqrt[4]{{\frac{{x – 1}}{x}}} \in \left( {0;1} \right)\), ta có \(m = – 16t – \frac{1}{{{t^2}}} + 1\).
Xét hàm số \(f\left( t \right) = – 16t – \frac{1}{{{t^2} + 1}}\), với \(t \in \left( {0;1} \right)\) ta có \(f’\left( t \right) = – 16 + \frac{2}{{{t^3}}} = 0 \Rightarrow t = \frac{1}{2}\).
Xét bảng sau:
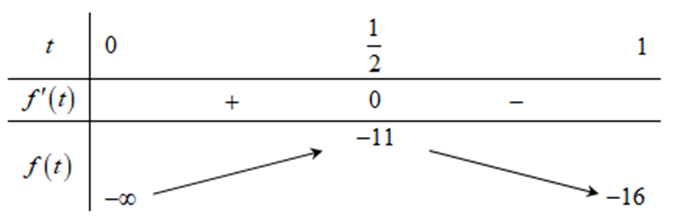
Từ đó ta được \( – 16 < m < – 11\). Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { – 15; – 14; – 13; – 12} \right\}\).
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 3,{\rm{ }}q = \frac{1}{2}.\) Tính \({u_5}.\)
Câu hỏi:
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 3,{\rm{ }}q = \frac{1}{2}.\) Tính \({u_5}.\)
A. \({u_5} = \frac{3}{{32}}.\)
B. \({u_5} = \frac{3}{{16}}.\)
Đáp án chính xác
C. \({u_5} = \frac{3}{{10}}.\)
D. \({u_5} = \frac{{15}}{2}.\)
Trả lời:
Đáp án B
Ta có \({u_5} = {u_1}{q^4} = \frac{3}{{16}}.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho a là số thực dương tùy ý và \(a \ne 1.\) Tính \(P = {\log _{\frac{a}{2}}}\frac{{{a^3}}}{8}.\)
Câu hỏi:
Cho a là số thực dương tùy ý và \(a \ne 1.\) Tính \(P = {\log _{\frac{a}{2}}}\frac{{{a^3}}}{8}.\)
A. \(P = \frac{1}{3}.\)
B. \(P = – \frac{1}{3}.\)
C. \(P = 3.\)
Đáp án chính xác
D. \(P = – 3.\)
Trả lời:
Đáp án C
Ta có \(P = {\log _{\frac{a}{2}}}\frac{{{a^3}}}{8} = {\log _{\frac{a}{2}}}{\left( {\frac{a}{2}} \right)^3} = 3\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Điểm M như hình vẽ bên là điểm biểu diễn số phức nào dưới đây?
Câu hỏi:
Điểm M như hình vẽ bên là điểm biểu diễn số phức nào dưới đây?
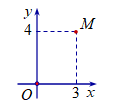
A. \(z = 4 + 3i.\)
B. \(z = 3 + 4i.\)
Đáp án chính xác
C. \(z = 4 – 3i.\)
D. \(z = 3 – 4i.\)
Trả lời:
Đáp án B
Ta có \(M\left( {3;4} \right) \Rightarrow z = 3 + 4i\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Câu hỏi:
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
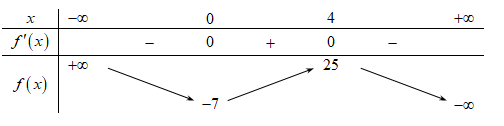
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?A. \(\left( {0;4} \right).\)
B. \(\left( { – \infty ;0} \right).\)
Đáp án chính xác
C. \(\left( { – 7; + \infty } \right).\)
D. \(\left( { – \infty ;25} \right).\)
Trả lời:
Đáp án B
Hàm số \(f\left( x \right)\) nghịch biến trên \(\left( { – \infty ;0} \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho \(\int\limits_0^{\frac{\pi }{2}} {f\left( x \right)dx} = 5.\) Tích phân \(\int\limits_0^{\frac{\pi }{2}} {\left[ {\sin x + f\left( x \right)} \right]dx} \) bằng
Câu hỏi:
Cho \(\int\limits_0^{\frac{\pi }{2}} {f\left( x \right)dx} = 5.\) Tích phân \(\int\limits_0^{\frac{\pi }{2}} {\left[ {\sin x + f\left( x \right)} \right]dx} \) bằng
A. 4.
B. 8.
C. 6.
Đáp án chính xác
D. 7.
Trả lời:
Đáp án C
Ta có \(\int\limits_0^{\frac{\pi }{2}} {\left[ {\sin x + f\left( x \right)} \right]dx} = \int\limits_0^{\frac{\pi }{2}} {\sin xdx} + \int\limits_0^{\frac{\pi }{2}} {f\left( x \right)dx} = – \cos \left| \begin{array}{l}^{\frac{\pi }{2}}\\_0\end{array} \right. + 5 = 6\).====== **** mời các bạn xem câu tiếp bên dưới **** =====