Câu hỏi:
Cho hình lăng trụ đứng \(ABC.A’B’C’\) có đáy là tam giác cân có \(AB = BC = 3a.\) Đường thẳng \(A’C\) tạo với đáy một góc \({60^0}.\) Trên cạnh \(A’C\) lấy điểm \(M\) sao cho \(A’M = 2MC.\) Biết rằng \(A’B = a\sqrt {31} .\) Khoảng cách từ \(M\) đến mặt phẳng \(\left( {ABB’A’} \right)\) là
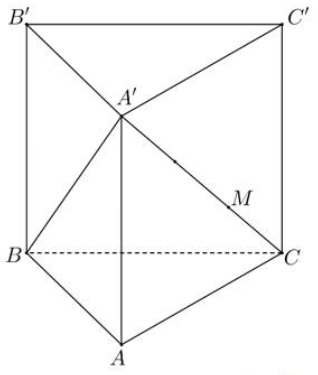
A.\(2a\sqrt 2 .\)
B. \(3a\sqrt 2 .\)
C.\(\frac{{4a\sqrt 2 }}{3}.\)
Đáp án chính xác
D. \(\frac{{3a\sqrt 2 }}{4}.\)
Trả lời:
Đáp án C.
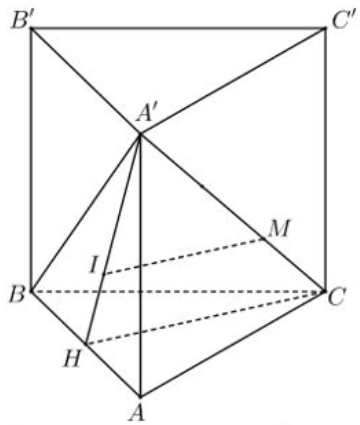
Hình lăng trụ đứng \(ABC.A’B’C’ \Rightarrow A\) là hình chiếu của \(A’\) trên mặt đáy \(\left( {ABC} \right)\)
\( \Rightarrow \widehat {A’CA} = \left( {\widehat {A’C,\left( {ABC} \right)}} \right) = \widehat {A’CA} = {60^0}\)
\(\Delta A’CA\) vuông tại \(A \Rightarrow A’A = AC.\tan \widehat {A’CA} = 3a.\tan {60^0} = 3a\sqrt 3 \)
\(\Delta A’AB\) vuông tại \(A \Rightarrow AB = \sqrt {A'{B^2} – A'{A^2}} = \sqrt {{{\left( {a\sqrt {31} } \right)}^2} – {{\left( {3a\sqrt 3 } \right)}^2}} = \sqrt {4{a^2}} = 2a\)
Kẻ \(CH \bot AB\) tại \(H \Rightarrow H\) là trung điểm của \(AB\) (do \(\Delta ABC\) cân tại \(C)\)
Mà \(A’A \bot \left( {ABC} \right) \Rightarrow A’A \bot CH \Rightarrow CH \bot \left( {ABB’A’} \right)\)
Kẻ \(MI//CH,I \in A’H \Rightarrow MI \bot \left( {ABB’A’} \right) \Rightarrow MI\) là khoảng cách từ \(M\) tới \(mp\left( {ABB’A’} \right)\)
Ta có: \(HA = \frac{{AB}}{2} = \frac{{2a}}{2} = a \Rightarrow CH = \sqrt {A{C^2} – H{A^2}} = \sqrt {{{\left( {3a} \right)}^2} – {a^2}} = \sqrt {8{a^2}} = 2a\sqrt 2 \)
\(MI//HC \Rightarrow \frac{{MI}}{{HC}} = \frac{{A’M}}{{AC}},\) mà \(A’M = 2MC \Rightarrow \frac{{A’M}}{{AC}} = \frac{2}{3} \Rightarrow \frac{{MI}}{{HC}} = \frac{2}{3}\)
\( \Rightarrow MI = \frac{2}{3}HC = \frac{2}{3}.2a\sqrt 2 = \frac{{4a\sqrt 2 }}{3}\)
Vậy khoảng cách từ \(M\) đến mặt phẳng \(\left( {ABB’A’} \right)\) là \(\frac{{4a\sqrt 2 }}{3}.\)
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Số đỉnh của một khối lăng trụ tam giác là
Câu hỏi:
Số đỉnh của một khối lăng trụ tam giác là
A.9.
B. 3.
C. 6.
Đáp án chính xác
D. 12.
Trả lời:
Đáp án C.
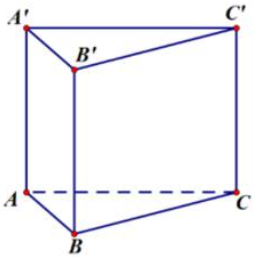
Khối lăng trụ tam giác có 6 đỉnh.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Đạo hàm của hàm số \(y = {x^4}\) là
Câu hỏi:
Đạo hàm của hàm số \(y = {x^4}\) là
A.\(y’ = 4{x^3}.\)
Đáp án chính xác
B.\(y’ = 0.\)
C.\(y’ = 4{x^2}.\)
D. \(y’ = 4x.\)
Trả lời:
Đáp án A.
Ta có: \(y’ = \left( {{x^4}} \right)’ = 4{x^3}.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên sau:
Khẳng định nào sau đây là khẳng định đúng?
Câu hỏi:
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên sau:
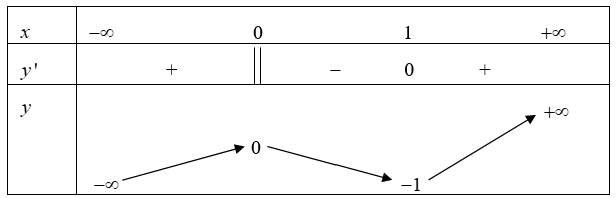
Khẳng định nào sau đây là khẳng định đúng?A. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng \( – 1.\)
B. Hàm số có đúng một cực trị.
C. Hàm số có giá trị cực tiểu bằng 1.
D. Hàm số đạt cực đại tại \(x = 0\) và đạt cực tiểu tại \(x = 1.\)
Đáp án chính xác
Trả lời:
Đáp án D.
Từ bảng biến thiên ta thấy, tính từ trái qua phải:
Dấu của \(y’\) đổi dấu từ (+) sang (-) khi qua \(x = 0,\) nên tại \(x = 0\) hàm số đạt cực đại.
Dấu của \(y’\) đổi dấu từ (-) sang (+) khi qua \(x = 1,\) nên tại \(x = 1\) hàm số đạt cực tiểu.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- \(\mathop {\lim }\limits_{x \to – 1} \left( {1 – x – {x^3}} \right)\) bằng
Câu hỏi:
\(\mathop {\lim }\limits_{x \to – 1} \left( {1 – x – {x^3}} \right)\) bằng
A.\( – 1.\)
B. 3.
Đáp án chính xác
C.\( – 3.\)
D. 1.
Trả lời:
Đáp án B.
Ta có: \(\mathop {\lim }\limits_{x \to – 1} \left( {1 – x – {x^3}} \right) = 1 – \left( { – 1} \right) – {\left( { – 1} \right)^3} = 3.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho khối lăng trụ có diện tích đáy \(B = 6\) và chiều cao \(h = 3.\) Thể tích của khối lăng trụ đã cho bằng
Câu hỏi:
Cho khối lăng trụ có diện tích đáy \(B = 6\) và chiều cao \(h = 3.\) Thể tích của khối lăng trụ đã cho bằng
A. 18.
Đáp án chính xác
B. 54.
C. 36.
D. 2.
Trả lời:
Đáp án A.
Thể tích khối lăng trụ là \(V = Bh = 6.3 = 18.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====