Câu hỏi:
Cho hình lăng trụ đứng \(ABC.A’B’C’\) có đáy \(ABC\) là tam giác vuông tại \(A,AB = a\sqrt 3 ,BC = 2a,\) đường thẳng \(AC’\) tạo với mặt phẳng \(\left( {BCC’B’} \right)\) một góc \({30^0}.\) Diện tích của mặt cầu ngoại tiếp hình lăng trụ đã cho bằng
A.\(24\pi {a^2}\).
B.\(3\pi {a^2}\).
C.\(4\pi {a^2}\).
D.\(6\pi {a^2}\).
Đáp án chính xác
Trả lời:
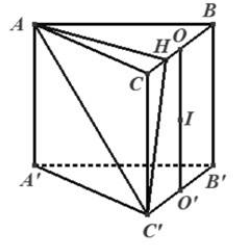
Ta có \(AC = \sqrt {B{C^2} – A{B^2}} = a\)
Gọi \(H\) là hình chiếu của \(A\) trên \(BC \Rightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{a\sqrt 3 }}{2}.\)
Ta có \(\left( {AC’,\left( {BCC’B’} \right)} \right) = \left( {AC’,HC’} \right) = \widehat {AC’H} \Rightarrow \widehat {AC’H} = {30^0} \Rightarrow AC’ = 2AH = a\sqrt 3 .\)
\( \Rightarrow CC’ = \sqrt {AC{‘^2} – A{C^2}} = a\sqrt 2 .\)
Gọi \(O,O’,I\) lần lượt là trung điểm của \(BC,B’C’,OO’ \Rightarrow I\) là tâm mặt cầu ngại tiếp lăng trụ.
\( \Rightarrow R = AI = \sqrt {A{O^2} + O{I^2}} = \sqrt {{{\left( {\frac{{BC}}{2}} \right)}^2} + {{\left( {\frac{{CC’}}{2}} \right)}^2}} = \frac{{a\sqrt 6 }}{2}.\)
Vậy diện tích mặt cầu là \(4.\pi .{\left( {\frac{{a\sqrt 6 }}{2}} \right)^2} = 6\pi {a^2}.\)
Đáp án D
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R},\) có \(f'\left( x \right) = {\left( {x + 2} \right)^2}{\left( {x – 2} \right)^3}\left( { – x + 5} \right).\) Số điểm cực trị của hàm số \(y = f\left( x \right)\) là
Câu hỏi:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R},\) có \(f’\left( x \right) = {\left( {x + 2} \right)^2}{\left( {x – 2} \right)^3}\left( { – x + 5} \right).\) Số điểm cực trị của hàm số \(y = f\left( x \right)\) là
A.0.
B.2.
Đáp án chính xác
C.1.
D.3.
Trả lời:
Ta có \(y’ = 0 \Leftrightarrow {\left( {x + 2} \right)^2}{\left( {x – 2} \right)^3}\left( { – x + 5} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = – 2\\x = 2\\x = 5\end{array} \right..\)
Bảng biến thiên của hàm số như sau
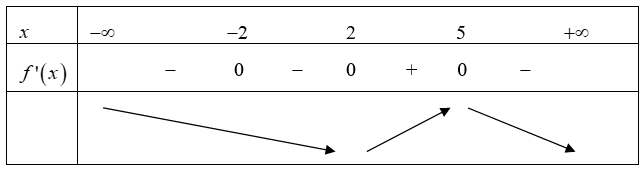
Vậy hàm số \(y = f\left( x \right)\) có 2 điểm cực trị.
Đáp án B====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
Hàm số nghịch biến trên khoảng nào dưới đây?
Câu hỏi:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
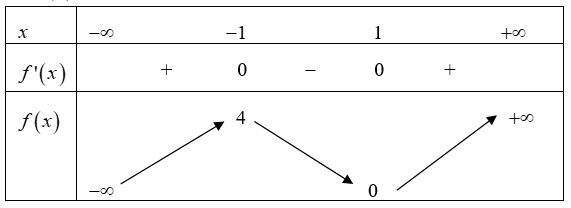
Hàm số nghịch biến trên khoảng nào dưới đây?A.\(\left( { – \infty ; – 1} \right).\)
B.\(\left( { – 1;1} \right).\)
Đáp án chính xác
C.\(\left( {0;2} \right).\)
D.\(\left( {0;4} \right).\)
Trả lời:
Từ bảng biến thiên ta có hàm số nghịch biến trên khoảng \(\left( { – 1;1} \right).\)
Đáp án B====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Hàm số nào sau đây nghịch biến trên từng khoảng xác định của nó?
Câu hỏi:
Hàm số nào sau đây nghịch biến trên từng khoảng xác định của nó?
A.\(y = \frac{{x + 5}}{{ – x – 1}}\).
B.\(y = \frac{{x – 1}}{{x + 1}}\).
C.\(y = \frac{{2x + 1}}{{x – 3}}\).
Đáp án chính xác
D.\(y = \frac{{x – 2}}{{2x – 1}}\).
Trả lời:
Xét hàm số \(y = \frac{{2x + 1}}{{x – 3}}.\)
Tập xác định \(D = \mathbb{R}\backslash \left\{ 3 \right\}.\)
Ta có \(y’ = \frac{{ – 7}}{{{{\left( {x – 3} \right)}^2}}} < 0,\forall x \in D.\)
Vậy hàm số trên nghịch biến trên từng khoảng xác định của nó.
Đáp án C====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R},\) có đạo hàm \(f'\left( x \right) = {x^3}{\left( {x – 1} \right)^2}\left( {x + 2} \right).\) Hỏi hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực trị?
Câu hỏi:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R},\) có đạo hàm \(f’\left( x \right) = {x^3}{\left( {x – 1} \right)^2}\left( {x + 2} \right).\) Hỏi hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực trị?
A.0.
B.2.
Đáp án chính xác
C.3.
D.1.
Trả lời:
Ta có \(f’\left( x \right) = 0 \Leftrightarrow {x^3}{\left( {x – 1} \right)^2}\left( {x + 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x = – 2\end{array} \right..\)
Bảng biến thiên
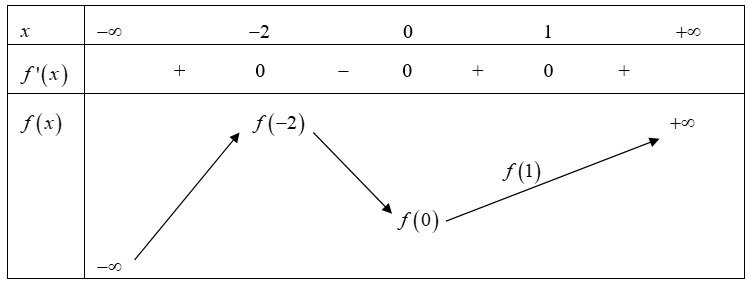
Vậy hàm số \(y = f\left( x \right)\) có 2 điểm cực trị.
Đáp án B====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tổng diện tích các mặt của một hình lập phương bằng 96. Tính thể tích của khối lập phương đó là?
Câu hỏi:
Tổng diện tích các mặt của một hình lập phương bằng 96. Tính thể tích của khối lập phương đó là?
A.84.
B.64.
Đáp án chính xác
C.48.
D.91.
Trả lời:
Gọi \(a\) là cạnh hình lập phương, ta có:
\({S_{tp}} = 6{a^2} = 96 \Leftrightarrow {a^2} = 16 \Leftrightarrow a = 4\)
Vậy thể tích của khối lập phương là \(V = {a^3} = {4^3} = 64\)
Đáp án B====== **** mời các bạn xem câu tiếp bên dưới **** =====