Câu hỏi:
Cho hình chóp SABCD có ABCD là hình chữ nhật cạnh vuông góc với mặt phẳng \(\left( {ABCD} \right)\) và SA=2. Gọi M,N,P lần lượt là chân đường cao hạ từ A lên các cạnh Thể tích khối chóp AMNP bằng
A.\(\frac{8}{{75}}.\)
Đáp án chính xác
B.
C.\(\frac{9}{{16}}.\)
D.
Trả lời:
Hướng dẫn gải:
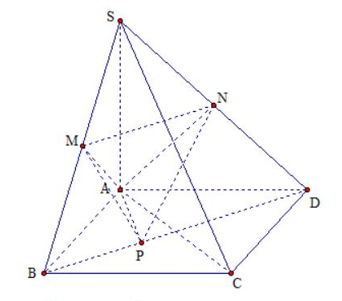
Ta có:
+) \(\frac{{BP}}{{BD}} = \frac{{A{B^2}}}{{B{D^2}}} = \frac{{A{B^2}}}{{A{B^2} + A{D^2}}} = \frac{1}{5} \Rightarrow BP = \frac{1}{5}BD,\) suy ra:
Tam giác SAD vuông cân tại A nên \(\frac{{SN}}{{SD}} = \frac{1}{2} \Rightarrow d\left( {N;\left( {ABCD} \right)} \right) = \frac{1}{2}SA = 1.\)
+)
Suy ra:
Vậy
Đáp án A
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng 2a, chiều cao cạnh bên bằng 3a.Tính thể tích V của khối chóp đã cho.
Câu hỏi:
Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng 2a, chiều cao cạnh bên bằng 3a.Tính thể tích V của khối chóp đã cho.
A.
B.
Đáp án chính xác
C.
D.\(V = \frac{{4{a^3}}}{3}.\)
Trả lời:
Chọn B.
* Diện tích đáy là:
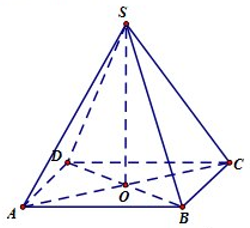
* Gọi là tâm của \(ABCD\) ta có thể tích V của khối chóp đã cho là:
là tâm của \(ABCD\) ta có thể tích V của khối chóp đã cho là: ====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hai số thực dương a và b. Biểu thức abbaab35 được viết dưới dạng lũy thừa với số mũ hữu tỉ là:
Câu hỏi:
Cho hai số thực dương a và b. Biểu thức được viết dưới dạng lũy thừa với số mũ hữu tỉ là:
A.\({x^{\frac{7}{{30}}}}.\)
B.
C.
D.
Đáp án chính xác
Trả lời:
Chọn D.
Ta có:====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Gọi M,m thứ tự là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \frac{{{x^2} + 3}}{{x – 1}}\) trên đoạn [-2;0] Tính P=M+m.
Câu hỏi:
Gọi M,m thứ tự là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \frac{{{x^2} + 3}}{{x – 1}}\) trên đoạn [-2;0] Tính P=M+m.
A.P=1
B.
C.\(P = – \frac{{13}}{3}.\)
D.
Đáp án chính xác
Trả lời:
Chọn D.
Ta có suy ra
Xét trên [-2;0] ta có và \(f\left( 0 \right) = – 3.\)
Vậy và , do đó====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tổng tất cả các giá trị nguyên của m để hàm số \(y = \frac{1}{3}{x^3} – \left( {m – 1} \right){x^2} + x – m\) đồng biến trên tập xác định bằng.
Câu hỏi:
Tổng tất cả các giá trị nguyên của m để hàm số \(y = \frac{1}{3}{x^3} – \left( {m – 1} \right){x^2} + x – m\) đồng biến trên tập xác định bằng.
A.3.
Đáp án chính xác
B.2.
C.4.
D. 1.
Trả lời:
Chọn A.
Tập xác định
Ta có để hàm số đồng biến với \(\forall x \in D\) thì mà nên Vậy đáp án là A.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tính thể tích của khối chóp có chiều cao h và diện tích đáy là \(B\) là
Câu hỏi:
Tính thể tích của khối chóp có chiều cao h và diện tích đáy là \(B\) là
A.
Đáp án chính xác
B.
C.
D.
Trả lời:
Chọn A.
Áp dụng công thức tính thể tích khối chóp ta chọn đáp án A.====== **** mời các bạn xem câu tiếp bên dưới **** =====