Câu hỏi:
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\) và \(AC = a.\) Biết tam giác \(SAB\) cân tại \(S\) và nằm trong mặt phẳng vuông góc với mặt phẳng đáy; góc giữa đường thẳng \(SD\) và mặt đáy bằng \(60^\circ .\) Khoảng cách giữa hai đường thẳng \(AD\) và \(SC\) bằng
\(\frac{{a\sqrt {609} }}{{19}}\).
B.\(\frac{{a\sqrt {609} }}{{29}}\).
Đáp án chính xác
C.\(\frac{{a\sqrt {600} }}{{29}}\).
D.\(\frac{{a\sqrt {906} }}{{29}}\).
Trả lời:
Lời giải
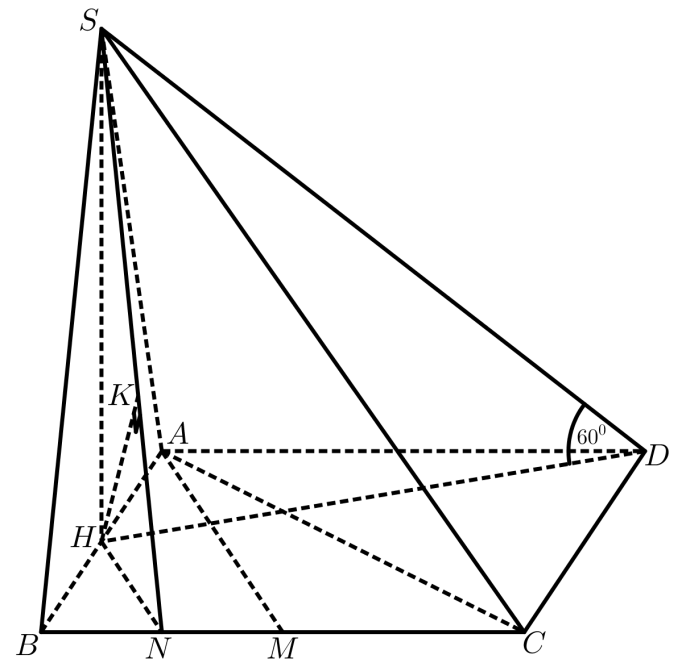
Gọi \(H\) là trung điểm \(AB.\) Theo giả thiết ta có \(SH \bot \left( {ABCD} \right).\)
Vì \(AC = a\) nên tam giác \(ABC\) đều.
Theo giả thiết \(\left( {SD,\,\,\left( {ABCD} \right)} \right) = \widehat {SDH} = 60^\circ .\)
Ta có \(AD{\rm{//}}BC \Rightarrow AD{\rm{//}}\left( {SBC} \right).\)
Khi đó \(d\left( {AD,\,\,SC} \right) = d\left( {AD,\,\,\left( {SBC} \right)} \right) = d\left( {A,\,\,\left( {SBC} \right)} \right) = 2d\left( {H,\,\,\left( {SBC} \right)} \right).\)
Gọi \(M\) là trung điểm \(BC \Rightarrow AM \bot BC.\)
Vẽ \(HN \bot BC\) (1) \(\left( {N \in BC} \right),\) \(HK \bot SN\) (2) \(\left( {K \in SN} \right).\)
\(SH \bot \left( {ABCD} \right) \Rightarrow SH \bot BC\) (3).
(1), (3) \( \Rightarrow BC \bot \left( {SHN} \right) \Rightarrow BC \bot HK\) (4).
(2), (4) \( \Rightarrow HK \bot \left( {SBC} \right).\)
Khi đó \(d\left( {H,\,\,\left( {SBC} \right)} \right) = HK.\)
\(HN = \frac{1}{2}AM = \frac{{a\sqrt 3 }}{4}.\)
\(H{D^2} = A{H^2} + A{D^2} – 2.AH.AD.\cos \widehat {HAD} = \frac{{7{a^2}}}{4} \Rightarrow HD = \frac{{a\sqrt 7 }}{2}.\)
\(\tan \widehat {SDH} = \frac{{SH}}{{HD}} \Leftrightarrow SH = HD.\tan \widehat {SDH} = \frac{{a\sqrt {21} }}{2}.\)
\(\frac{1}{{H{K^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{N^2}}} = \frac{1}{{{{\left( {\frac{{a\sqrt {21} }}{2}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{4}} \right)}^2}}} = \frac{{116}}{{21{a^2}}} \Rightarrow HK = \frac{{\sqrt {609} }}{{58}}a.\)
Vậy \(d\left( {AD,\,\,SC} \right) = 2.\frac{{\sqrt {609} }}{{58}}a = \frac{{\sqrt {609} a}}{{29}}.\)
Chọn đáp án B
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Bạn muốn mua một áo sơ mi cỡ 40 hoặc 41. Áo cỡ 40 có 6 màu khác nhau, áo cỡ 41 có 4 màu khác nhau. Hỏi bạn có bao nhiêu cách chọn?
Câu hỏi:
Bạn muốn mua một áo sơ mi cỡ 40 hoặc 41. Áo cỡ 40 có 6 màu khác nhau, áo cỡ 41 có 4 màu khác nhau. Hỏi bạn có bao nhiêu cách chọn?
A. \(24\).
B. \(10\).
Đáp án chính xác
C. \(45\).
D. \(50\).
Trả lời:
Lời giải
Chọn một áo sơ mi cỡ 40 có 6 cách.
Chọn một áo sơ mi cỡ 41 có 4 cách.
Theo qui tắc cộng, ta có: \(6 + 4 = 10\) cách chọn một áo sơ mi.
Chọn đáp án B====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu tiên \({u_1} = 2\) và công bội \(q = – 3\). Số số hạng thứ 4 của cấp số nhân bằng
Câu hỏi:
Cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu tiên \({u_1} = 2\) và công bội \(q = – 3\). Số số hạng thứ 4 của cấp số nhân bằng
A. \(24\).
B. \(54\).
C. \( – 54\).
Đáp án chính xác
D. \( – 24\).
Trả lời:
Lời giải
Số hạng tổng quát của cấp số nhân là: \({u_n} = {u_1}.{q^{n – 1}}\)
Số số hạng thứ 4 của cấp số nhân là: \({u_4} = 2.{\left( { – 3} \right)^3} = – 54\).
Chọn đáp án C====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Nghiệm của phương trình \({3^{1 – 2x}} = \frac{1}{3}\)là
Câu hỏi:
Nghiệm của phương trình \({3^{1 – 2x}} = \frac{1}{3}\)là
A. \(x = – 1\).
B. \(x = 0\).
C. \(x = 2\).
D. \(x = 1\).
Đáp án chính xác
Trả lời:
Lời giải
Ta có: \({3^{1 – 2x}} = \frac{1}{3} \Leftrightarrow {3^{1 – 2x}} = {3^{ – 1}} \Leftrightarrow 1 – 2x = – 1 \Leftrightarrow x = 1\).
Chọn đáp án D====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Thể tích của khối lăng trụ có đáy là hình vuông cạnh 2 và chiều cao 3 bằng
Câu hỏi:
Thể tích của khối lăng trụ có đáy là hình vuông cạnh 2 và chiều cao 3 bằng
A. \(4\).
B. \(12\).
Đáp án chính xác
C. \(8\).
D. \(18\).
Trả lời:
Lời giải
Ta có: \(V = h.B = {3.2^2} = 12\).
Chọn đáp án B====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tập xác định của hàm số \(y = {\log _3}\left( {4 – {x^2}} \right) + {2^{1 – 2x}}\) là
Câu hỏi:
Tập xác định của hàm số \(y = {\log _3}\left( {4 – {x^2}} \right) + {2^{1 – 2x}}\) là
A. \(D = \left( { – 2;2} \right)\).
Đáp án chính xác
B. \(D = \left[ { – 2;2} \right]\).
C. \(D = \left( {2; + \infty } \right)\).
D. \(D = \left( {4; + \infty } \right)\).
Trả lời:
Lời giải
Lưu ý:hàm số \(y = {\log _a}f\left( x \right)\) xác định khi và chỉ khi \(f\left( x \right) >0.\) Hàm số \(y = {a^x}\) xác định với mọi \(x \in \mathbb{R}.\)
Do đó: hàm số đã cho xác định khi và chỉ khi \(4 – {x^2} >0 \Leftrightarrow – 2 < x < 2\).
Chọn đáp án A====== **** mời các bạn xem câu tiếp bên dưới **** =====