Câu hỏi:
Tính diện tích phần gạch chéo trên hình vẽ sau.
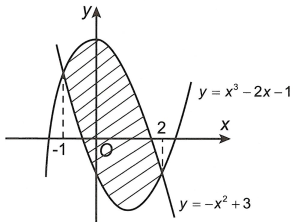
Trả lời:
Hướng dẫn giải
Từ đồ thị ta thấy
\( – {x^2} + 3 \ge {x^2} – 2x – 1\) \(\forall x \in \left[ { – 1;2} \right]\)
Vậy diện tích phần hình phẳng gạch chéo trong hình vẽ là \(S = \int\limits_{ – 1}^2 {\left[ {\left( { – {x^2} + 3} \right) – \left( {{x^2} – 2x – 1} \right)} \right]dx} \)
\( = \int\limits_{ – 1}^2 {\left( { – 2{x^2} + 2x + 4} \right)dx} \)
\( = \left( {\frac{{ – 2}}{3}{x^3} + {x^2} + 4x} \right)\left| \begin{array}{l}^2\\_{ – 1}\end{array} \right.\)
\( = \frac{3}{2}\)
====== **** mời các bạn xem câu tiếp bên dưới **** =====