Giả sử z1,z2là hai trong số các số phức z thỏa mãn iz+2-i=1 và z1-z2=2. Giá trị lớn nhất của bằng

Câu hỏi:

Giả sử $z_1,z_2$là hai trong số các số phức z thỏa mãn $\left|iz+\sqrt{2}–i\right|=1$ và $\left|z_1–z_2\right|=2$. Giá trị lớn nhất của bằng

A. 3

B. $2\sqrt{3}$

C. $3\sqrt{2}$

D. 4

Đáp án chính xác

Trả lời:

Đáp án D
Phương pháp:
+) Từ giả thiết , tìm ra đường biểu diễn (C) của các số phức z.
+) Gọi A, B lần lượt là điểm biểu diễn của
vị trí của AB đối với đường tròn (C).
 
+) Sử dụng công thức trung tuyến tính $O{A}^2+O{B}^2$
+) Sử dụng BĐT Bunhiascopsky tìm GTLN của OA+OB
Cách giải:
Ta có: 
với 

  M(x;y) biểu diễn z thuộc đường tròn tâm I($1;\sqrt{2}$)bán kính R=1.
Lại có:  
Mặt khác theo công thức trung tuyến ta có:
 
Theo BĐT Bunhiascopsky ta có:

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Hàm số y=x3-3x+1 đạt cực đại tại x bằng
   
   

   Câu hỏi:
   

   Hàm số $y=x^3–3x+1$ đạt cực đại tại $x$ bằng

   A. 2

   B. 1

   C. 0

   D. -1

   Đáp án chính xác

   Trả lời:

   Chọn D
   
   Lập bảng biến thiên 
   $\Rightarrow$Hàm số đạt cực đại tại x = -1

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Tìm giá trị cực đại yCĐ của hàm số y=-x4+2×2-5
   
   

   Câu hỏi:
   

   Tìm giá trị cực đại $y_{CĐ}$ của hàm số $y=–x^4+2x^2–5$

   A. -4

   Đáp án chính xác

   B. -5

   C. -2

   D. -6

   Trả lời:

   Chọn A
   
   Lập bảng biến thiên . Suy ra $y_{CĐ}=–4$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Hàm số y=13×3-2×2+4x-1 có bao nhiêu điểm cực trị? 
   
   

   Câu hỏi:
   

   Hàm số $y=\frac{1}{3}{x}^3–2x^2+4x–1$ có bao nhiêu điểm cực trị? 

   A. 1

   B. 0

   Đáp án chính xác

   C. 2

   D. 3

   Trả lời:

   Chọn B
   Phương pháp tự luận
   
   Hàm số không có cực trị

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hàm số y=x3-3×2+2. Khẳng định nào sau đây đúng
   
   

   Câu hỏi:
   

   Cho hàm số $y=x^3–3x^2+2$. Khẳng định nào sau đây đúng

   A. Hàm số có cực đại, cực tiểu 

   Đáp án chính xác

   B. Hàm số không có cực trị

   C. Hàm số có cực đại , không có cực tiểu

   D. Hàm số có cực tiểu không có cực đại

   Trả lời:

   Chọn A
   Phương pháp tự luận
   
   Vậy hàm số đạt CĐ tại x = 0, CT tại x = 2.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hàm số y=f(x) có bảng biến thiên như sau Khi đó hàm số đã cho có
   
   

   Câu hỏi:
   

   Cho hàm số $y=f\left(x\right)$ có bảng biến thiên như sau
   
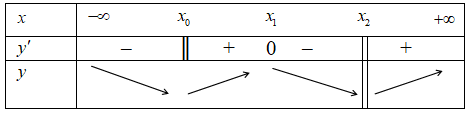
   Khi đó hàm số đã cho có

   A. Một điểm cực đại, một điểm cực tiểu

   Đáp án chính xác

   B. Một điểm cực đại , hai điểm cực tiểu

   C.1 điểm cực đại, không có điểm cực tiểu

   D.2 điểm cực đại , 1 điểm cực tiểu

   Trả lời:

   Chọn A

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====