Gọi z1, z2, z3, z4  là bốn nghiệm phức của phương trình z4 – z2 – 8 = 0. Trên mặt phẳng tọa độ z  gọi A , B , C , D lần lượt là bốn điểm biểu diễn bốn nghiệm z1, z2, z3, z4 đó. Tính giá trị của P = OA + OB + OC + OD, trong đó O là gốc tọa độ.

Câu hỏi:

Gọi $z_1, z_2, z_3, z_4$  là bốn nghiệm phức của phương trình $z^4 – z^2$ – 8 = 0. Trên mặt phẳng tọa độ z  gọi A , B , C , D lần lượt là bốn điểm biểu diễn bốn nghiệm $z_1, z_2, z_3, z_4$ đó. Tính giá trị của P = OA + OB + OC + OD, trong đó O là gốc tọa độ.

A. P = 4

B. P = 2 + $\sqrt{2}$

C. P = 2$\sqrt{2}$

D. P = 4 + 2$\sqrt{2}$

Đáp án chính xác

Trả lời:

Đáp án D

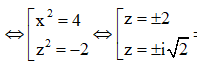
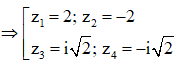
Khi đó 

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho số phức z thỏa mãn: |z – 1 + i| = 2. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức z là:
   
   

   Câu hỏi:
   

   Cho số phức z thỏa mãn: |z – 1 + i| = 2. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức z là:

   A. Một đường thẳng.

   B. Một đường Parabol.

   C. Một đường tròn có bán kính bằng 2.

   Đáp án chính xác

   D. Một đường tròn có bán kính bằng 4.

   Trả lời:

   Đáp án C
   Cách 1: Số phức z được biểu diễn bởi điểm M(x;y).
   Số phức z₁ được biểu diễn bởi điểm A(1;-1).
   Em có: |z – 1 + i| = 2 => MA = 2
   Vậy tập hợp điểm M là đường tròn tâm A(1;-1), bán kính R = 2 và có phương trình: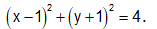
   Cách 2: Đặt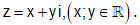 . Số phức z được biểu diễn bởi điểm M(x;y).
   Em có:
   
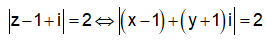
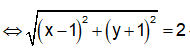
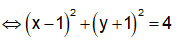
   Vậ tập hợp điểm M là đường tròn tâm I(1;-1), bán kính R = 2 và có phương trình: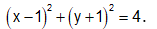 

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho 2 số phức z1 và z2 thỏa mãn: |z1 – 5 – i| = 3|z2 + 5 – 2i| = |iz2 – 3|. Giá trị nhỏ nhất của biểu thức P = |z1 – z2| là:
   
   

   Câu hỏi:
   

   Cho 2 số phức z₁ và z₂ thỏa mãn: |z₁ – 5 – i| = 3|z₂ + 5 – 2i| = |iz₂ – 3|. Giá trị nhỏ nhất của biểu thức P = |z₁ – z₂| là:

   A. -3 – 3$\sqrt{2}$

   B. 3 + 3$\sqrt{2}$

   C. 3 – 3$\sqrt{2}$

   D. -3 + 3$\sqrt{2}$

   Đáp án chính xác

   Trả lời:

   Đáp án D
   Đặt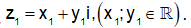 Số phức z được biểu diễn bởi điểm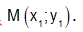
   Đặt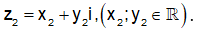 Số phức z₂ được biểu diễn bởi điểm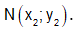
   Suy ra: |z₁ – z₂| = MN
   Em có: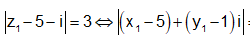 
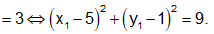
   Vậy điểm M thuộc đường tròn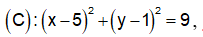 có tâm là điểm I(5;1) bán kính R = 3
   Em có
   
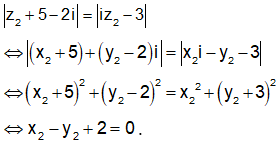
   Vậy điểm N thuộc đường thẳng d: x – y + 2 = 0.
   Dễ thấy đường thẳng d và đường tròn C không cắt nhau.
   
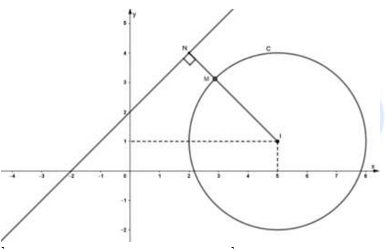
   Áp dụng bất đẳng thức tam giác cho bộ ba điểm I, M, N em có:
   
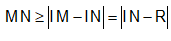
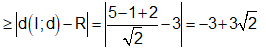
   Dấu “=” bằng xảy ra khi và chỉ khi I, M, N thẳng hàng và N là hình chiếu của I trên đường thẳng d.
   Vậy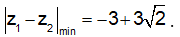 

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho số phức z = a + bi(a,b∈ℝ) thỏa mãn z + 2 + i – |z|(i+1) = 0 và |z| > 1. Tính P = a + b
   
   

   Câu hỏi:
   

   Cho số phức z = a + bi(a,b$\in \mathrm{ℝ}$) thỏa mãn z + 2 + i – |z|(i+1) = 0 và |z| > 1. Tính P = a + b

   A. P = -1

   B. P = -5

   C. P = 3

   D. P = 7

   Đáp án chính xác

   Trả lời:

   Đáp án D
   Đặt z = a + bi
   
   
   
   

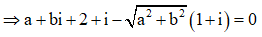
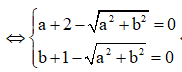
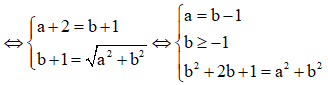
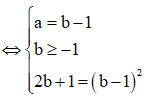
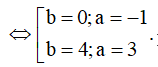
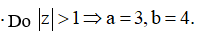
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Xét các số phức z = a +  bi(a,b∈ℝ) thỏa mãn điều kiện |z – 4 – 3i| = 5. Tính P = a + b khi giá trị biểu thức |z + 1 – 3i + |z – 1 + i|| đạt giá trị lớn nhất.
   
   

   Câu hỏi:
   

   Xét các số phức z = a +  bi(a,b$\in \mathrm{ℝ}$) thỏa mãn điều kiện |z – 4 – 3i| = $\sqrt{5}$. Tính P = a + b khi giá trị biểu thức |z + 1 – 3i + |z – 1 + i|| đạt giá trị lớn nhất.

   A. P = 10

   Đáp án chính xác

   B. P = 4

   D. P = 6

   D. P = 8

   Trả lời:

   Đáp án A
   Gọi M(x;y) là điểm biều diễn số phức z.
   Từ giả thiết, ta có |z – 4 – 3i| =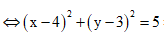 $\sqrt{5}$ 
   => M thuộc đường tròn (C) tâm I(4;3), bán kính R =  $\sqrt{5}$
   Khi đó P = MA + MB với A(-1;3), B(1;-1)
   Ta có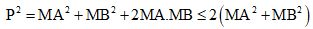
   Gọi E(0;1) là trung điểm của AB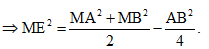 
   Do đó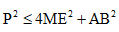  mà 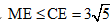 suy ra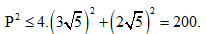 
    
   Với C là giao điểm của đường thẳng EI với đường tròn (C)
   Vậy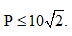 Dấu “=”xảy ra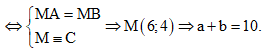  

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho số phức z thỏa mãn điều kiện (1+i)z¯ – 1 – 3i = 0. Tìm phần ảo của số phức w = 1 – zi + z¯
   
   

   Câu hỏi:
   

   Cho số phức z thỏa mãn điều kiện (1+i)$\overline{z}$ – 1 – 3i = 0. Tìm phần ảo của số phức w = 1 – zi + $\overline{z}$

   A. -i

   B. -1

   Đáp án chính xác

   C. 2

   D. -2i

   Trả lời:

   Đáp án C
   giả sử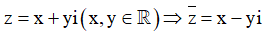 
   The giả thiết, ta có 
   
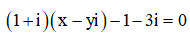
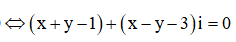
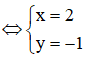
   Suy ra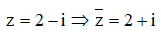 
   Ta có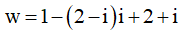 
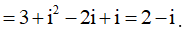
   Vậy chọn phần ảo là – 1 

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====