Từ một tấm tôn dạng hình tròn với bán kính \(R = 50cm\), một anh thợ cần cắt một tấm tôn có dạng hình chữ nhật nội tiếp hình tròn trên. Anh ta gò tấm tôn hình chữ nhật này thành một hình trụ không đáy (như hình vẽ) để thả gà vào trong. Thể tích lớn nhất của khối trụ thu được gần nhất với kết quả nào dưới đây?

Câu hỏi:

Từ một tấm tôn dạng hình tròn với bán kính \(R = 50cm\), một anh thợ cần cắt một tấm tôn có dạng hình chữ nhật nội tiếp hình tròn trên. Anh ta gò tấm tôn hình chữ nhật này thành một hình trụ không đáy (như hình vẽ) để thả gà vào trong. Thể tích lớn nhất của khối trụ thu được gần nhất với kết quả nào dưới đây?

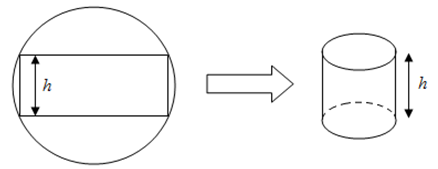
A. 0,28m³                  

B. 0,02m³                  

C. 0,29m³                  

D. 0,03m³

Đáp án chính xác

Trả lời:

Đáp án D
Khối trụ thu được có thể tích là \(V = \pi {r^2}h\).
Gọi chiều dài của hình chữ nhật là \(b \Rightarrow {b^2} + {h^2} = {\left( {2R} \right)^2} = 1m\left( {R = 0,5m} \right)\)
Ta có
$2r\pi =b\Rightarrow r=\frac{b}{2\pi }=\frac{\sqrt{1-h^2}}{2\pi }\Rightarrow V=\pi .\frac{1-h^2}{4{\pi }^2}.h=\frac{h-h^3}{4\pi }=f\left(h\right)$
Lại có \({h^3} + {\left( {\frac{1}{{\sqrt 3 }}} \right)^3} + {\left( {\frac{1}{{\sqrt 3 }}} \right)^3} \ge 3h.\frac{1}{{\sqrt 3 }}.\frac{1}{{\sqrt 3 }} = h \Rightarrow h – {h^3} \le \frac{2}{{3\sqrt 3 }}\)
\( \Rightarrow V \le \frac{2}{{4\pi .3\sqrt 3 }} = \frac{1}{{6\pi \sqrt 3 }} \approx 0,03{m^3}\). Chọn D.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Với a là số thực dương tùy ý, \({\log _2}\left( {8a} \right)\) bằng
   
   

   Câu hỏi:
   

   Với a là số thực dương tùy ý, \({\log _2}\left( {8a} \right)\) bằng

   A. \(3 + {\log _2}a\)   

   Đáp án chính xác

   B. \(4 + {\log _2}a\)   

   C. \(8{\log _2}a\)       

   D. \(3{\log _2}a\)

   Trả lời:

   Đáp án A
   Ta có \({\log _2}\left( {8a} \right) = {\log _2}8 + {\log _2}a = 3 + {\log _2}a\). Chọn A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Trong không gian Oxyz, cho mặt phẳng P:3x−4y+5z−2=0. Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
   
   

   Câu hỏi:
   

   Trong không gian Oxyz, cho mặt phẳng $\left(P\right):3x-4y+5z-2=0$. Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?

   A. $\overrightarrow{n}=\left(-4;5;-2\right)$

   B. $\overrightarrow{n}=\left(3;-4;2\right)$

   C. $\overrightarrow{n}=\left(3;-5;-2\right)$

   D. $\overrightarrow{n}=\left(3;-4;5\right)$

   Đáp án chính xác

   Trả lời:

   Đáp án D
   Mặt phẳng $\left(P\right):3x-4y+5z-2=0$ có một VTPT là $\overrightarrow{n}=\left(3;-4;5\right)$. Chọn D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Số phức \(z = 2 – 3i\) có phần ảo bằng
   
   

   Câu hỏi:
   

   Số phức \(z = 2 – 3i\) có phần ảo bằng

   A. 2.                          

   B. \( – 3\)                    

   Đáp án chính xác

   C. \( – 2\)                   

   D. \( – 3i\)

   Trả lời:

   Đáp án B
   Số phức \(z = 2 – 3i\) có phần ảo bằng \( – 3\). Chọn B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho cấp số cộng \(\left( {{u_n}} \right)\) với \({u_2} = 6,{u_5} = 21\). Tính d.
   
   

   Câu hỏi:
   

   Cho cấp số cộng \(\left( {{u_n}} \right)\) với \({u_2} = 6,{u_5} = 21\). Tính d.

   A. \(d = 3\)                

   B. \(d = 2\)                 

   C. \(d = 4\)                

   D. \(d = 5\)

   Đáp án chính xác

   Trả lời:

   Đáp án D
   Ta có \(\left\{ \begin{array}{l}{u_2} = 6\\{u_5} = 21\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} + d = 6\\{u_1} + 4d = 21\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} = 1\\d = 5\end{array} \right. \Rightarrow \)Chọn D

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau: Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
   
   

   Câu hỏi:
   

   Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
   
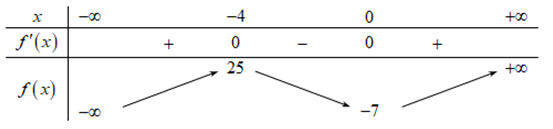
   Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

   A. \(\left( { – 7;25} \right)\)                         

   B. \(\left( { – \infty ; – 4} \right)\)    

   C. \(\left( { – 4;0} \right)\)              

   Đáp án chính xác

   D. \(\left( {0; + \infty } \right)\)

   Trả lời:

   Đáp án C
   Hàm số \(f\left( x \right)\) nghịch biến trên \(\left( { – 4;0} \right)\). Chọn C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====