Câu hỏi:
Trong không gian với hệ tọa độ Oxyz,cho mặt phẳng \(\left( P \right):2x – y + z – 6 = 0\) và đường thẳng \(d:\frac{{x + 2}}{2} = \frac{{y – 1}}{1} = \frac{{z – 1}}{{ – 1}}.\) Viết phương trình đường thẳng Δ cắt mặt phẳng (P) và đường thẳng d lần lượt tại M và N sao cho \(A\left( {3;5;2} \right)\) là trung điểm của cạnh MN.
A.\(\Delta :\frac{x}{3} = \frac{{y – 2}}{3} = \frac{z}{2}.\)
B.\(\Delta :\frac{{x – 2}}{1} = \frac{{y – 3}}{2} = \frac{{z + 1}}{3}.\)
Đáp án chính xác
C.\(\Delta :\frac{{x + 6}}{9} = \frac{{y + 1}}{6} = \frac{{z – 3}}{{ – 1}}.\)
D.\(\Delta :\frac{{x – 4}}{{ – 1}} = \frac{{y – 4}}{1} = \frac{{z + 2}}{4}.\)
Trả lời:
Lời giải:
Chọn đáp án B
Ta có: \(d:\left\{ \begin{array}{l}x = – 2 + 2t\\y = 1 + t\\z = 1 – t\end{array} \right.{\rm{ }}\left( {t \in \mathbb{R}} \right)\) mà \(N \in d \Rightarrow N\left( {2t – 2;t + 1;1 – t} \right)\).
Bài ra \(A\left( {3;5;2} \right)\)là trung điểm của cạnh MN
\( \Rightarrow M\left( {6 – 2t + 2;10 – t – 1;4 – 1 + t} \right) \Rightarrow M\left( {8 – 2t;9 – t;t + 3} \right)\)
Mà \(M \in \left( P \right) \Rightarrow 2\left( {8 – 2t} \right) – \left( {9 – t} \right) + \left( {t + 3} \right) – 6 = 0 \Leftrightarrow – 2t + 4 = 0 \Leftrightarrow t = 2 \Rightarrow N\left( {2;3; – 1} \right).\)
Đường thẳng \(\Delta \) qua \(N\left( {2;3; – 1} \right)\) và nhận \(\overrightarrow {NA} = \left( {1;2;3} \right)\)là một VTCP
\( \Rightarrow \Delta :\frac{{x – 2}}{1} = \frac{{y – 3}}{2} = \frac{{z + 1}}{3}\).
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian Oxyz,cho mặt phẳng \(\left( P \right):x – 6y + 12z – 5 = 0.\) Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
Câu hỏi:
Trong không gian Oxyz,cho mặt phẳng \(\left( P \right):x – 6y + 12z – 5 = 0.\) Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
A.\(\vec n = \left( {1; – 6;12} \right).\)
Đáp án chính xác
B.\(\vec n = \left( {1;6;12} \right).\)
C.\(\vec n = \left( { – 1;6;12} \right).\)
D.\(\vec n = \left( {1;6; – 12} \right).\)
Trả lời:
Lời giải:
Chọn đáp án A
Mặt phẳng \(\left( P \right):x – 6y + 12{\rm{z}} – 5 = 0\)có một VTPT là \(\overrightarrow n = \left( {1; – 6;12} \right)\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số f(x) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Câu hỏi:
Cho hàm số f(x) có bảng biến thiên như sau:
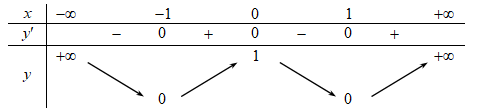
Hàm số đã cho đồng biến trên khoảng nào dưới đây?A.\(\left( { – 1;0} \right).\)
Đáp án chính xác
B.\(\left( {0;1} \right).\)
C.\(\left( {0; + \infty } \right).\)
D.\(\left( { – 1;1} \right).\)
Trả lời:
Lời giải:
Chọn đáp án A
Hàm số \(f\left( x \right)\)đồng biến trên \(\left( { – 1;0} \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số f(x) có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho là
Câu hỏi:
Cho hàm số f(x) có bảng biến thiên như sau:
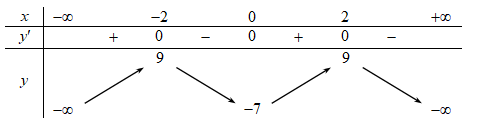
Giá trị cực đại của hàm số đã cho làA.0.
B.9.
Đáp án chính xác
C.−7.
D.2.
Trả lời:
Lời giải:
Chọn đáp án B
Giá trị cực đại của hàm số \(f\left( x \right)\)là 9.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hai số phức \({z_1} = 1 + 2i,{\rm{ }}{z_2} = 2 – 3i.\) Số phức \(w = {z_1} – {z_2}\) có phần ảo bằng
Câu hỏi:
Cho hai số phức \({z_1} = 1 + 2i,{\rm{ }}{z_2} = 2 – 3i.\) Số phức \(w = {z_1} – {z_2}\) có phần ảo bằng
A.5.
Đáp án chính xác
B.1.
C.\( – 5.\)
D.\(5i.\)
Trả lời:
Lời giải:
Chọn đáp án A
Số phức \({\rm{w}} = {z_1} – {z_2} = – 1 + 5i\)có phần ảo bằng 5.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho \(a,{\rm{ }}b,{\rm{ }}x\) là các số thực dương tùy ý thỏa mãn \({\log _2}x = 2{\log _2}a + 3{\log _2}b.\) Mệnh đề nào dưới đây là đúng?
Câu hỏi:
Cho \(a,{\rm{ }}b,{\rm{ }}x\) là các số thực dương tùy ý thỏa mãn \({\log _2}x = 2{\log _2}a + 3{\log _2}b.\) Mệnh đề nào dưới đây là đúng?
A.\(x = {a^2}{b^3}.\)
Đáp án chính xác
B.\(x = {a^2} + {b^3}.\)
C.\(x = 2a + 3b.\)
D.\(x = 3a + 2b.\)
Trả lời:
Lời giải:
Chọn đáp án A
Ta có \({\log _2}x = 2{\log _2}a + 3{\log _2}b = {\log _2}{a^2} + {\log _2}{b^3} = {\log _2}\left( {{a^2}{b^3}} \right) \Rightarrow x = {a^2}{b^3}.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====