Câu hỏi:
Trong không gian Oxyz, cho mặt \(\left( S \right):{x^2} + {y^2} + {z^2} – 2x + 4y + 4z = 0\) và điểm \(M\left( {1;2; – 1} \right).\) Một đường thẳng thay đổi qua M và cắt \(\left( S \right)\) tại hai điểm phân biệt \(A,{\rm{ }}B.\) Tìm giá trị lớn nhất của tổng \(MA + MB.\)
A. 8.
B. 10.
C. \(2\sqrt {17} .\)
Đáp án chính xác
D. \(8 + 2\sqrt 5 .\)
Trả lời:
Đáp án C
Mặt cầu \(\left( S \right):{\left( {x – 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z + 2} \right)^2} = 9\) có tâm \(I\left( {1; – 2; – 2} \right)\), bán kính \(R = 3\).
Gọi d là đường thẳng thay đổi qua M và cắt \(\left( S \right)\) tại hai điểm phân biệt A, B.
Ta có \(\overrightarrow {MI} = \left( {0; – 4; – 1} \right) \Rightarrow MI = \sqrt {17} > R \Rightarrow M\) nằm ngoài \(\left( S \right)\).
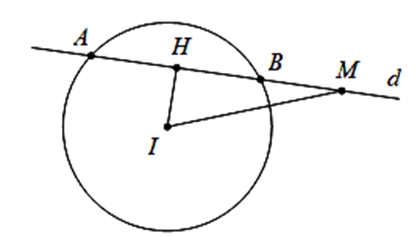
Gọi H là trung điểm của cạnh AB.
Ta có \(MA + MB = \left( {MH + HA} \right) + MB = MH + HB + MB = MH + HM = 2MH \le 2MI = 2\sqrt {17} .\)
Dấu “=” xảy ra \( \Leftrightarrow d\) qua I.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho a là số thực dương tùy ý và \(a \ne 1.\) Mệnh đề nào dưới đây là đúng?
Câu hỏi:
Cho a là số thực dương tùy ý và \(a \ne 1.\) Mệnh đề nào dưới đây là đúng?
A. \({\log _3}a = {\log _a}3.\)
B. \({\log _3}a = \frac{1}{{{{\log }_3}a}}.\)
C. \({\log _3}a = \frac{1}{{{{\log }_a}3}}.\)
Đáp án chính xác
D. \({\log _3}a = – {\log _a}3.\)
Trả lời:
Đáp án C
Ta có \({\log _3}a = \frac{1}{{{{\log }_a}3}}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Điểm nào trong hình vẽ bên là điểm biểu diễn số phức \(z = – 1 – 2i\)?
Câu hỏi:
Điểm nào trong hình vẽ bên là điểm biểu diễn số phức \(z = – 1 – 2i\)?
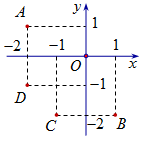
A. Điểm A.
B. Điểm B.
C. Điểm C.
Đáp án chính xác
D. Điểm D.
Trả lời:
Đáp án C
Điểm biểu diễn số phức \(z = – 1 – 2i\) có tọa độ \(\left( { – 1;2} \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho \(\int\limits_0^1 {f\left( x \right)dx} = 2\) và \(\int\limits_1^2 {f\left( x \right)dx} = – 3.\) Tích phân \(\int\limits_0^2 {f\left( x \right)dx} \) bằng
Câu hỏi:
Cho \(\int\limits_0^1 {f\left( x \right)dx} = 2\) và \(\int\limits_1^2 {f\left( x \right)dx} = – 3.\) Tích phân \(\int\limits_0^2 {f\left( x \right)dx} \) bằng
A. 5.
B. \( – 5.\)
C. 1.
D. \( – 1.\)
Đáp án chính xác
Trả lời:
Đáp án D
Ta có \(\int\limits_0^2 {f\left( x \right)d{\rm{x}}} = \int\limits_0^1 {f\left( x \right)d{\rm{x}}} + \int\limits_1^2 {f\left( x \right)d{\rm{x}}} = – 1\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian Oxyz, cho hai điểm \(A\left( {2;3;4} \right),{\rm{ }}B\left( {6;2;2} \right).\) Tìm tọa độ của vectơ \(\overrightarrow {AB} .\)
Câu hỏi:
Trong không gian Oxyz, cho hai điểm \(A\left( {2;3;4} \right),{\rm{ }}B\left( {6;2;2} \right).\) Tìm tọa độ của vectơ \(\overrightarrow {AB} .\)
A. \(\overrightarrow {AB} = \left( {4;3;4} \right).\)
B. \(\overrightarrow {AB} = \left( {4; – 1; – 2} \right).\)
Đáp án chính xác
C. \(\overrightarrow {AB} = \left( { – 2;3;4} \right).\)
D. \(\overrightarrow {AB} = \left( {4; – 1;4} \right).\)
Trả lời:
Đáp án B
Ta có \(\overrightarrow {AB} = \left( {4; – 1; – 2} \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ ?
Câu hỏi:
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ ?
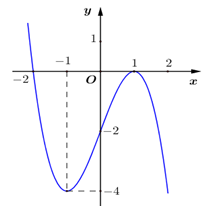
A. \(y = {x^3} – 3{x^2} – 2.\)
B. \(y = {x^3} – 3x – 2.\)
C. \(y = – {x^3} + 3{x^2} – 2.\)
D. \(y = – {x^3} + 3x – 2.\)
Đáp án chính xác
Trả lời:
Đáp án D
Ta có \(y\left( 1 \right) = 0 \Rightarrow \) Loại A và B. Mà \(y\left( { – 1} \right) = – 4\).====== **** mời các bạn xem câu tiếp bên dưới **** =====