Tìm các số thực b,c để phương trình z2 + bz + c = 0  nhận z = 1+ i làm một nghiệm.

Câu hỏi:

Tìm các số thực b,c để phương trình z² + bz + c = 0  nhận z = 1+ i làm một nghiệm.

A. b = -2; c = 3

B. b = -1; c = 2

C. b = -2; c = 2

Đáp án chính xác

D. b = 2; c = 2

Trả lời:

Chọn C.
Theo giả thiết phương trình nhận z = 1+ i làm một nghiệm của phương trình: z² + bz + c = 0.
Nên ( 1 + i) ² + b(1 + i) + c = 0
Hay b + c + ( 2 + b) i = 0
Do đó: b + c = 0 và 2 + b = 0
Ta tìm được : b = -2 và c = 2.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Tìm số phức z thỏa mãn hệ thức z-2+i=10 và z.z¯=25
   
   

   Câu hỏi:
   

   Tìm số phức z thỏa mãn hệ thức $\left|z–\left(2+i\right)\right|=\sqrt{10}$ và $z.\overline{z}=25$

   A. z = 3 + 4i; z = 5.

   Đáp án chính xác

   B. z = 3 + 4i; z = -4.

   C. z = -3 + 4i; z = 5.

   D. z = 3 – 4i; z = -5.

   Trả lời:

   Chọn  A.
   Gọi z = a + bi khi đó 
   
   Hay (a – 2)² + (b – 1)² = 10
    
   Từ (*) và (**)  
   Vậy z = 3 + 4i hoặc z = 5.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Tìm số thực x; y để hai số phức z1 = 9y2 – 4 – 10xi5 và z2 = 8y2 + 20i11 là liên hợp của nhau?
   
   

   Câu hỏi:
   

   Tìm số thực x; y để hai số phức z₁ = 9y² – 4 – 10xi⁵ và z₂ = 8y² + 20i¹¹ là liên hợp của nhau?

   A. x = -2; y = 2.

   B. x = 2; y = ±2.

   C. x = 2; y = 2.

   D. x = -2; y = ±2.

   Đáp án chính xác

   Trả lời:

   Chọn D.
   
   + z₁ và z₂ là liên hợp của nhau khi và chỉ khi:
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho số phức z thỏa mãn z2 – 6z + 13 = 0 . Giá trị của z+6z+i là:
   
   

   Câu hỏi:
   

   Cho số phức z thỏa mãn z² – 6z + 13 = 0 . Giá trị của $\left|z+\frac{6}{z+i}\right|$ là:

   A. $\sqrt{17} hoặc 5$

   Đáp án chính xác

   B. $–\sqrt{17} hoặc \sqrt{5}$

   C. $\sqrt{17} hoặc 4$

   D. $\sqrt{17} hoặc \sqrt{5}$

   Trả lời:

   Chọn A.
   

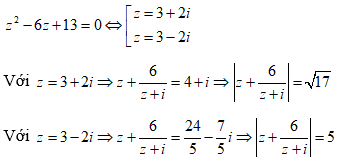
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho số phức z thỏa z=1-i1+i2016. Viết z dưới dạng z = a + bi. Khi đó tổng a + b có giá trị bằng bao nhiêu?
   
   

   Câu hỏi:
   

   Cho số phức z thỏa $z={\left(\frac{1–i}{1+i}\right)}^{2016}$. Viết z dưới dạng z = a + bi. Khi đó tổng a + b có giá trị bằng bao nhiêu?

   A. 3.

   B. -1.

   C. 1.

   Đáp án chính xác

   D. 2.

   Trả lời:

   Chọn  C.
   Ta có: 
   
   
   Khi đó: z = 1 + 0. i 
   Do đó a = 1 và b = 0 
   Nên a + b = 1 + 0 = 1.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Có bao nhiêu số phức z thỏa mãn: z2+z¯2=26 và z+z¯=6
   
   

   Câu hỏi:
   

   Có bao nhiêu số phức z thỏa mãn: ${\left|z\right|}^2+{\left|\overline{z}\right|}^2=26$ và $z+\overline{z}=6$

   A. 2.

   Đáp án chính xác

   B. 3.

   C. 0.

   D. 1.

   Trả lời:

   Chọn A.
   Đặt z = x + iy (x, y ∈ R), ta có 
   Ta có:
   
   ⇒ có 2 số phức thỏa yêu cầu đề bài.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====