Tập hợp các điểm biểu diễn số phức z thỏa mãn 2|z-1| = |z + z¯ +2| trên mặt phẳng tọa độ là một

Câu hỏi:

Tập hợp các điểm biểu diễn số phức z thỏa mãn 2|z-1| = |z + $\overline{z}$ +2| trên mặt phẳng tọa độ là một

A. đường thẳng.

B. đường tròn.

C. parabol.

Đáp án chính xác

D. hypebol.

Trả lời:

Đáp án C.
Đặt z = a + bi 
Ta có: 
Vậy quỹ tích là một parabol

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho số phức z thỏa mãn |z – 2 – 3i| = 1. Gọi M = max|z¯ + 1 + i|. Tính giá trị của biểu thức  
   
   

   Câu hỏi:
   

   Cho số phức z thỏa mãn |z – 2 – 3i| = 1. Gọi M = max|$\overline{z}$ + 1 + i|. Tính giá trị của biểu thức  

   A. $M^2 +\hspace{0.17em}{m}^2$ = 28

   Đáp án chính xác

   B. $M^2 +\hspace{0.17em}{m}^2$ = 26

   C. $M^2 +\hspace{0.17em}{m}^2$ = 24

   D. $M^2 +\hspace{0.17em}{m}^2$ = 20

   Trả lời:

    Đáp án A.
   Ta có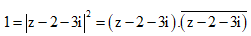 
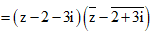
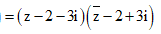
   Lấy môđun hai vế, ta được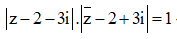
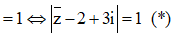
   Đặt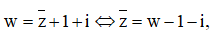 khi đó (*)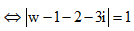 
   

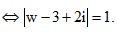
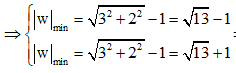
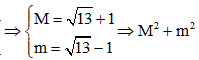
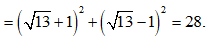
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho số phức z thỏa mãn  z-12-i+i = 5. Biết rằng tập hợp biểu diễn số phức w = (1-i)z + 2i có dạng (x+2)2 + y2 = k  Tìm k.
   
   

   Câu hỏi:
   

   Cho số phức z thỏa mãn  $\left|\frac{z–1}{2–i}+i\right| = \sqrt{5}$. Biết rằng tập hợp biểu diễn số phức w = (1-i)z + 2i có dạng ${(x+2)}^2 + y^2 = k$  Tìm k.

   A. k = 92

   B. k = 92

   C. k = 50

   Đáp án chính xác

   D. k = 96

   Trả lời:

   Đáp án C.
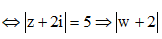
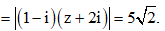
   Ta có $\left|\frac{z–1}{2–i}+i\right| = \sqrt{5}$ 
   Vậy tập hợp điểm biểu diễn số phức w là đường tròn tâm I(-2;0) bán kính R = 5$\sqrt{2}$ tức là đường tròn (C): ${(x+2)}^2 + y^2$ = 50

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Kí hiệu z0 là nghiệm phức có phần thực âm và phần ảo dương của phương trình z2 + 2z + 10 = 0. Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn số phức w = i2017z0?
   
   

   Câu hỏi:
   

   Kí hiệu $z_0$ là nghiệm phức có phần thực âm và phần ảo dương của phương trình $z^2$ + 2z + 10 = 0. Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn số phức w = $i^{2017}{z}_0$?

   A. M(3;-1)

   B. M(3;1)

   C. M(-3;1)

   D. M(-3;-1)

   Đáp án chính xác

   Trả lời:

   Đáp án D.
   Ta có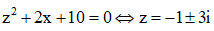 

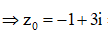
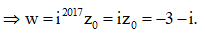
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Tìm số phức liên hợp của số phức z = (1-i)(3 + 2i)
   
   

   Câu hỏi:
   

   Tìm số phức liên hợp của số phức z = (1-i)(3 + 2i)

   A. $\overline{z}$ = 1 + i

   B. $\overline{z}$ = 5 + i

   Đáp án chính xác

   C. $\overline{z}$ = 5 – i

   D. $\overline{z}$ = 1 – i

   Trả lời:

   Đáp án B.
   Ta có z = (1-i)(3+2i) = 5 – i => $\overline{z}$ = 5 + i

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho số phức z thỏa mãn |z – 3 – 4i| = 5. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = |z+2|2 – |z-i|2. Tính môđun của số phức w = M + mi ?
   
   

   Câu hỏi:
   

   Cho số phức z thỏa mãn |z – 3 – 4i| = $\sqrt{5}$. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = $|z+2{|}^2 – |z–i{|}^2$. Tính môđun của số phức w = M + mi ?

   A. |w| = $\sqrt{2315}$

   B. |w| = $\sqrt{1258}$

   Đáp án chính xác

   C. |w| = $3\sqrt{137}$

   D. |w| = $2\sqrt{309}$

   Trả lời:

   Đáp án B.
   Đặt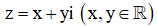  suy ra tập hợp các điểm M(z) = (x;y)  là đường tròn (C) có tâm I(3;4) và bán kính R = $\sqrt{5}$
   Ta có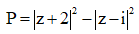 
   
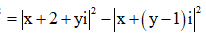
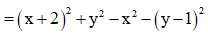
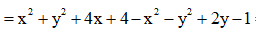
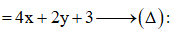
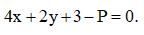
   Ta cần tìm P sao cho đường thẳng $∆$  và đường tròn (C) có điểm chung 
   
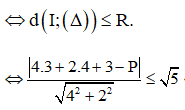
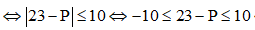
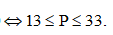
   Do đó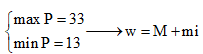 

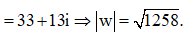
   ====== **** mời các bạn xem câu tiếp bên dưới **** =====