Số nghiệm của phương trình với ẩn số phức z: 4z2 + 8|z|2 – 3 = 0 là:

Câu hỏi:

Số nghiệm của phương trình với ẩn số phức z: 4z² + 8|z|² – 3 = 0 là:

A. 3.

B. 2.

C. 4.

Đáp án chính xác

D. 1.

Trả lời:

Chọn C.
Gọi z = a + bi  là nghiệm của phương trình.
Ta có: 4(a + bi) ² + 8(a² + b²) – 3 = 0 
$\iff$4(a² – b² + 2abi) + 8( a² + b²) – 3 = 0
$\iff$12a² + 4b² +8abi – 3 = 0



$\iff \left\{\begin{array}{l}\left[\begin{array}{c}a=0\\ b=\pm 1\end{array}\right.\\ \left[\begin{array}{c}a=\pm \frac{1}{2}\\ b=0\end{array}\right.\end{array}\right.$
Vậy phương trình có 4 nghiệm.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hai số phức z1; z2 khác 0 thỏa mãn z13+z23=0.Gọi A; B  lần lượt là các điểm biểu diễn cho số phức z1; z2. Khi đó tam giác OAB là:
   
   

   Câu hỏi:
   

   Cho hai số phức z₁; z₂ khác 0 thỏa mãn $z_1^3+z_2^3=0$.Gọi A; B  lần lượt là các điểm biểu diễn cho số phức z₁; z₂. Khi đó tam giác OAB là:

   A. Tam giác đều.

   Đáp án chính xác

   B. Tam giác vuông tại O.

   C. Tam giác tù.

   D. Tam giác có một góc bằng 45^o.

   Trả lời:

   Chọn A.
   Ta có ,
   suy ra:
   
   Lại có
   
   nên 
   Suy ra  AB = OA= OB
   Do đó. Tam giác OAB là tam giác đều.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho số phức z thỏa mãn (2z-1) ( 1+ i) +(z¯ + 1)(1-i) =2-2i. Giá trị của |z| là ?
   
   

   Câu hỏi:
   

   Cho số phức z thỏa mãn $(2z–1) ( 1+ i) +(\overline{z} + 1)(1–i) =2–2i$. Giá trị của |z| là ?

   A. $\frac{\sqrt{2}}{3}$

   Đáp án chính xác

   B. 2.

   C. $\frac{\sqrt{3}}{2}$

   D. $\frac{\sqrt{2}}{2}$

   Trả lời:

   Chọn A.
   Gọi z = a + bi  ta có : 
   
   
   
   
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho số phức z = a + bi thỏa mãn  .Tính P = a + b
   
   

   Câu hỏi:
   

   Cho số phức z = a + bi thỏa mãn 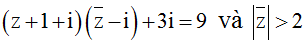 .Tính P = a + b

   A. -3.

   B. -1.

   C. 1.

   Đáp án chính xác

   D. 2.

   Trả lời:

   Chọn C.
   Đặt z = a + bi.
   Theo giải thiết ta có:
   [(a + 1) + (b + 1)i](a – bi – i) + 3i = 9
   Suy ra : a( a + 1) + ( b + 1) ² + a( b + 1) i – ( a + 1) ( b + 1) i = 9 – 3i
   Hay a(a + 1) + ( b + 1) ² – ( b +1) i = 9 -3i
   Ta có hệ 
   
   Do  nên a = -1; b = 2 
   Vậy P = a + b = 1.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Gọi z1 ; z2 ; z3 ; z4 là các nghiệm phức của phương trình . Giá trị của là:
   
   

   Câu hỏi:
   

   Gọi z₁ ; z₂ ; z₃ ; z₄ là các nghiệm phức của phương trình .
   Giá trị của là:

   A. 17/8

   B. 17/9

   Đáp án chính xác

   C. 9/17

   D. 17i/9

   Trả lời:

   Với mọi z ≠ i/2, ta có:
   
   
   
   
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho số phức z; w thỏa mãn |z – 1 + 2i| = |z + 5i| ; w = iz + 20.  Giá trị nhỏ nhất m của |w| là?
   
   

   Câu hỏi:
   

   Cho số phức z; w thỏa mãn |z – 1 + 2i| = |z + 5i| ; w = iz + 20.  Giá trị nhỏ nhất m của |w| là?

   

   

   Đáp án chính xác

   

   

   Trả lời:

   Chọn B.
   
   Gọi z = x + yi thì M(x; y)  là điểm biểu diễn z.
   Gọi A(1; -2) và B(0; -5), ta có tập hợp các điểm z  thỏa mãn giả thiết đề bài là đường trung trực  của AB có phương trình ∆: x + 3y +10 = 0.
   Ta có |w| = |iz + 20| = |z – 20i| = CM với M là điểm biểu diễn số phức z và C(0; 20) .
   Do đó 
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====