Câu hỏi:
Số đỉnh của hình mười hai mặt đều là:
A.Mười sáu.
B.Mười hai.
C.Ba mươi.
D.Hai mươi.
Đáp án chính xác
Trả lời:
Đáp án D.
Hình mười hai mặt đều có 20 đỉnh.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
Biết giá trị lớn nhất và giá trị nhỏ nhất của hàm số lần lượt là \(M,m.\) Giá trị biểu thức \(P = {M^2} + {m^2}\) bằng
Câu hỏi:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
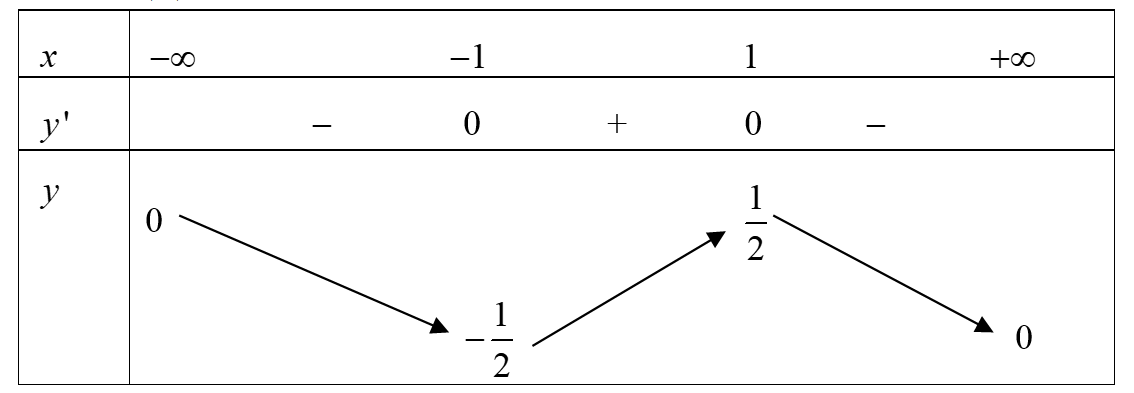
Biết giá trị lớn nhất và giá trị nhỏ nhất của hàm số lần lượt là \(M,m.\) Giá trị biểu thức \(P = {M^2} + {m^2}\) bằngA.\(P = \frac{1}{2}.\)
Đáp án chính xác
B.\(P = 1.\)
C.\(P = \frac{1}{4}.\)
D. \(P = 2.\)
Trả lời:
Đáp án A.
Từ bảng biến thiên, ta thấy \(M = \frac{1}{2},m = – \frac{1}{2}.\)
Vậy \(P = {M^2} + {m^2} = {\left( {\frac{1}{2}} \right)^2} + {\left( { – \frac{1}{2}} \right)^2} = \frac{1}{2}.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} = 2\) và công bội \(q = 2.\) Tính \({u_3}?\)
Câu hỏi:
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} = 2\) và công bội \(q = 2.\) Tính \({u_3}?\)
A.\({u_3} = 8.\)
Đáp án chính xác
B.\({u_3} = 4.\)
C.\({u_3} = 18.\)
D. \({u_3} = 6.\)
Trả lời:
Đáp án A.
Ta có: \({u_3} = {u_1}.{q^2} = {2.2^2} = 8.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu như sau:
Hàm số \(y = f\left( x \right)\) đồng biến trong khoảng nào dưới đây?
Câu hỏi:
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu như sau:

Hàm số \(y = f\left( x \right)\) đồng biến trong khoảng nào dưới đây?A.\(\left( { – 2;0} \right).\)
Đáp án chính xác
B.\(\left( {0; + \infty } \right).\)
C.\(\left( { – \infty ; – 2} \right).\)
D. \(\left( { – 3;1} \right).\)
Trả lời:
Đáp án A.
\(f’\left( x \right) >0\) với \(x \in \left( { – 2;0} \right)\) nên hàm số đồng biến trên khoảng \(\left( { – 2;0} \right).\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\) và hai mặt bên \(\left( {SAB} \right),\left( {SAC} \right)\) cùng vuông góc với mặt phẳng đáy. Tính thể tích của khối chóp \(S.ABC\) biết \(SC = a\sqrt 3 .\)
Câu hỏi:
Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\) và hai mặt bên \(\left( {SAB} \right),\left( {SAC} \right)\) cùng vuông góc với mặt phẳng đáy. Tính thể tích của khối chóp \(S.ABC\) biết \(SC = a\sqrt 3 .\)
A.\(\frac{{2{a^3}\sqrt 6 }}{9}.\)
B.\(\frac{{{a^3}\sqrt 6 }}{{12}}.\)
Đáp án chính xác
C.\(\frac{{{a^3}\sqrt 3 }}{4}.\)
D. \(\frac{{{a^3}\sqrt 3 }}{2}.\)
Trả lời:
Đáp án B.
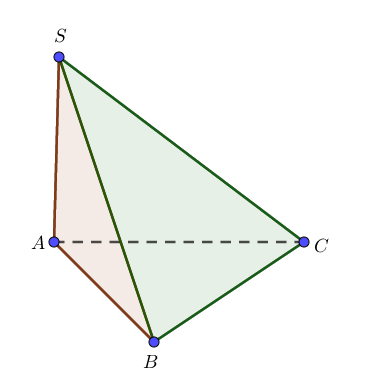
\(ABC\) là tam giác đều cạnh \(a\) nên \({S_{\Delta ABC}} = \frac{{{a^2}\sqrt 3 }}{4}.\)
Hai mặt bên \(\left( {SAB} \right),\left( {SAC} \right)\) cùng vuông góc với mặt đáy nên \(SA \bot \left( {ABC} \right).\)
Trong tam giác vuông \(SAC\) ta có: \(SA = \sqrt {S{C^2} – A{C^2}} = \sqrt {3{a^2} – {a^2}} = a\sqrt 2 .\)
Thể tích của khối chóp \(S.ABC\) là \(V = \frac{1}{3}{S_{\Delta ABC}}.SA = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{4}.a\sqrt 2 = \frac{{{a^3}\sqrt 6 }}{{12}}\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Kết luận nào sau đây về tính đơn điệu của hàm số \(y = \frac{{2x + 1}}{{x – 1}}\) là đúng?
Câu hỏi:
Kết luận nào sau đây về tính đơn điệu của hàm số \(y = \frac{{2x + 1}}{{x – 1}}\) là đúng?
A. Hàm số nghịch biến trên \(\mathbb{R}\backslash \left\{ 1 \right\}.\)
B. Hàm số đồng biến trên \(\mathbb{R}\backslash \left\{ 1 \right\}.\)
C. Hàm số nghịch biến trên \(\left( { – \infty ;1} \right)\) và \(\left( {1; + \infty } \right).\)
Đáp án chính xác
D. Hàm số đồng biến trên \(\left( { – \infty ;1} \right)\) và \(\left( {1; + \infty } \right).\)
Trả lời:
Đáp án C.
Tập xác định \(D = \mathbb{R}\backslash \left\{ 1 \right\}.\)
Ta có \(y’ = – \frac{3}{{{{\left( {x – 1} \right)}^2}}} < 0\) với mọi \(x \in D.\) Suy ra, hàm số nghịch biến trên \(\left( { – \infty ;1} \right)\) và \(\left( {1; + \infty } \right).\)====== **** mời các bạn xem câu tiếp bên dưới **** =====