Câu hỏi:
Một hình trụ có bán kính đáy và chiều cao đều bằng 4 dm. Một hình vuông ABCD có hai cạnh AB và CD lần lượt là các dây cung của hai đường tròn đáy. Biết mặt phẳng (ABCD) không vuông góc với mặt đáy của hình trụ. Tính diện tích S của hình vuông \(ABCD.\)
A. \(S = 20{\mkern 1mu} d{m^2}.\)
B. \(S = 40{\mkern 1mu} d{m^2}.\)
Đáp án chính xác
C. \(S = 80{\mkern 1mu} d{m^2}.\)
D. \(S = 60{\mkern 1mu} d{m^2}.\)
Trả lời:
Đáp án B
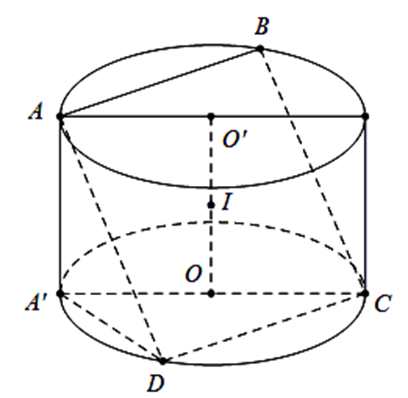
Gọi \(A’\) là hình chiếu của A trên mặt phẳng \(\left( O \right)\).
Ta có: \(A{\rm{D}} = \sqrt {A{{A’}^2} + A'{D^2}} = \sqrt {16 + A'{D^2}} \).
Tam giác \(A’DC\) vuông tại D nên
\(C{\rm{D}} = \sqrt {A'{C^2} – A'{D^2}} = \sqrt {{8^2} – A'{D^2}} \).
Do ABCD là hình vuông nên \(A{\rm{D}} = C{\rm{D}}\)
\( \Rightarrow \sqrt {16 + A'{D^2}} = \sqrt {64 – A'{D^2}} \Rightarrow 2{\rm{A’}}{D^2} = 48\).
Suy ra \(A'{D^2} = 24 \Rightarrow A{{\rm{D}}^2} = 40 = {S_{ABC{\rm{D}}}}\).
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian với hệ tọa độ \(Oxyz\), cho mặt phẳng \(\left( P \right):\frac{x}{3} + \frac{y}{2} + \frac{z}{1} = 1\). Vectơ nào dưới đây là vectơ pháp tuyến của \(\left( P \right)?\)
Câu hỏi:
Trong không gian với hệ tọa độ \(Oxyz\), cho mặt phẳng \(\left( P \right):\frac{x}{3} + \frac{y}{2} + \frac{z}{1} = 1\). Vectơ nào dưới đây là vectơ pháp tuyến của \(\left( P \right)?\)
A. \(\vec n = \left( {6;3;2} \right).\)
B. \(\vec n = \left( {2;3;6} \right).\)
Đáp án chính xác
C. \(\vec n = \left( {1;\frac{1}{2};\frac{1}{3}} \right).\)
D. \(\vec n = \left( {3;2;1} \right).\)
Trả lời:
Đáp án B
Mặt phẳng \(\left( P \right)\) có một VTPT là \(\overrightarrow {{n_1}} = \left( {\frac{1}{3};\frac{1}{2};\frac{1}{1}} \right) = \frac{1}{6}\left( {2;3;6} \right) = \frac{1}{6}\overrightarrow n \Rightarrow \overrightarrow n \) cũng là một VTPT của \(\left( P \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho \(a > 0,{\mkern 1mu} {\mkern 1mu} a \ne 1\) và \(x,y\) là hai số thực dương tùy ý. Khẳng định nào sau đây là khẳng định đúng?
Câu hỏi:
Cho \(a > 0,{\mkern 1mu} {\mkern 1mu} a \ne 1\) và \(x,y\) là hai số thực dương tùy ý. Khẳng định nào sau đây là khẳng định đúng?
A. \({\log _a}\left( {x – y} \right) = \frac{{{{\log }_a}x}}{{{{\log }_b}y}}.\)
B. \({\log _a}\frac{x}{y} = \frac{{{{\log }_a}x}}{{{{\log }_b}y}}.\)
C. \({\log _a}\frac{x}{y} = {\log _a}x – {\log _b}y.\)
Đáp án chính xác
D. \({\log _a}\left( {x – y} \right) = {\log _a}x – {\log _b}y.\)
Trả lời:
Đáp án C
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(y = f\left( x \right)\). Biết rằng hàm số f(x) có đạo hàm là \(f'\left( x \right)\) và hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ bên. Khẳng định nào sau đây sai?
Câu hỏi:
Cho hàm số \(y = f\left( x \right)\). Biết rằng hàm số f(x) có đạo hàm là \(f’\left( x \right)\) và hàm số \(y = f’\left( x \right)\) có đồ thị như hình vẽ bên. Khẳng định nào sau đây sai?
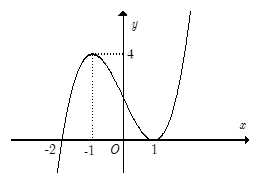
A. Hàmf(x) nghịch biến trên khoảng \(\left( { – \infty ; – 2} \right).\)
B. Hàm f(x) đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
C. Trên \(\left( { – 1;1} \right)\) thì hàm số f(x) luôn tăng.
D. Hàm f(x) giảm trên đoạn có độ dài bằng 2.
Đáp án chính xác
Trả lời:
Đáp án D
Dựa vào đồ thị hàm số \(y = f’\left( x \right)\) ta có bảng xét dấu \(f’\left( x \right)\).

Dựa vào bảng xét dấu ta thấy:
Hàm \(f\left( x \right)\) nghịch biến trên khoảng \(\left( { – \infty ; – 2} \right)\) suy ra A đúng.
Hàm \(f\left( x \right)\) đồng biến trên khoảng \(\left( {1; + \infty } \right)\) suy ra B đúng.
Trên \(\left( { – 1;1} \right)\) thì hàm số \(f\left( x \right)\) luôn tăng suy ra C đúng suy ra chọn D.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Phương trình \({4^{2x + 1}} = 32\) có nghiệm là
Câu hỏi:
Phương trình \({4^{2x + 1}} = 32\) có nghiệm là
A. \(x = \frac{5}{2}.\)
B. \(x = \frac{5}{4}.\)
C. \(x = \frac{3}{4}.\)
Đáp án chính xác
D. \(x = 1.\)
Trả lời:
Đáp án C
Ta có: \({4^{2{\rm{x}} + 1}} = 32 \Leftrightarrow {2^{2\left( {2{\rm{x}} + 1} \right)}} = {2^5} \Leftrightarrow 4{\rm{x}} + 2 = 5 \Leftrightarrow x = \frac{3}{4}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho cấp số cộng \({u_n}\) có các số hạng đầu lần lượt là 5; 9; 13; 17;…Tìm số hạng tổng quát \({u_n}\) của cấp số cộng?
Câu hỏi:
Cho cấp số cộng \({u_n}\) có các số hạng đầu lần lượt là 5; 9; 13; 17;…Tìm số hạng tổng quát \({u_n}\) của cấp số cộng?
A. \({u_n} = 4n + 1.\)
Đáp án chính xác
B. \({u_n} = 5n – 1.\)
C. \({u_n} = 5n + 1.\)
D. \({u_n} = 4n – 1.\)
Trả lời:
Đáp án A
Dãy số đã cho là cấp số cộng có \({u_1} = 5;{u_2} = 9 \Rightarrow d = {u_2} – {u_1} = 9 – 5 = 4\).
Do đó \({u_n} = {u_1} + \left( {n – 1} \right)d = 5 + 4\left( {n – 1} \right) = 4n + 1\).
Vậy \({u_n} = 4n + 1\).====== **** mời các bạn xem câu tiếp bên dưới **** =====