Câu hỏi:
Kí hiệu a, A lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y = \frac{{{x^2} + x + 4}}{{x + 1}}\) trên đoạn \(\left[ {0;2} \right]\). Giá trị của \(a + A\) bằng
A. \(\frac{{19}}{3}\)
B. \(\frac{{22}}{3}\)
C. 7
Đáp án chính xác
D. 12
Trả lời:
Đáp án C
+ \(y’ = \frac{{\left( {2{\rm{x}} + 1} \right)\left( {x + 1} \right) – \left( {{x^2} + x + 4} \right)}}{{{{\left( {x + 1} \right)}^2}}} = \frac{{{x^2} + 2{\rm{x}} – 3}}{{{{\left( {x + 1} \right)}^2}}}\).
+ \(y’ = 0 \Leftrightarrow {x^2} + 2{\rm{x}} – 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 \in \left( {0;2} \right)\\x = – 3 \notin \left( {0;2} \right)\end{array} \right.\).
+ \(y\left( 0 \right) = 4,{\rm{ y}}\left( 2 \right) = \frac{{10}}{3},{\rm{ y}}\left( 1 \right) = 3\).
Khi đó, \(a = \mathop {\min }\limits_{\left[ {0;2} \right]} y = 3,{\rm{ }}A = \mathop {\max }\limits_{\left[ {0;2} \right]} y = 4\). Vậy \(a + A = 7\).
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho 10 điểm phân biệt trong đó không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác mà ba đỉnh của nó được chọn từ 10 điểm trên?
Câu hỏi:
Cho 10 điểm phân biệt trong đó không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác mà ba đỉnh của nó được chọn từ 10 điểm trên?
A. \(C_{10}^3\)
B. \(A_{10}^3\)
C. \(C_{10}^3 – 10\)
Đáp án chính xác
D. \({10^3}\)
Trả lời:
Đáp án A
Chọn 3 điểm từ 10 điểm phân biệt trong đó không có 3 điểm nào thẳng hàng ta được một tam giác suy ra có \(C_{10}^3\) tam giác dược tạo thành.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian với hệ tọa độ Oxyz cho điểm \(A\left( {1; – 1;2} \right)\) và mặt phẳng \(\left( P \right):2{\rm{x}} – y + z + 1 = 0\). Mặt phẳng \(\left( Q \right)\) đi qua điểm A và song song với \(\left( P \right)\). Phương trình mặt phẳng \(\left( Q \right)\) là
Câu hỏi:
Trong không gian với hệ tọa độ Oxyz cho điểm \(A\left( {1; – 1;2} \right)\) và mặt phẳng \(\left( P \right):2{\rm{x}} – y + z + 1 = 0\). Mặt phẳng \(\left( Q \right)\) đi qua điểm A và song song với \(\left( P \right)\). Phương trình mặt phẳng \(\left( Q \right)\) là
A. \(2{\rm{x}} – y + z – 5 = 0\)
Đáp án chính xác
B. \(2{\rm{x}} – y + z = 0\)
C. \(x + y + z – 2 = 0\)
D. \(2{\rm{x}} + y – z + 1 = 0\)
Trả lời:
Đáp án A
Do \(\left( Q \right)\) song song với \(\left( P \right)\) nên phương trình của \(\left( Q \right)\) có dạng \(2{\rm{x}} – y + z + a = 0\) với \(a \ne 1\).
Do \(\left( Q \right)\) đi qua điểm A nên \(2.1 + 1 + 2 + a = 0 \Leftrightarrow a = – 5\).
Vậy phương trình \(\left( Q \right):2{\rm{x}} – y + z – 5 = 0\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Số nghiệm nguyên của bất phương trình \({\log _{\frac{1}{2}}}\left( {x – 3} \right) \ge {\log _{\frac{1}{2}}}4\) là
Câu hỏi:
Số nghiệm nguyên của bất phương trình \({\log _{\frac{1}{2}}}\left( {x – 3} \right) \ge {\log _{\frac{1}{2}}}4\) là
A. 5
B. 6
C. 3
D. 4
Đáp án chính xác
Trả lời:
Đáp án D
Ta có: BPT . Do đó có 4 giá trị nguyên thỏa mãn.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng \(\sqrt 2 a\). Độ lớn của góc giữa đường thẳng SA và mặt phẳng đáy bằng
Câu hỏi:
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng \(\sqrt 2 a\). Độ lớn của góc giữa đường thẳng SA và mặt phẳng đáy bằng
A. \(45^\circ \)
B. \(75^\circ \)
C. \(30^\circ \)
D. \(60^\circ \)
Đáp án chính xác
Trả lời:
Đáp án D
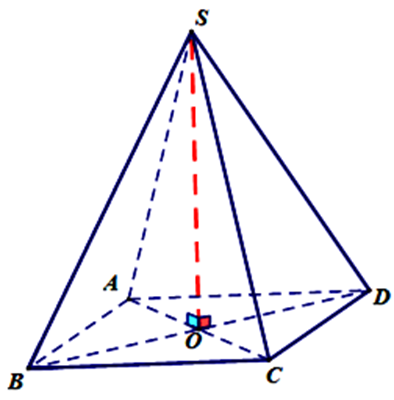
Gọi O là tâm hình vuông.
Suy ra AO là hình chiếu vuông góc của SA lên mặt phẳng \(\left( {ABC{\rm{D}}} \right)\).
Vậy góc giữa đường thẳng SA và mặt phẳng \(\left( {ABC{\rm{D}}} \right)\) là \(\widehat {SAO}\).
Tam giác SAO vuông tại O có
\(\cos \widehat {SAO} = \frac{{AO}}{{SA}} = \frac{{\frac{{a\sqrt 2 }}{2}}}{{a\sqrt 2 }} = \frac{1}{2} \Rightarrow \widehat {SAO} = 60^\circ \).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong hình vẽ bên điểm M biểu diễn số phức \({z_1}\), điểm N biểu diễn số phức \({z_2}\). Hỏi trung điểm của đoạn MN là điểm biểu diễn hình học của số phức nào sau đây
Câu hỏi:
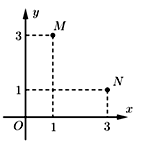
Trong hình vẽ bên điểm M biểu diễn số phức \({z_1}\), điểm N biểu diễn số phức \({z_2}\). Hỏi trung điểm của đoạn MN là điểm biểu diễn hình học của số phức nào sau đây
A. \(z = 1 + i\)
B. \(z = 2 + 2i\)
Đáp án chính xác
C. \(z = 4 + 4i\)
D. \(z = 2 – 2i\)
Trả lời:
Đáp án B
Điểm \(M\left( {1;3} \right),N\left( {3;1} \right)\) nên trung điểm của MN là \(I\left( {2;2} \right)\).
Vậy \(z = 2 + 2i\).====== **** mời các bạn xem câu tiếp bên dưới **** =====