Câu hỏi:
Kết quả nguyên hàm \(I = \int {\left( {4x – 1} \right).{{\ln }^3}\left( {2x} \right)dx} \) là:
A. \(\left( {2{x^2} – x} \right){\ln ^3}\left( {2x} \right) – \left( {3{x^2} – 3x} \right){\ln ^2}\left( {2x} \right) – \left( {3{x^2} – 6x} \right)\ln \left( {2x} \right) + \frac{{3{x^2}}}{2} + 6x + C\)
B. \(\left( {2{x^2} – x} \right){\ln ^3}\left( {2x} \right) – \left( {3{x^2} – 3x} \right){\ln ^2}\left( {2x} \right) + \left( {3{x^2} – 6x} \right)\ln \left( {2x} \right) – \frac{{3{x^2}}}{2} + 6x + C\)
Đáp án chính xác
C. \(\left( {2{x^2} – x} \right){\ln ^3}\left( {2x} \right) + \left( {3{x^2} – 3x} \right){\ln ^2}\left( {2x} \right) + \left( {3{x^2} – 6x} \right)\ln \left( {2x} \right) – \frac{{3{x^2}}}{2} + 6x + C\)
D. \(\left( {2{x^2} – x} \right){\ln ^3}\left( {2x} \right) + \left( {3{x^2} – 3x} \right){\ln ^2}\left( {2x} \right) + \left( {3{x^2} – 6x} \right)\ln \left( {2x} \right) – \frac{{3{x^2}}}{2} – 6x + C\)
Trả lời:
Hướng dẫn giải
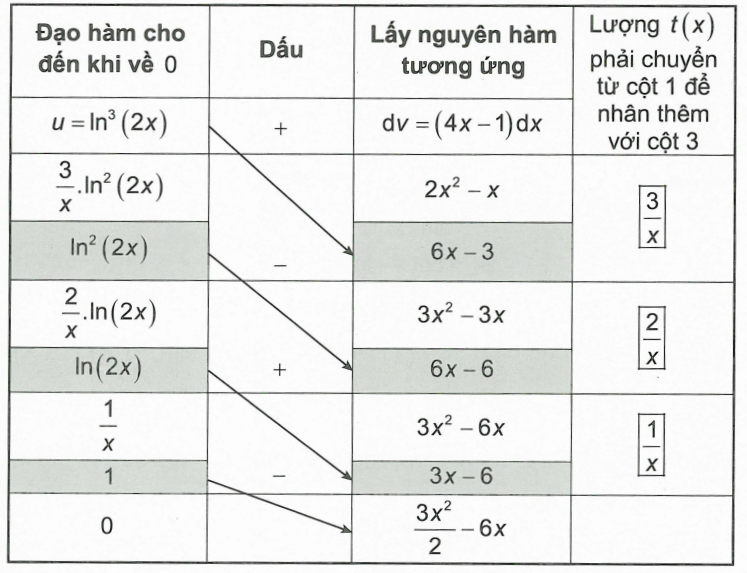
Vậy \(I = \left( {2{x^2} – x} \right){\ln ^3}\left( {2x} \right) – \left( {3{x^2} – 3x} \right){\ln ^2}\left( {2x} \right) + \left( {3{x^2} – 6x} \right)\ln \left( {2x} \right) – \frac{{3{x^2}}}{2} + 6x + C\)
Chọn B.
====== **** mời các bạn xem câu tiếp bên dưới **** =====