Hàm số y=f(x) có f(-2)=f(2)=0 và y=f'(x) như hình vẽ. Hàm số gx=f3−x2  nghịch biến trên khoảng nào?

Câu hỏi:

Hàm số y=f(x) có f(-2)=f(2)=0 và y=f'(x) như hình vẽ. Hàm số $g\left(x\right)={\left[f\left(3-x\right)\right]}^2$  nghịch biến trên khoảng nào?

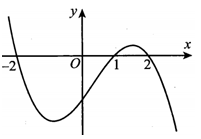
A. $\left(-2;2\right).$

B. $\left(1;2\right).$

C. $\left(2;5\right).$

Đáp án chính xác

D. $\left(5;+\infty \right).$

Trả lời:

Đáp án C
Ta có $g‘\left(x\right)=-2f\left(3-x\right)f‘\left(3-x\right)$ .
Lập bảng biến thiên của hàm số $y=f\left(x\right)$  như sau

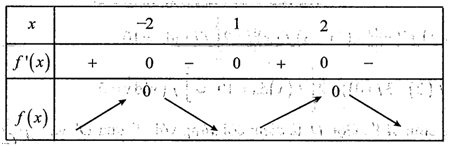
Khi đó ta thấy rằng phương trình $f\left(x\right)=0$  có nghiệm kép không được chọn và bản thân phương trình $f\left(3-x\right)=0$  cũng thế.

Do vậy $f‘\left(3-x\right)=0\iff \left[\begin{array}{l}3-x=-2\\ 3-x=1\\ 3-x=2\end{array}\right.\iff \left[\begin{array}{l}x=5\\ x=2\\ x=1\end{array}\right..$
Lập trục xét dấu:

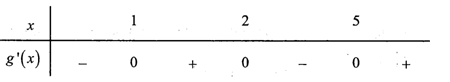
Từ trục xét dấu, suy ra hàm số g(x) nghịch biến trên các khoảng $\left(-\infty ;1\right)$  và $\left(2;5\right)$ .

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Hàm số y=log73x+1  có tập xác định là:
   
   

   Câu hỏi:
   

   Hàm số $y={\log }_7\left(3x+1\right)$  có tập xác định là:

   A. $\left(-\frac{1}{3};+\infty \right).$

   Đáp án chính xác

   B. $\left(-\infty ;-\frac{1}{3}\right).$

   C. $\left(0;+\infty \right).$

   D. $\left[-\frac{1}{3};+\infty \right).$

   Trả lời:

   Đáp án A
   Hàm số xác định khi $3x+1>0\iff x>-\frac{1}{3}$ . Tập xác định: $D=\left(-\frac{1}{3};+\infty \right)$ .

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Trong A, B lần lượt là diểm biểu diễn các số phứcz1,z2. Trọng tâm G của tam giác OAB là điểm biểu diễn số phức như trong hình vẽ. Giá trị z12+z22+z32   bằng:
   
   

   Câu hỏi:
   

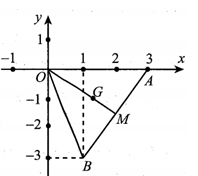
   Trong A, B lần lượt là diểm biểu diễn các số phức$z_1,z_2$. Trọng tâm G của tam giác OAB là điểm biểu diễn số phức như trong hình vẽ. Giá trị ${\left|z_1\right|}^2+{\left|z_2\right|}^2+{\left|z_3\right|}^2$   bằng:

   

   A.$\frac{79}{9}.$

   B.$\frac{196}{9}.$

   Đáp án chính xác

   C.$\frac{49}{4}.$

   D.$\frac{97}{4}.$

   Trả lời:

   Đáp án B
   Ta có:$A\left(3;0\right),B\left(1;-3\right)\Rightarrow G\left(\frac{4}{3};-1\right)$ .
   Suy ra ${\left|z_1\right|}^2+{\left|z_2\right|}^2+{\left|z_3\right|}^2=O{A}^2+O{B}^2+O{G}^2=3^2+1^2+{\left(-3\right)}^2+{\left(\frac{4}{3}\right)}^2+{\left(-1\right)}^2=\frac{196}{9}$ .

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho hàm số y=f(x) có bảng biến thiên như sau: Số điểm cực đại của hàm số đã cho bằng:
   
   

   Câu hỏi:
   

   Cho hàm số y=f(x) có bảng biến thiên như sau:
   

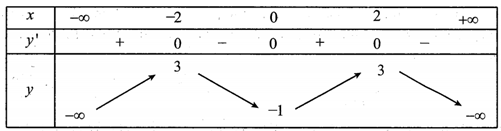
   Số điểm cực đại của hàm số đã cho bằng:

   A.1

   B.2

   Đáp án chính xác

   C.3

   D.0

   Trả lời:

   Đáp án B
   Hàm số đạt cực đại tại các điểm $x=\pm 2$ .
   Vậy số điểm cực đại của hàm số đã cho bằng 2.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho F(x) là một nguyên hàm của f(x) trên [0;1], biết F1=2  và ∫−11x+1Fxdx=1 . Giá trị tích phân S=∫−11x+12fxdx  là:
   
   

   Câu hỏi:
   

   Cho F(x) là một nguyên hàm của f(x) trên [0;1], biết $F\left(1\right)=2$  và $\underset{-1}{\overset{1}{\int }}\left(x+1\right)F\left(x\right)dx=1$ . Giá trị tích phân $S=\underset{-1}{\overset{1}{\int }}{\left(x+1\right)}^{2}f\left(x\right)dx$  là:

   A. S=6

   Đáp án chính xác

   B.S=3

   C.S=2

   D. S=9

   Trả lời:

   Đáp án A
   Ta có: $S=\underset{-1}{\overset{1}{\int }}{\left(x+1\right)}^{2}f\left(x\right)dx=\underset{-1}{\overset{1}{\int }}{\left(x+1\right)}^{2}dF\left(x\right)=F\left(x\right){\left(x+1\right)}^2\left|{}_{-1}^1\right.-2\underset{-1}{\overset{1}{\int }}\left(x+1\right)F\left(x\right)dx=6$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hàm số y=f(x) có bảng biến thiên như sau: Đồ thị hàm số y=1f2020−x−2  có bao nhiêu tiệm cận đứng?
   
   

   Câu hỏi:
   

   Cho hàm số y=f(x) có bảng biến thiên như sau:
   

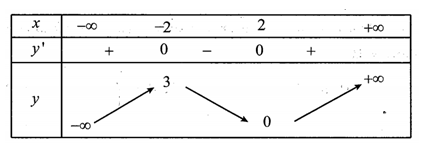
   Đồ thị hàm số $y=\frac{1}{f\left(2020-x\right)-2}$  có bao nhiêu tiệm cận đứng?

   A.2

   B.3

   Đáp án chính xác

   C.1

   D.0

   Trả lời:

   Đáp án B
   Dựa vào bảng biến thiên, ta có $f\left(x\right)=2$  có 3 nghiệm.
   Suy ra đồ thị hàm số$y=\frac{1}{f\left(2020-x\right)-2}$  có 3 tiệm cận đứng.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====