Hàm số y = x8 + (x4 – 1) 2 + 5  đạt giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [0;2]  lần lượt tại hai điểm có hoành độ x1; x2. Khi đó tích x1.x2  có giá trị bằng:

Câu hỏi:

Hàm số y = x⁸ + (x⁴ – 1) ² + 5  đạt giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [0;2]  lần lượt tại hai điểm có hoành độ x₁; x₂. Khi đó tích x₁.x₂  có giá trị bằng:

A. 1.

B. 2.

C. 3/2.

D. 0.

Đáp án chính xác

Trả lời:

Đặt  t= x⁴– 1( -1≤ t≤ 15).
Khi đó hàm số trở thành:  y= ( t+1) ²+ t²+ 5=2t²+ 2t+6
Đạo hàm y’ = 4t+ 2> 0 mọi x thòa mãn 0≤ x≤ 2
Hàm số đồng biến trên đoạn [0; 2].
 Hàm số đạt giá trị lớn nhất tại x= 2 tức là t= 15, hàm số đạt giá trị nhỏ nhất tại x= 0 hay t=1
Chọn D.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Tìm tất các giá trị thực của tham số m  để hàm số y=13×3+(m+3)x2+4(m+3)x+m3-m đạt cực trị tại x1,x2 thỏa mãn -2<x1<x2
   
   

   Câu hỏi:
   

   Tìm tất các giá trị thực của tham số m  để hàm số $y=\frac{1}{3}{x}^3+(m+3)x^2+4(m+3)x+m^3–m$ đạt cực trị tại $x_1,x_2$ thỏa mãn -2<$x_1<x_2$

   A. m< -2.

   B. m< 1.

   C. m< -3

   Đáp án chính xác

   D. m>3

   Trả lời:

   + Ta có: y’ = x² + 2(m+3)x + 4(m+3) 
   Yêu cầu của bài toán tường đương y’ =0 có hai nghiệm phân biệt x₁; x₂  thỏa mãn: -2 < x₁< x₂ 
   
   
   
   Chọn C

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Tìm các giá trị của tham số m để hàm số: y=13mx3-(m-1)x2+3m-2x+16 đạt cực trị tại x1&lt;x2 thỏa mãn 4×1+3×2=3
   
   

   Câu hỏi:
   

   Tìm các giá trị của tham số m để hàm số: $y=\frac{1}{3}m{x}^3–(m–1)x^2+3\left(m–2\right)x+\frac{1}{6}$
   đạt cực trị tại $x_1<x_{2 }thỏa mãn 4x_1+3x_2=3$

   A. $1–\frac{\sqrt{6}}{2}<m<1+\frac{\sqrt{6}}{2}$

   B. 1<m<2

   C. 2< m<3

   D. Đáp án khác

   Đáp án chính xác

   Trả lời:

   Ta có: y’ = $m{x}^2–2(m–1)x+3(m–2)$
   Yêu cầu của bài toán tương đương y’ = 0  có hai nghiệm phân biệt  $x_1;x_2 thỏa mãn 4x_1+3x_2=3$   
   
   
   
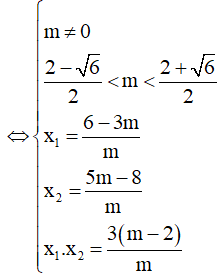
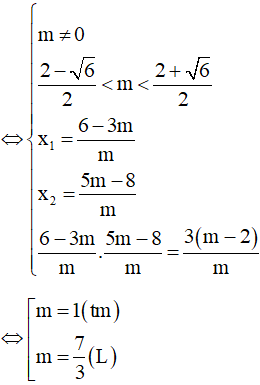
   Chọn D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho hàm số y= f(x) =ax3+ bx2+cx+d  có đạo hàm là hàm số y= f’ (x)  với đồ thị như hình vẽ bên. Biết rằng đồ thị hàm số y= f( x)  tiếp xúc với trục hoành tại điểm có hoành độ dương . Khi đó đồ thị hàm số y= f( x)  cắt trục tung tại điểm có tung độ là bao nhiêu?
   
   

   Câu hỏi:
   

   Cho hàm số y= f(x) =ax³+ bx²+cx+d  có đạo hàm là hàm số y= f’ (x)  với đồ thị như hình vẽ bên. Biết rằng đồ thị hàm số y= f( x)  tiếp xúc với trục hoành tại điểm có hoành độ dương . Khi đó đồ thị hàm số y= f( x)  cắt trục tung tại điểm có tung độ là bao nhiêu?
   

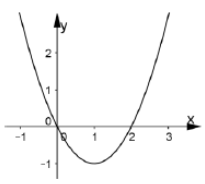
   A. 2/3

   B. 1

   C. 3/2

   D. 4/3

   Đáp án chính xác

   Trả lời:

   + Ta có đạo hàm f’(x) = 3ax²+ 2bx+c .
   + Dựa vào đồ thị hàm số y = f’(x) ta thấy đồ thị hàm số  đi qua các điểm (0; 0); (1; -1); (2; 0) nên  a = 1/3; b = -1; c = 0.
   Do vậy hàm số cần tìm có dạng y = 1/3 x³-x²+ d  .
    Điểm tiếp xúc với trục hoành là cực trị của đồ thị hàm số và tại đó ta có x = 0 hoặc x = 2.
   + Vì đồ thị hàm số y = f(x)  tiếp xúc với trục hoành tại điểm có hoành độ dương nên đồ thị hàm số tiếp xúc trục hoành tại điểm  x = 2 nghĩa là:
    f(2) = 0 hay  8/3 – 4 + d= 0  nên d = 4/3
   Chọn D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Giá trị lớn nhất của hàm số y=x+4+4-x-4x+44-x+5  bằng
   
   

   Câu hỏi:
   

   Giá trị lớn nhất của hàm số $y=\sqrt{x+4}+\sqrt{4–x}–4\sqrt{\left(x+4\right)\left(4–x\right)}+5$  bằng

   A. $\underset{[–4;4]}{max}y=10$

   B. $\underset{[–4;4]}{max}y=5–2\sqrt{2}$

   C. $\underset{[–4;4]}{max}y=–7$

   D. $\underset{[–4;4]}{max}y=5+2\sqrt{2}$

   Đáp án chính xác

   Trả lời:

   Chọn D.+) Điều kiện: -4 ≤ x ≤ 4. Ta  thấy  hàm số f(x) liên tục trên đoạn [ -4; 4]đặt t = 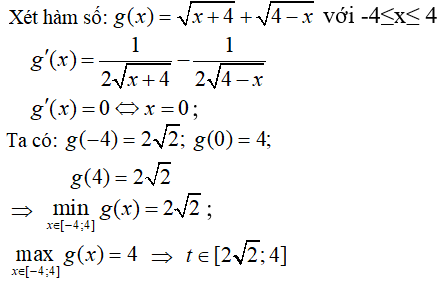$\sqrt{x+4}+\sqrt{4–x}$$\Rightarrow t^2=x+4+4–x+2\sqrt{(x+4)(4–x)}$$\Rightarrow \sqrt{(x+4)(4–x)} =\frac{t^2–8}{2}$Ta có: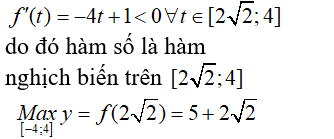

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hàm số y= 2×3-3×2+1  có đồ thị và đường thẳng  d: y=x-1. Giao điểm của (C)  và d  lần lượt là A( 1; 0); B và C. Khi đó khoảng cách giữa B và C  là
   
   

   Câu hỏi:
   

   Cho hàm số y= 2x³-3x²+1  có đồ thị và đường thẳng  d: y=x-1. Giao điểm của (C)  và d  lần lượt là A( 1; 0); B và C. Khi đó khoảng cách giữa B và C  là

   A. BC=$\frac{\sqrt{30}}{2}$

   B.  BC=$\frac{\sqrt{34}}{2}$

   Đáp án chính xác

   C.  BC=$\frac{3\sqrt{2}}{2}$

   D.  BC=$\frac{\sqrt{14}}{2}$

   Trả lời:

    
   2x³-3x²+1  =x-1 hay 2x³-3x²-x+2=0
   
   
   Khi đó ta có A(1 ; 0) ; B( x₁ ; x₁-1) và C( x₂ ; x₂-1)   ( x₁ ; x₂ là  nghiệm của (1))
   Ta có , suy ra
   
   
   
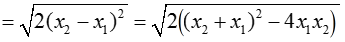
   Chọn B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====