Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y=2mx+m−2x+1  cắt đường thẳng d:y=x+3  tại hai điểm phân biệt A, B sao cho tam giác IAB có diện tích bằng 3, với I−1;1 . Tổng tất cả các phần tử của S bằng

Câu hỏi:

Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số $y=\frac{2m\text{x}+m-2}{x+1}$  cắt đường thẳng $\left(d\right):y=x+3$  tại hai điểm phân biệt A, B sao cho tam giác IAB có diện tích bằng 3, với $I\left(-1;1\right)$ . Tổng tất cả các phần tử của S bằng

A. $\frac{7}{2}$

B. -10

C. 3

Đáp án chính xác

D. 5

Trả lời:

Phương trình hoành độ giao điểm $\frac{2m\text{x}+m-2}{x+1}=x+3\iff f\left(x\right)=x^2+\left(4-2m\right)x+5-m=0$  ( $x\ne -1$). Đồ thị (C) của hàm số $y=\frac{2m\text{x}+m-2}{x+1}$  cắt đường thẳng $\left(d\right):y=x+3$  tại hai điểm phân biệt khi và chỉ khi $\left\{\begin{array}{l}{\Delta }^{‘}>0\\ f\left(-1\right)\ne 0\end{array}\right.\iff \left\{\begin{array}{l}{m}^2-3m-1>0\\ m\ne -2\end{array}\right.$(*). (C) cắt d tại A, B suy ra $x_A,x_B$  là nghiệm của phương trình
f(x) = 0
, theo định lí Vi-ét ta có $\left\{\begin{array}{l}{x}_A+x_B=2m-4\\ x_A{x}_B=5-m\end{array}\right.$ .
$A\left(x_A;x_A+3\right),B\left(x_B;x_B+3\right)$ suy ra $AB=\sqrt{2{\left(x_A-x_B\right)}^2}=\sqrt{2{\left(x_A+x_B\right)}^2-8{\text{x}}_A{x}_B}=\sqrt{8m^2-24m-8}$ .
Ta có $AB=\sqrt{2{\left(x_A-x_B\right)}^2}=\sqrt{2{\left(x_A+x_B\right)}^2-8{\text{x}}_A{x}_B}=\sqrt{8m^2-24m-8}$  (thỏa mãn *).
Suy ra tổng các phần tử của S là 3.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Hàm số y=log73x+1  có tập xác định là:
   
   

   Câu hỏi:
   

   Hàm số $y={\log }_7\left(3x+1\right)$  có tập xác định là:

   A. $\left(-\frac{1}{3};+\infty \right).$

   Đáp án chính xác

   B. $\left(-\infty ;-\frac{1}{3}\right).$

   C. $\left(0;+\infty \right).$

   D. $\left[-\frac{1}{3};+\infty \right).$

   Trả lời:

   Đáp án A
   Hàm số xác định khi $3x+1>0\iff x>-\frac{1}{3}$ . Tập xác định: $D=\left(-\frac{1}{3};+\infty \right)$ .

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Trong A, B lần lượt là diểm biểu diễn các số phức . Trọng tâm G của tam giác OAB là điểm biểu diễn số phức như trong hình vẽ. Giá trị z12+z22+z32  bằng:
   
   

   Câu hỏi:
   

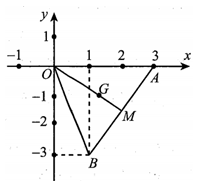
   Trong A, B lần lượt là diểm biểu diễn các số phức . Trọng tâm G của tam giác OAB là điểm biểu diễn số phức như trong hình vẽ. Giá trị ${\left|z_1\right|}^2+{\left|z_2\right|}^2+{\left|z_3\right|}^2$  bằng:
   

   A. $\frac{79}{9}.$

   B. $\frac{196}{9}.$

   Đáp án chính xác

   C. $\frac{49}{4}.$

   D. $\frac{97}{4}.$

   Trả lời:

   Đáp án B
   Ta có: $A\left(3;0\right),B\left(1;-3\right)\Rightarrow G\left(\frac{4}{3};-1\right)$ .
   Suy ra ${\left|z_1\right|}^2+{\left|z_2\right|}^2+{\left|z_3\right|}^2=O{A}^2+O{B}^2+O{G}^2=3^2+1^2+{\left(-3\right)}^2+{\left(\frac{4}{3}\right)}^2+{\left(-1\right)}^2=\frac{196}{9}$ .

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho hàm số y=fx  có bảng biến thiên như sau: Số điểm cực đại của hàm số đã cho bằng:
   
   

   Câu hỏi:
   

   Cho hàm số $y=f\left(x\right)$  có bảng biến thiên như sau:
   

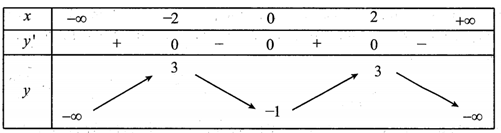
   Số điểm cực đại của hàm số đã cho bằng:

   A. 1

   B. 2

   Đáp án chính xác

   C. 3

   D. 0

   Trả lời:

   Đáp án B
   Hàm số đạt cực đại tại các điểm $x=\pm 2$ .
   Vậy số điểm cực đại của hàm số đã cho bằng 2.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho F(x) là một nguyên hàm của f(x) trên [0;1]  , biết F1=2  và ∫−11x+1Fxdx=1 . Giá trị tích phân S=∫−11x+12fxdx  là:
   
   

   Câu hỏi:
   

   Cho F(x) là một nguyên hàm của f(x) trên [0;1]  , biết $F\left(1\right)=2$  và $\underset{-1}{\overset{1}{\int }}\left(x+1\right)F\left(x\right)dx=1$ . Giá trị tích phân $S=\underset{-1}{\overset{1}{\int }}{\left(x+1\right)}^{2}f\left(x\right)dx$  là:

   A. $S=6.$

   Đáp án chính xác

   B. $S=3.$

   C. $S=2$

   D. $S=9.$

   Trả lời:

   Đáp án A
   Ta có: $S=\underset{-1}{\overset{1}{\int }}{\left(x+1\right)}^{2}f\left(x\right)dx=\underset{-1}{\overset{1}{\int }}{\left(x+1\right)}^{2}dF\left(x\right)=F\left(x\right){\left(x+1\right)}^2\left|{}_{-1}^1\right.-2\underset{-1}{\overset{1}{\int }}\left(x+1\right)F\left(x\right)dx=6$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hàm số y=f(x) có bảng biến thiên như sau: Đồ thị hàm số y=1f2020−x−2  có bao nhiêu tiệm cận đứng?
   
   

   Câu hỏi:
   

   Cho hàm số y=f(x) có bảng biến thiên như sau:
   

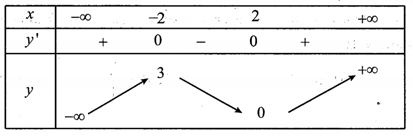
   Đồ thị hàm số $y=\frac{1}{f\left(2020-x\right)-2}$  có bao nhiêu tiệm cận đứng?

   A. 2

   B. 3

   Đáp án chính xác

   C. 1

   D. 0

   Trả lời:

   Đáp án B
   Dựa vào bảng biến thiên, ta có$f\left(x\right)=2$  có 3 nghiệm.
   Suy ra đồ thị hàm số $y=\frac{1}{f\left(2020-x\right)-2}$  có 3 tiệm cận đứng

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====