Câu hỏi:
Diện tích phần gạch chéo trong hình dưới bằng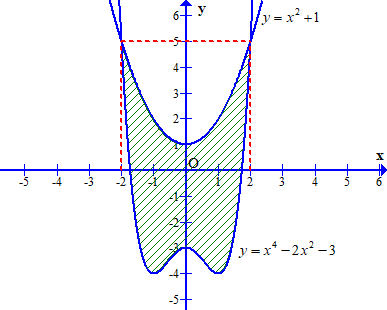
A.\(\int\limits_{ – 2}^2 {\left( {{x^4} – 2{x^2} – 3} \right){\rm{d}}x} \).
B.\(\int\limits_{ – 2}^2 {\left( {{x^4} – 3{x^2} – 4} \right){\rm{d}}x} \).
C.\(\int\limits_{ – 2}^2 {\left( {{x^4} + 3{x^2} – 4} \right){\rm{d}}x} \).
D.\(\int\limits_{ – 2}^2 {\left( { – {x^4} + 3{x^2} + 4} \right){\rm{d}}x} \).
Đáp án chính xác
Trả lời:
Ta có \(S = \int\limits_{ – 2}^2 {\left[ {{x^2} + 1 – \left( {{x^4} – 2{x^2} – 3} \right)} \right]{\rm{d}}x} = \int\limits_{ – 2}^2 {\left( { – {x^4} + 3{x^2} + 4} \right){\rm{d}}x} \).Chọn đáp án D
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trên giá sách có \(10\) quyển sách tiếng Việt khác nhau, \(8\) quyển sách Toán khác nhau. Hỏi có bao nhiêu cách chọn một quyển sách?
Câu hỏi:
Trên giá sách có \(10\) quyển sách tiếng Việt khác nhau, \(8\) quyển sách Toán khác nhau. Hỏi có bao nhiêu cách chọn một quyển sách?
A.\(10\).
B. \(8\).
C.\(80\).
D.\(18\).
Đáp án chính xác
Trả lời:
Theo quy tắc cộng, ta có số cách chọn ra một quyển sách từ \(10\) quyển sách tiếng Việt khác nhau và \(8\) quyển sách Toán khác nhau là \(10 + 8 = 18\) cách chọn.
Chọn đáp án D====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 2\) và công bội \(q = 3\). Tính \({u_3}\).
Câu hỏi:
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 2\) và công bội \(q = 3\). Tính \({u_3}\).
A.\(54\).
B. \(6\).
C.\(18\).
Đáp án chính xác
D.\(12\).
Trả lời:
Áp dụng công thức \({u_n} = {u_1}.{q^{n – 1}}\) ta có \({u_3} = {u_1}.{q^2} = {2.3^2} = 18\).
Chọn đáp án C====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Diện tích toàn phần của một hình nón có độ dài đường sinh \(l\) gấp đôi bán kính đáy \(r\) là
Câu hỏi:
Diện tích toàn phần của một hình nón có độ dài đường sinh \(l\) gấp đôi bán kính đáy \(r\) là
A.\(\frac{3}{4}\pi {l^2}\).
Đáp án chính xác
B.\(2\pi r{l^2}\).
C.\(4\pi {r^2}\).
D.\(\frac{3}{4}{\pi ^2}l\).
Trả lời:
Diện tích toàn phần của khối nón có độ dài đường sinh \(l\) gấp đôi bán kính đáy \(r\)là \({S_{tp}} = \pi rl + \pi {r^2} = \pi \frac{l}{2}l + \pi {\left( {\frac{l}{2}} \right)^2} = \frac{3}{4}\pi {l^2}\).
Chọn đáp án A====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ bên dưới.
Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
Câu hỏi:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ bên dưới.
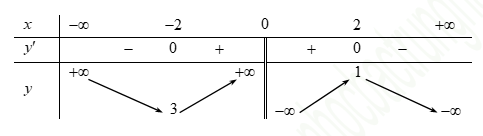
Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?A.\(\left( { – 2;\,2} \right)\).
B.\(\left( {0;\,2} \right)\).
Đáp án chính xác
C.\(\left( {3;\, + \infty } \right)\).
D.\(\left( { – \infty ;\,1} \right)\).
Trả lời:
Hàm số xác định trên khoảng \(\left( { – \infty ;\,0} \right) \cup \left( {0;\, + \infty } \right)\) và có đạo hàm \(y’ >0\) với \(x \in \left( { – 2;\,0} \right) \cup \left( {0;\,2} \right)\).
\( \Rightarrow \) hàm số đồng biến trên khoảng \(\left( {0;\,2} \right)\).* Nhận xét: Câu 4 trong đề minh hoạ 2020 là câu mức độ nhận biết thuộc kiến thức Chương 1 Giải tích 12 – bài 1: Sự đồng biến, nghịch biến của hàm số. Học sinh nắm rõ lý thuyết “ Sự biến thiên và dấu của đạo h àm” là làm được.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho khối lập phương \(ABCD.A'B'C'D'\) có diện tích toàn phần bằng 54 . Thể tích của khối lập phương đã cho bằng
Câu hỏi:
Cho khối lập phương \(ABCD.A’B’C’D’\) có diện tích toàn phần bằng 54 . Thể tích của khối lập phương đã cho bằng
A. 9.
B. 27.
Đáp án chính xác
C. 3.
D. 81.
Trả lời:
Diện tích một mặt của hình lập phương bằng \(\frac{{54}}{6} = 9\).
Suy ra độ dài một cạnh của hình lập phương bằng \(\sqrt 9 = 3\).
Vậy thể tích của khối lập phương là \(V = {3^3} = 27\).
Chọn đáp án B====== **** mời các bạn xem câu tiếp bên dưới **** =====