Câu hỏi:
Có bao nhiêu số phức \(z\) thỏa mãn \(\left( {1 + i} \right)z + \bar z\) là số thuần ảo và \(\left| {z – 2i} \right| = 1\)?
A. 2.
Đáp án chính xác
B. 1.
C. 0.
D. 4.
Trả lời:
Đáp án A
Giả sử \(z = a + bi{\rm{ }}\left( {a,b \in \mathbb{R}} \right)\)
Ta có \(\left| {z – 2i} \right| = 1 \Leftrightarrow \left| {a + \left( {b – 2} \right)i} \right| = 1 \Leftrightarrow \sqrt {{a^2} + {{\left( {b – 2} \right)}^2}} = 1 \Leftrightarrow {a^2} + {\left( {b – 2} \right)^2} = 1.\)
Lại có \(\left( {1 + i} \right)z + \overline z = \left( {1 + i} \right)\left( {a + bi} \right) + a – bi = 2{\rm{a}} – b + ai\) là số thuần ảo.
Nên \(2a – b = 0 \Rightarrow b = 2a \Rightarrow {a^2} + {\left( {2a – 2} \right)^2} = 1 \Leftrightarrow \left[ \begin{array}{l}a = 1\\a = \frac{3}{5}\end{array} \right.\)
+ Với \(a = 1 \Rightarrow b = 2 \Rightarrow z = 1 + 2i\).
+ Với \(a = \frac{3}{5} \Rightarrow b = \frac{6}{5} \Rightarrow z = \frac{3}{5} + \frac{6}{5}i\).
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho a là số thực dương tùy ý và \(a \ne 1.\) Mệnh đề nào dưới đây là đúng?
Câu hỏi:
Cho a là số thực dương tùy ý và \(a \ne 1.\) Mệnh đề nào dưới đây là đúng?
A. \({\log _3}a = {\log _a}3.\)
B. \({\log _3}a = \frac{1}{{{{\log }_3}a}}.\)
C. \({\log _3}a = \frac{1}{{{{\log }_a}3}}.\)
Đáp án chính xác
D. \({\log _3}a = – {\log _a}3.\)
Trả lời:
Đáp án C
Ta có \({\log _3}a = \frac{1}{{{{\log }_a}3}}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Điểm nào trong hình vẽ bên là điểm biểu diễn số phức \(z = – 1 – 2i\)?
Câu hỏi:
Điểm nào trong hình vẽ bên là điểm biểu diễn số phức \(z = – 1 – 2i\)?
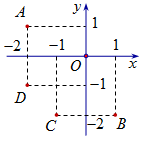
A. Điểm A.
B. Điểm B.
C. Điểm C.
Đáp án chính xác
D. Điểm D.
Trả lời:
Đáp án C
Điểm biểu diễn số phức \(z = – 1 – 2i\) có tọa độ \(\left( { – 1;2} \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho \(\int\limits_0^1 {f\left( x \right)dx} = 2\) và \(\int\limits_1^2 {f\left( x \right)dx} = – 3.\) Tích phân \(\int\limits_0^2 {f\left( x \right)dx} \) bằng
Câu hỏi:
Cho \(\int\limits_0^1 {f\left( x \right)dx} = 2\) và \(\int\limits_1^2 {f\left( x \right)dx} = – 3.\) Tích phân \(\int\limits_0^2 {f\left( x \right)dx} \) bằng
A. 5.
B. \( – 5.\)
C. 1.
D. \( – 1.\)
Đáp án chính xác
Trả lời:
Đáp án D
Ta có \(\int\limits_0^2 {f\left( x \right)d{\rm{x}}} = \int\limits_0^1 {f\left( x \right)d{\rm{x}}} + \int\limits_1^2 {f\left( x \right)d{\rm{x}}} = – 1\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian Oxyz, cho hai điểm \(A\left( {2;3;4} \right),{\rm{ }}B\left( {6;2;2} \right).\) Tìm tọa độ của vectơ \(\overrightarrow {AB} .\)
Câu hỏi:
Trong không gian Oxyz, cho hai điểm \(A\left( {2;3;4} \right),{\rm{ }}B\left( {6;2;2} \right).\) Tìm tọa độ của vectơ \(\overrightarrow {AB} .\)
A. \(\overrightarrow {AB} = \left( {4;3;4} \right).\)
B. \(\overrightarrow {AB} = \left( {4; – 1; – 2} \right).\)
Đáp án chính xác
C. \(\overrightarrow {AB} = \left( { – 2;3;4} \right).\)
D. \(\overrightarrow {AB} = \left( {4; – 1;4} \right).\)
Trả lời:
Đáp án B
Ta có \(\overrightarrow {AB} = \left( {4; – 1; – 2} \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ ?
Câu hỏi:
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ ?
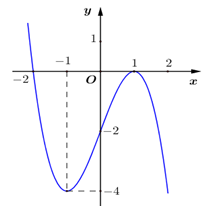
A. \(y = {x^3} – 3{x^2} – 2.\)
B. \(y = {x^3} – 3x – 2.\)
C. \(y = – {x^3} + 3{x^2} – 2.\)
D. \(y = – {x^3} + 3x – 2.\)
Đáp án chính xác
Trả lời:
Đáp án D
Ta có \(y\left( 1 \right) = 0 \Rightarrow \) Loại A và B. Mà \(y\left( { – 1} \right) = – 4\).====== **** mời các bạn xem câu tiếp bên dưới **** =====