Có bao nhiêu số nguyên a để phương trình z2−a−3z+a2+a=0 có hai nghiệm phức z1,z2 thỏa mãn z1+z2=z1−z2.

Câu hỏi:

Có bao nhiêu số nguyên a để phương trình $z^2-\left(a-3\right)z+a^2+a=0$ có hai nghiệm phức $z_1,z_2$ thỏa mãn $\left|z_1+z_2\right|=\left|z_1-z_2\right|$.

A. 4                             

B. 2                             

Đáp án chính xác

C. 3                             

D. 1

Trả lời:

Phương pháp:
– Tính $\Delta$ của phương trình $z^2-\left(a-3\right)z+a^2+a=0$, giải bất phương trình $\Delta <0.$
– Phương trình bậc hai có 2 nghiệm phức thì hai nghiệm đó là số phức liên hợp của nhau, đặt $z_1=x+yi\Rightarrow z_2=x-yi$
– Giải phương trình $\left|z_1+z_2\right|=\left|z_1-z_2\right|$ tìm mối quan hệ giữa x và y.
– Giải phương trình $z^2-\left(a-3\right)z+a^2+a=0$ theo $a,\Delta$ tìm $z_1,z_2.$ Với mỗi trường hợp trên giải phương trình chứa căn tìm
Cách giải:
Xét phương trình $z^2-\left(a-3\right)z+a^2+a=0$ ta có:
$\Delta ={\left(a-3\right)}^2-4\left(a^2+a\right)=-3a^2-10a+9.$
Để phương trình có 2 nghiệm phức thì $-3a^2-10a+9<0\iff \left[\begin{array}{l}a>\frac{-5+2\sqrt{13}}{3}\\ a<\frac{-5-2\sqrt{13}}{3}\end{array}\right.\left(*\right).$
Vì $z_1,z_2$ là hai nghiệm phức của phương trình $z^2-\left(a-3\right)z+a^2+a=0$ nên chúng là 2 số phức liên hợp. Do đó đặt 
Theo bài ra ta có:
$\left|z_1+z_2\right|=\left|z_1-z_2\right|$
$\iff |x + yi + x–yi|=|x + yi – x+yi|$
$\iff \left|2x\right|=\left|2yi\right|$
$\iff \left|x\right|=\left|yi\right|$
$\iff \left|x\right|=\left|y\right|$
$\iff \left[\begin{array}{l}x=y\\ x=-y\end{array}\right.$
Ta có: $z^2-\left(a-3\right)z+a^2+a=0\iff \left[\begin{array}{l}{z}_1=\frac{\left(a-3\right)+\sqrt{\left|\Delta \right|i}}{2}=\frac{a-3}{2}+\frac{\sqrt{\left|\Delta \right|}}{2}i\\ z_1=\frac{\left(a-3\right)-\sqrt{\left|\Delta \right|i}}{2}=\frac{a-3}{2}-\frac{\sqrt{\left|\Delta \right|}}{2}i\end{array}\right.$
TH1: $x=y\Rightarrow a-3=\sqrt{\left|\Delta \right|}\iff \left\{\begin{array}{l}a\ge 3\\ {\left(a-3\right)}^2=3a^2+10a-9\end{array}\right.$
$\iff \left\{\begin{array}{l}a\ge 3\\ 2a^2+16a-18-0\end{array}\right.\iff \left\{\begin{array}{l}a=1\\ a=-9\end{array}\right.\left(ktm\right).$
TH2: $x=-y\Rightarrow 3-a=\sqrt{\left|\Delta \right|}\iff \left\{\begin{array}{l}a\le 3\\ {\left(a-3\right)}^2=3a^2+10a-9\end{array}\right.$
 Hai giá trị này của a thỏa mãn điều kiện (*).
Vậy có 2 số nguyên a thỏa mãn yêu cầu bài toán.
Chọn B.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng AB và B’D’ bằng:
   
   

   Câu hỏi:
   

   Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng AB và B’D’ bằng:

   A. ${30}^0$

   B. ${135}^0$

   C. ${45}^0$

   Đáp án chính xác

   D. ${90}^0$

   Trả lời:

   Phương pháp:
   Sử dụng: $a//a‘\Rightarrow \angle \left(a;b\right)=\angle \left(a‘;b‘\right)$
   Cách giải:
   
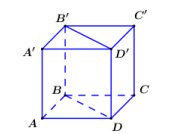
   Ta có B’D’ // BD nên $\angle \left(AB;B‘D‘\right)=\angle \left(AB;BD\right)$
   Vì ABCD là hình vuông nên $\angle ABD={45}^0.$
   Vậy $\angle \left(AB;B‘D‘\right)={45}^0.$
   Chọn C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Biết ∫01fxdx=13 và ∫01gxdx=43. Khi đó ∫01gx−fxdx bằng: 
   
   

   Câu hỏi:
   

   Biết $\underset{0}{\overset{1}{\int }}f\left(x\right)dx=\frac{1}{3}$ và $\underset{0}{\overset{1}{\int }}g\left(x\right)dx=\frac{4}{3}.$ Khi đó $\underset{0}{\overset{1}{\int }}\left(g\left(x\right)-f\left(x\right)\right)dx$ bằng: 

   A. $-\frac{5}{3}$

   B. $\frac{5}{3}$

   C. -1

   D. 1

   Đáp án chính xác

   Trả lời:

   Phương pháp:
   Sử dụng tính chất tích phân: $\underset{a}{\overset{b}{\int }}\left[f\left(x\right)-g\left(x\right)\right]dx=\underset{a}{\overset{b}{\int }}f\left(x\right)dx-\underset{a}{\overset{b}{\int }}g\left(x\right)dx$
   Cách giải:
   $\underset{0}{\overset{1}{\int }}\left[g\left(x\right)-f\left(x\right)\right]dx=\underset{0}{\overset{1}{\int }}g\left(x\right)dx-\underset{0}{\overset{1}{\int }}f\left(x\right)dx=\frac{4}{3}-\frac{1}{3}=1.$
    
   Chọn D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Tập xác định của hàm số y=logx+log3−x là: 
   
   

   Câu hỏi:
   

   Tập xác định của hàm số $y=\log x+\log \left(3-x\right)$ là: 

   A. $\left(3;+\infty \right)$

   B. (0; 3)

   Đáp án chính xác

   C. $\left[3;+\infty \right)$

   D. [1; 3]

   Trả lời:

   Phương pháp:
   Hàm số $y=\log x$ xác định khi x > 0.
   Cách giải:
   Hàm số $y=\log x+\log \left(3-x\right)$ xác định khi $\left\{\begin{array}{l}x>0\\ 3-x>0\end{array}\right.\iff \left\{\begin{array}{l}x>0\\ x<3\end{array}\right.\iff 0<x<3.$
   Chọn B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hàm số y = f(x) có đồ thị như hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
   
   

   Câu hỏi:
   

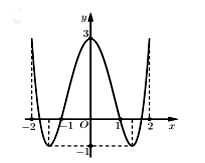
   Cho hàm số y = f(x) có đồ thị như hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
   
   

   A. (0; 1)

   B. (-2; -1)

   C. (-1; 0)

   Đáp án chính xác

   D. (-1; 3)

   Trả lời:

   Phương pháp:
   Dựa vào đồ thị xác định các khoảng đồ thị đi lên từ trái qua phải.
   Cách giải:
   Dựa vào đồ thị và các đáp án ta thấy hàm số y = f(x) đồng biến trên (-1; 0)
   Chọn C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho góc ở đỉnh của một hình nón bằng 600. Gọi r, h, l lần lượt là bán kính đáy, đường cao, đường sinh của hình nón đó. Khẳng định nào sau đây đúng? 
   
   

   Câu hỏi:
   

   Cho góc ở đỉnh của một hình nón bằng ${60}^0.$ Gọi r, h, l lần lượt là bán kính đáy, đường cao, đường sinh của hình nón đó. Khẳng định nào sau đây đúng? 

   A. l = 2r

   Đáp án chính xác

   B. h = 2r

   C. l = r

   D. h = r

   Trả lời:

   Phương pháp:
   – Cho góc ở đỉnh của một hình nón bằng $\alpha$ thì $\tan \frac{\alpha }{2}=\frac{r}{h}$ với r, h lần lượt là bán kính đáy, đường cao của hình nón.
   – Sử dụng công thức: $l^2=h^2+r^2.$
   Cách giải:
   Vì góc ở đỉnh của một hình nón bằng ${60}^0$ nên $\tan {30}^0=\frac{r}{h}\iff \frac{1}{\sqrt{3}}=\frac{r}{h}\iff h=\sqrt{3}r.$
   Lại có $l^2=h^2+r^2\Rightarrow l^2=3r^2+r^2\iff l=2r.$
   Chọn A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====