Câu hỏi:
Cho x,y là các số thực dương thỏa mãn điều kiện
Tính giá trị nhỏ nhất của biểu thức T =x + y.
A.
B.
Đáp án chính xác
C.
D.
Trả lời:
Từ giả thiết ta suy ra
Xét hàm số với
Suy ra y= f( t) là hàm số đồng biến trên R mà từ ( * ) suy ra
f (x+ 2y) =f( xy-1) hay x+ 2y= xy-1
với x>0 suy ra y>1.
Khi đó
Xét hàm số
Vẽ BBT ta thấy với f(y) trên đạt GTNN tại y =
Do đó, giá trị nhỏ nhất của hàm số là .
Vậy kết quả là
Chọn B.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Biết đồ thị hàm số y=2m-nx2+mx+1×2+mx+n-6 (m, n là tham số) nhận trục hoành và trục tung làm hai đường tiệm cận. Tính m+ n
Câu hỏi:
Biết đồ thị hàm số (m, n là tham số) nhận trục hoành và trục tung làm hai đường tiệm cận. Tính m+ n
A. 3
B. 8
C. 9
Đáp án chính xác
D. 10
Trả lời:
+ Ta có
Do đó đường thẳng y= 2m- n là TCN
+ Mà y= 0 là tiệm cận ngang của ĐTHS nên 0 = 2m- n
+ Vì x= 0 là TCĐ của ĐTHS nên x= 0 là nghiệm của phương trình x2+ mx+n- 6= 0
Vậy
Chọn C.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Có bao nhiêu giá trị nguyên của tham số m để phương trình 1+2cosx+1+2sinx=m2 có nghiệm thực?
Câu hỏi:
Có bao nhiêu giá trị nguyên của tham số m để phương trình có nghiệm thực?
A. 3
B. 1
C. 4
Đáp án chính xác
D. 6
Trả lời:
Xét mà suy ra
Ta có:
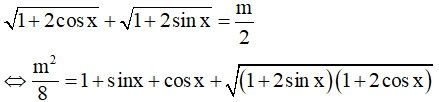
Đặt
Và 2.sinx.cos x= t2– 1
Khi đó: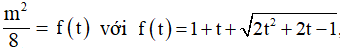
Suy ra y = f( t) là hàm số đồng biến trên
Do đó, để f( t) = m2/8 có nghiệm
Mà m nguyên chọn m= 5; 6;7; 8.
Chọn C.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Xét hàm số fx=x2+ax+b với a, b là tham số. Gọi M là giá trị lớn nhất của hàm số trên [- 1; 3]. Khi M nhận giá trị nhỏ nhất có thể được, tính a.b
Câu hỏi:
Xét hàm số với a, b là tham số. Gọi M là giá trị lớn nhất của hàm số trên [- 1; 3]. Khi M nhận giá trị nhỏ nhất có thể được, tính a.b
A. 2
Đáp án chính xác
B. -3
C. -3/2
D. 2/3
Trả lời:
Ta có
Từ (1) và (2), kết hợp với ta được
Giá trị nhỏ nhất của M là 2 .
Dấu bằng xảy ra khi
cùng dấu
Do đó
Chọn A.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số y=2x+1x+1 có đồ thị (C) . Tìm tất cả các giá trị thực của tham m số sao cho đường thẳng d: y= x+m-1 cắt (C) tại hai điểm phân biệt A; B thỏa mãn AB=23
Câu hỏi:
Cho hàm số có đồ thị (C) . Tìm tất cả các giá trị thực của tham m số sao cho đường thẳng d: y= x+m-1 cắt (C) tại hai điểm phân biệt A; B thỏa mãn
A.
B.
Đáp án chính xác
C.
D.
Trả lời:
Xét phương trình hoành độ giao điểm:
Đường thẳng d cắt (C) tại hai điểm phân biệt khi và chỉ khi phương trình có hai nghiệm phân biệt khác – 1
Khi đó d cắt ( C) tại A( x1; x1+ m- 1) ; B ( x2; x2+ m- 1)
Áp dụng định lý Vi-et ta có:
Vậy
Chọn B.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số y=12+4x-x2x2-6x+2m có đồ thị ( C) . Gọi tập S tất cả các giá trị của tham số thực m để ( C) có đúng hai tiệm cận đứng. Hỏi tập S có bao nhiêu giá trị nguyên
Câu hỏi:
Cho hàm số có đồ thị ( C) . Gọi tập S tất cả các giá trị của tham số thực m để ( C) có đúng hai tiệm cận đứng. Hỏi tập S có bao nhiêu giá trị nguyên
A. 0
B. 1
Đáp án chính xác
C. 3
D. 4
Trả lời:
ĐKXĐ:
Ta có nên để ( C) có hai tiệm cận đứng thì phương trình
có hai nghiệm phân biệt thuộc [ 0; 4]
Đế phương trình có 2 nghiệm phân biệt thì
Gọi 2 nghiệm phân biệt của (*) là x1< x2 ta có 0≤ x1< x2≤ 4.
Theo định lí Vi-et ta có
Khi đó
Kết hợp nghiệm ta có
Mà m nguyên nên m = 4
Chọn B.====== **** mời các bạn xem câu tiếp bên dưới **** =====