Câu hỏi:
Cho tứ diện đều \(ABCD\) có cạnh bằng \(a\). Gọi \(M,{\kern 1pt} {\kern 1pt} N\) lần lượt là trọng tâm các tam giác \(ABD,{\kern 1pt} {\kern 1pt} ABC\) và \(E\) là điểm đối xứng với \(B\) qua \(D\). Mặt \(\left( {MNE} \right)\) chia khối tứ diện \(ABCD\) thành hai khối đa diện trong đó khối đa diện chứa đỉnh \(A\) có thể tích \(V\). Tính \(V\).
A. \(V = \frac{{9\sqrt 2 {a^3}}}{{320}}\).
Đáp án chính xác
B. \(V = \frac{{3\sqrt 2 {a^3}}}{{320}}\).
C. \(V = \frac{{\sqrt 2 {a^3}}}{{96}}\).
D. \(V = \frac{{3\sqrt 2 {a^3}}}{{80}}\).
Trả lời:
Chọn đáp án A
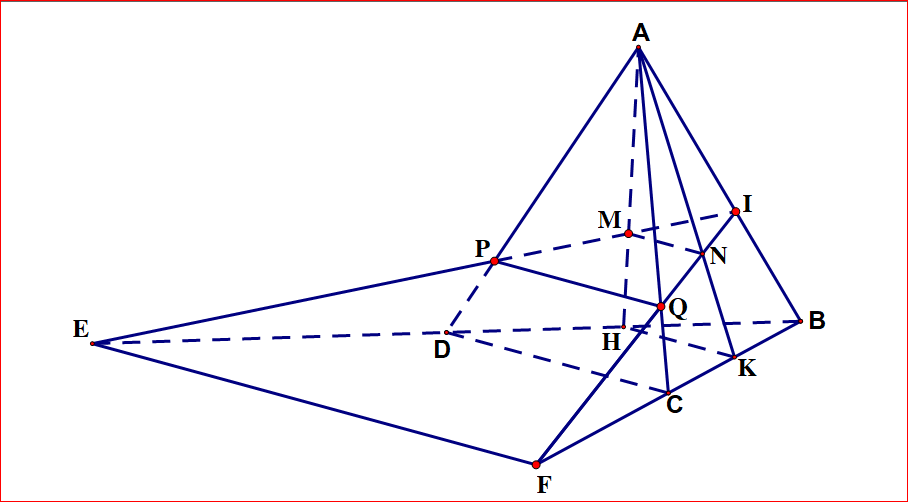
Gọi \(H,{\rm{ }}K\) lần lượt là trung điểm của \(BD,{\rm{ }}BC\) và \(I = EM \cap AB.{\rm{ }}\)Áp dụng định lí Menelaus cho tam giác \(AHB\) ta được \(\frac{{AM}}{{MH}}.\frac{{HE}}{{EB}}.\frac{{BI}}{{IA}} = 1 \Leftrightarrow 2.\frac{3}{4}.\frac{{BI}}{{IA}} = 1 \Leftrightarrow \frac{{BI}}{{IA}} = \frac{2}{3} \Leftrightarrow AI = \frac{3}{5}AB\)
\(\frac{{AI}}{{AB}} = \frac{3}{5} \ne \frac{{AN}}{{AK}} = \frac{2}{3} \Rightarrow \)Hai đường thẳng \(IN\) và \(BC\) cắt nhau, gọi giao điểm là \(F\).
Gọi \(P = EM \cap AD.{\rm{ }}\)Vì \(MN{\rm{//}}CD\) nên áp dụng định lí về giao tuyến của ba mặt phẳng
Ta có \(PQ{\rm{//}}EF{\rm{//}}CD.\)
Áp dụng định lí Menelaus cho tam giác \(ADB\) ta được
\(\frac{{AP}}{{PD}}.\frac{{DE}}{{EB}}.\frac{{BI}}{{IA}} = 1 \Leftrightarrow \frac{{AP}}{{PD}}.\frac{1}{2}.\frac{2}{3} = 1 \Leftrightarrow \frac{{AP}}{{PD}} = 3.\)
Có\(ABCD\) là tứ diện đều cạnh bằng \(a \Rightarrow {V_{ABCD}} = \frac{{{a^3}\sqrt 2 }}{{12}}\)
\(\frac{{{V_{APQI}}}}{{{V_{ABCD}}}} = \frac{{AP}}{{AD}}.\frac{{AQ}}{{AC}}.\frac{{AI}}{{AB}} = \frac{3}{4}.\frac{3}{4}.\frac{3}{5} = \frac{{27}}{{80}} \Rightarrow {V_{APQI}} = \frac{{27}}{{80}}{V_{ABCD}} = \frac{{27}}{{80}}.\frac{{{a^3}\sqrt 2 }}{{12}}.\)
Vậy \({V_{APQI}} = \frac{{9\sqrt 2 {a^3}}}{{320}}\).
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Lớp 12A có 18 học sinh nữ và 17 học sinh nam. Giáo viên Chọn đáp án 1 học sinh trong lớp làm tình nguyện viên tham gia phong trào thanh niên của nhà trường. Hỏi có bao nhiêu cách chọn
Câu hỏi:
Lớp 12A có 18 học sinh nữ và 17 học sinh nam. Giáo viên Chọn đáp án 1 học sinh trong lớp làm tình nguyện viên tham gia phong trào thanh niên của nhà trường. Hỏi có bao nhiêu cách chọn
A.306.
B. 1.
C. 35.
Đáp án chính xác
D. 17.
Trả lời:
Chọn đáp án C
Tổng số học sinh của lớp là \(18 + 17 = 35\).
Số cách chọn 1 học sinh trong lớp là 35 cách.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho cấp số nhân
\(\left( {{u_n}} \right)\) với \({u_1} = \,3\) và \({u_2} = 12\). Công bội của cấp số nhân đã cho bằng
Câu hỏi:
Cho cấp số nhân
\(\left( {{u_n}} \right)\) với \({u_1} = \,3\) và \({u_2} = 12\). Công bội của cấp số nhân đã cho bằngA.4.
Đáp án chính xác
B. 3.
C. 9.
D.\(\frac{1}{4}\).
Trả lời:
Chọn đáp án A
Ta có: \({u_2} = {u_1}.q \Rightarrow q = \frac{{{u_2}}}{{{u_1}}} = \frac{{12}}{3}\, = \,4\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Phương trình \({4^x} – {3.2^x} + 2 = 0\) có nghiệm thuộc khoảng
Câu hỏi:
Phương trình \({4^x} – {3.2^x} + 2 = 0\) có nghiệm thuộc khoảng
A. \(\left( {\frac{1}{2};2} \right)\).
Đáp án chính xác
B. \(\left( {2;4} \right)\).
C.\(\left( { – 1;0} \right)\).
D. \(\left( {3;6} \right)\).
Trả lời:
Chọn đáp án A
\({4^x} – {3.2^x} + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}{2^x} = 1\\{2^x} = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1 \in \left( {\frac{1}{2};2} \right)\end{array} \right.\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Thể tích khối chóp có đường cao bằng \(a\) và diện tích đáy bằng \(2{a^2}\sqrt 3 \) là
Câu hỏi:
Thể tích khối chóp có đường cao bằng \(a\) và diện tích đáy bằng \(2{a^2}\sqrt 3 \) là
A.\(\frac{{2{a^3}\sqrt 3 }}{3}\).
Đáp án chính xác
B.\(\frac{{2{a^3}\sqrt 3 }}{2}\).
C.\(\frac{{2{a^3}}}{3}\).
D.\(\frac{{5{a^3}}}{{\sqrt 3 }}\).
Trả lời:
Chọn đáp án A
Thể tích khối chóp là \(V = \frac{1}{3}.a.2{a^2}\sqrt 3 = \frac{{2{a^3}\sqrt 3 }}{3}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tập xác định của hàm số \(y = {\log _3}\left( {x – 1} \right)\) là
Câu hỏi:
Tập xác định của hàm số \(y = {\log _3}\left( {x – 1} \right)\) là
A. \(\left( {1; + \infty } \right)\).
Đáp án chính xác
B. \(\left[ {1; + \infty } \right)\).
C. \(\left( { – \infty ;1} \right)\).
D.\(\left( {3; + \infty } \right)\).
Trả lời:
Chọn đáp án A
Hàm số \(y = {\log _3}\left( {x – 1} \right)\) có nghĩa khi \(x – 1 >0 \Rightarrow x >1\).
Vậy tập xác định của hàm số \(y = {\log _3}\left( {x – 1} \right)\) là \(\left( {1; + \infty } \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====