Cho số phức z thỏa mãn điều kiện z-1-i+z+1+3i=65. Giá trị lớn nhất của z-2-3i là

Câu hỏi:

Cho số phức z thỏa mãn điều kiện $\left|z–1–i\right|+\left|z+1+3i\right|=6\sqrt{5}$.
Giá trị lớn nhất của $\left|z–2–3i\right|$ là

A. $4\sqrt{5}$

B. $2\sqrt{5}$

C. $6\sqrt{5}$

D. $5\sqrt{5}$

Đáp án chính xác

Trả lời:

Đáp án D
Phương pháp:
– Biểu diễn số phức và giải bài toán tìm GTLN trên mặt phẳng tọa độ.
Cách giải: Gọi I(1;1), J(-1;-3), A(2;3).
Xét số phức , có điểm biểu diễn là M(x;y)
 
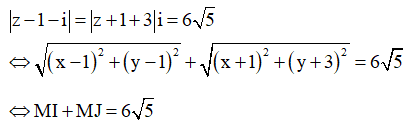
M di chuyển trên đường elip có tiêu điểm I và J, độ dài trục lớn là $3\sqrt{5}$
Tìm giá trị lớn nhất của  tức là tìm độ dài lớn nhất của đoạn AM khi M di chuyển trên elip.
Ta có:

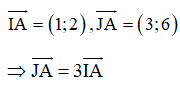
 điểm A nằm trên trục lớn của elip.
AM đạt độ  dài lớn nhất khi và chỉ khi M trùng với B, là đỉnh của elip nằm trên trục lớn và khác phía A so với điểm I.
Gọi S là trung điểm của IJ
S(0;-1) 
Độ dài đoạn AB=SA+SB 
 
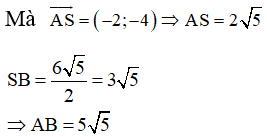
Vậy

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho log3a =2 và log2b=12 . Tính I = 2log3[log3(3a)]+log14b2
   
   

   Câu hỏi:
   

   Cho ${\log }_{3}a =2$ và ${\log }_{2}b=\frac{1}{2}$ . Tính $I = 2{\log }_3\left[{\log }_3\right(3a\left)\right]+{\log }_{\frac{1}{4}}{b}^2$

   A. I = $\frac{–5}{4}$

   B. I = 4

   C. I = 0

   D. I = $\frac{3}{2}$

   Đáp án chính xác

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Rút gọn biểu thức Q = b53: b3 với b > 0
   
   

   Câu hỏi:
   

   Rút gọn biểu thức $Q = b^{\frac{5}{3}}: \sqrt[3]{b}$ với $b > 0$

   A. $Q = b^2$

   B. $Q = b^{\frac{5}{9}}$

   C. $Q = b^{\frac{–4}{3}}$

   D. $Q = b^{\frac{4}{3}}$

   Đáp án chính xác

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Tìm tất cả các giá trị thực của tham số m để hàm số y = log(x2-2x-m+1) có tập xác định là R:
   
   

   Câu hỏi:
   

   Tìm tất cả các giá trị thực của tham số m để hàm số $y = \log (x^2–2x–m+1)$ có tập xác định là R:

   A. $m \ge 0$

   B. m < 0

   Đáp án chính xác

   C. $m \le 2$

   D. m > 2

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Tìm tất cả các giá trị thực của tham số để bất phương trình log22x -2log2x+3m-2 &lt; 0 có nghiệm thực.
   
   

   Câu hỏi:
   

   Tìm tất cả các giá trị thực của tham số để bất phương trình ${\log }_2^{2}x –2{\log }_{2}x+3m–2 < 0$ có nghiệm thực.

   A. m < 1

   Đáp án chính xác

   B. m < $\frac{2}{3}$

   C. m < 0

   D. m $\le 1$

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Với mọi số thực dương a và b thoả mãn a2+ b2=8ab, mệnh đề nào dưới đây đúng?
   
   

   Câu hỏi:
   

   Với mọi số thực dương a và b thoả mãn $a^2+ b^2=8ab$, mệnh đề nào dưới đây đúng?

   

   

   

   Đáp án chính xác

   

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====